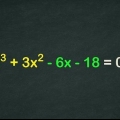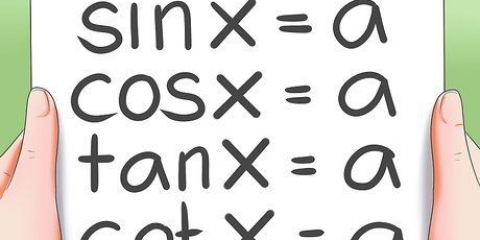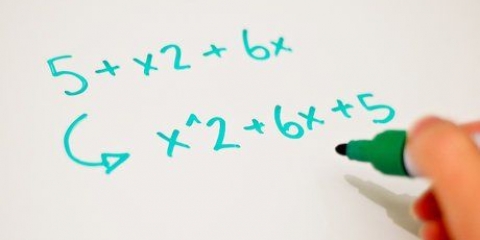Faktorering van vierhoekvergelykings

Inhoud

Trappe
Wenke
Waarskuwings
Benodigdhede

`n Polinoom bevat `n veranderlike (x) verhef tot `n sekere mag, en verskeie terme en/of konstantes. Om `n polinoom te faktoriseer, sal jy die uitdrukking moet afbreek in kleiner uitdrukkings wat met mekaar vermenigvuldig word. Dit vereis wel `n sekere vlak van wiskunde en dit kan dus moeilik wees om te verstaan as jy nog nie so ver is nie.

Trappe

Metode 1 van 7: Aan die gang

Prent getiteld Faktor Tweedegraadse polinome (kwadratiese vergelykings) Stap 1

1. Die vergelyking. Die standaardformaat vir `n kwadratiese vergelyking is:

ax + bx + c = 0
Begin deur die terme in jou vergelyking van hoogste tot laagste mag te orden. Neem byvoorbeeld:

6 + 6x + 13x = 0
Ons gaan hierdie uitdrukking herrangskik om dit makliker te maak om mee te werk – bloot deur die terme rond te skuif:

6x + 13x + 6 = 0

Prent getiteld Faktor Tweedegraadse polinome (kwadratiese vergelykings) Stap 2

2. Vind die faktore deur een van die metodes hieronder te gebruik. Deur die polinoom te faktoriseer sal twee kleiner uitdrukkings tot gevolg hê wat met mekaar vermenigvuldig kan word om die oorspronklike polinoom te kry:

6x + 13x + 6 = (2x + 3)(3x + 2)
In hierdie voorbeeld is (2x +3) en (3x + 2) faktore van die oorspronklike uitdrukking, 6x + 13x + 6.

Prent getiteld Faktor Tweedegraadse polinome (kwadratiese vergelykings) Stap 3

3. Gaan jou werk na! Vermenigvuldig die faktore wat jy gevind het. Kombineer die soortgelyke terme en jy is klaar. Begin met:

(2x + 3)(3x + 2)
Kom ons toets dit deur die terme te vermenigvuldig met EBBL (eerste - buitenste - binne - laaste), wat vir ons gee:

6x + 4x + 9x + 6
Nou tel ons 4x en 9x bymekaar, want dit is gelyke terme. Ons weet die faktore is korrek, want ons kry die vergelyking waarmee ons begin het terug:

6x + 13x + 6

Metode 2 van 7: Proef en Fout

As jy `n redelik eenvoudige polinoom het, kan jy dalk dadelik sien wat die faktore is. Byvoorbeeld, na `n paar oefening, baie wiskundiges in staat is om te sien dat die uitdrukking 4x + 4x + 1 het die faktore (2x + 1) en (2x + 1) net omdat hulle dit al soveel keer gesien het. (Natuurlik sal dit nie so maklik wees met meer ingewikkelde polinome nie.) Kom ons neem `n minder standaard uitdrukking vir hierdie voorbeeld:

3x + 2x - 8

Prent getiteld Faktor Tweedegraadse polinome (kwadratiese vergelykings) Stap 4

1. Skryf die faktore van die neer a termyn en die c termyn. Gebruik die formaat ax + bx + c = 0, erken die a en c terme en let op watter faktore daar is. Vir 3x + 2x - 8 beteken dit:

a = 3 en het 1 paar faktore: 1 * 3
c = -8 en dit het 4 pare faktore: -2 * 4, -4 * 2, -8 * 1, en -1 * 8.

Prent getiteld Faktor Tweedegraadse polinome (kwadratiese vergelykings) Stap 5

2. Skryf twee pare hakies met `n leë spasie. Hier voer jy die konstantes van elke uitdrukking in:

( x ) ( x )

Prent getiteld Faktor Tweedegraadse polinome (kwadratiese vergelykings) Stap 6

3. Vul die spasie voor die x`e met `n paar moontlike faktore van die a waar die. Vir die a term in ons voorbeeld, 3x, is daar net 1 moontlikheid:

(3x)(1x)

Prent getiteld Faktor Tweedegraadse polinome (kwadratiese vergelykings) Stap 7

4. Vul die 2 spasies na die x`e in met `n paar faktore vir die konstantes. Gestel ons kies 8 en 1. Voer hierdie in:

(3x 8)(X 1)

Prent getiteld Faktor Tweedegraadse polinome (kwadratiese vergelykings) Stap 8

5. Bepaal watter tekens (plus of minus) tussen die x-veranderlikes en die getalle geplaas moet word. Afhangende van die tekens van die oorspronklike uitdrukking, is dit moontlik om uit te vind wat die tekens van die konstantes moet wees. Kom ons neem die twee konstantes van die twee faktore h en k om te noem:

As ax + bx + c dan (x + h)(x + k)
As ax - bx - c of ax + bx - c dan (x - h)(x + k)
As ax - bx + c dan (x - h)(x - k)
In ons voorbeeld, 3x + 2x - 8, is die teken:(x - h)(x + k), wat vir ons die volgende twee faktore gee:

(3x + 8) en (x - 1)

Prent getiteld Faktor Tweedegraadse polinome (kwadratiese vergelykings) Stap 9

6. Toets jou keuse met die eerste-buite-binne-laaste vermenigvuldiging. `n Vinnige eerste toets om te sien of die middeltermyn ten minste die regte waarde is. Indien nie, dan het jy waarskynlik die verkeerde een c faktore gekies. Kom ons toets die antwoord:

(3x + 8)(x - 1)
Deur vermenigvuldiging kry ons:

3x - 3x + 8x - 8
Vereenvoudig hierdie uitdrukking deur die soortgelyke terme (-3x) en (8x) by te voeg, en ons kry:

3x - 3x + 8x - 8 = 3x + 5x - 8
Ons weet nou dat ons die verkeerde faktore geneem het:

3x + 5x - 8 3x + 2x - 8

Prent getiteld Faktor Tweedegraadse polinome (kwadratiese vergelykings) Stap 10

7. Ruil jou keuses uit indien nodig. In ons voorbeeld, kom ons probeer 2 en 4, in plaas van 1 en 8:

(3x + 2)(x - 4)
Nou ons c term gelyk aan -8, maar die buitenste/binne produk van (3x * -4) en (2 * x) is -12x en 2x, wat nie die korrekte is nie b term of +2x kry.

-12x + 2x = 10x
10x2x

Prent getiteld Faktor Tweedegraadse polinome (kwadratiese vergelykings) Stap 11

8. Keer die volgorde om indien nodig. Kom ons probeer om 2 en 4 om te draai:

(3x + 4)(x - 2)
Nou ons c term (4 * 2 = 8) en steeds in orde, maar die buitenste/binne produkte is -6x en 4x.Deur hierdie te kombineer kry ons:

-6x + 4x = 2x
2x-2x Ons kom redelik naby aan die 2x waar ons wil wees, maar die teken is nog nie reg nie.

Prent getiteld Faktor Tweedegraadse polinome (kwadratiese vergelykings) Stap 12

9. Gaan jou karakters dubbel na indien nodig. Ons hou hierdie volgorde, maar verwissel dit met die minusteken:

(3x - 4)(x + 2)
Nou die c term steeds ok, en die buitenste/binne produkte is nou (6x) en (-4x). Omdat:

6x - 4x = 2x
2x = 2x Ons sien nou die positiewe 2x terug van die oorspronklike probleem. Dit moet die regte faktore wees.

Metode 3 van 7: Ontbinding

Hierdie metode gee alle moontlike faktore van a en c terme en gebruik dit om uit te vind watter faktore korrek is. As die getalle baie groot is, of die raaiwerk van ander metodes te lank gaan neem, gebruik hierdie manier. N voorbeeld:

6x + 13x + 6

Prent getiteld Faktor Tweedegraadse polinome (kwadratiese vergelykings) Stap 13

1. Vermenigvuldig die a termyn met die c termyn. In hierdie voorbeeld,, a is 6 en c is ook 6.

6 * 6 = 36

Prent getiteld Faktor Tweedegraadse polinome (kwadratiese vergelykings) Stap 14

2. Vind die b term deur faktorisering en toetsing. Ons soek 2 getalle wat faktore is van a * c , en saam die b term (13) vorm.

4 * 9 = 36
4 + 9 = 13

Prent getiteld Faktor Tweedegraadse polinome (kwadratiese vergelykings) Stap 15

3. Vervang die twee getalle wat jy in jou vergelyking kry as die som van die b termyn. Kom ons k en h om die 2 getalle wat ons het, 4 en 9 voor te stel:

ax + kx + hx + c
6x + 4x + 9x + 6

Prent getiteld Faktor Tweedegraadse polinome (kwadratiese vergelykings) Stap 16

4. Faktoreer die polinoom deur te groepeer. Organiseer die vergelyking sodat jy die grootste gemene deler van die eerste twee terme en die laaste twee terme kan isoleer. Beide faktore moet dieselfde wees. Voeg die GCD`s bymekaar en plaas dit tussen hakies, langs die faktore; gevolglik kry jy die twee faktore:

6x + 4x + 9x + 6
2x(3x + 2) + 3(3x + 2)
(2x + 3)(3x + 2)

Metode 4 van 7: Triple Play

Soortgelyk aan die ontbindingsmetode. Die `triple play` metode ondersoek die moontlike faktore van die produk van a en c en gebruik dit om uit te vind wat b moet wees. Neem die vergelyking as `n voorbeeld:

8x + 10x + 2

Prent getiteld Faktor Tweedegraadse polinome (kwadratiese vergelykings) Stap 17

1. Vermenigvuldig die a termyn met die c termyn. Soos met die ontbindingsmetode, gebruik ons dit om die kandidate vir die te bepaal b termyn. In hierdie voorbeeld: a is 8 en c is 2.

8 * 2 = 16

Prent getiteld Faktor Tweedegraadse polinome (kwadratiese vergelykings) Stap 18

2. Vind die 2 getalle met hierdie getal as produk en met `n som gelyk aan die b termyn. Hierdie stap is gelykstaande aan die ontbindingsmetode – ons toets kandidate vir die konstantes. Die produk van die a en c terme is 16, en die c term is 10:

2 * 8 = 16
8 + 2 = 10

Prent getiteld Faktor Tweedegraadse polinome (kwadratiese vergelykings) Stap 19

3. Neem hierdie 2 nommers en vervang hulle in die `triple play`-formule. Neem die 2 nommers van die vorige stap – kom ons plaas dit h en k noem hulle - en plaas hulle in die uitdrukking:

((byl + h)(byl + k))/ a

Hiermee kry ons:

((8x + 8)(8x + 2)) / 8

Prent getiteld Faktor Tweedegraadse polinome (kwadratiese vergelykings) Stap 20

4. Kyk na watter van die twee terme in die noemer heeltemal gedeel kan word a. In hierdie voorbeeld kyk ons of (8x + 8) of (8x + 2) deur 8 gedeel kan word. (8x + 8) is deelbaar deur 8, so ons deel hierdie term deur a en laat ons die ander met rus.

(8x + 8) = 8(x + 1)
Die term wat ons hier gehou het, is die een wat oorgebly het nadat dit deur die gedeel is a term:(x + 1)

Prent getiteld Faktor Tweedegraadse polinome (kwadratiese vergelykings) Stap 21

5. Neem die grootste gemene deler (gcd) van een of albei terme, indien moontlik. In hierdie voorbeeld sien ons dat die tweede term `n gcd van 2 het, want 8x + 2 = 2(4x + 1). Kombineer hierdie antwoord met die term wat jy in die vorige stap ontdek het. Dit is die faktore van jou vergelyking.

2(x + 1)(4x + 1)

Metode 5 van 7: Die verskil tussen twee vierkante

Sommige koëffisiënte in `n polinoom kan herken word as `kwadrate`, of ook as die produk van 2 van dieselfde getalle. Deur uit te vind wat hierdie vierkante is, kan jy dalk die polinome baie vinniger faktoriseer. Ons neem die vergelyking:

27x - 12 = 0

Prent getiteld Faktor Tweedegraadse polinome (kwadratiese vergelykings) Stap 22

1. Verwyder die gcd uit die vergelyking, indien moontlik. In hierdie geval sien ons dat 27 en 12 albei deelbaar is deur 3, so ons kan hulle apart plaas:

27x - 12 = 3(9x - 4)

Prent getiteld Faktor Tweedegraadse polinome (kwadratiese vergelykings) Stap 23

2. Bepaal of die koëffisiënte van jou vergelyking vierkante is. Om hierdie metode te gebruik is dit nodig om die wortel van die terme te kan bepaal. (Let daarop dat ons desimale uitgelaat het - omdat hierdie getalle vierkante is, kan dit die produk van 2 negatiewe getalle wees)

9x = 3x * 3x en 4 = 2 * 2

Prent getiteld Faktor Tweedegraadse polinome (kwadratiese vergelykings) Stap 24

3. Deur die vierkantswortel te gebruik wat jy bepaal het, kan jy nou die faktore uitskryf. Ons neem die a en c waardes van die vorige stap: a = 9 en c = 4, dus die wortels hiervan is: - √a = 3 enc = 2. Dit is die koëffisiënte van die gefaktoriseerde uitdrukkings:

27x - 12 = 3(9x - 4) = 3(3x + 2)(3x - 2)

Metode 6 van 7: Die ABC-formule

As niks blyk te werk nie en jy kan nie die vergelyking faktoriseer nie, gebruik die abc-formule. Neem die volgende voorbeeld:

x + 4x + 1 = 0

Prent getiteld Faktor Tweedegraadse polinome (kwadratiese vergelykings) Stap 25

1. Vul die ooreenstemmende waardes in, in die abc-formule:

x = -b ± √(b - 4ac)
---------------------
2a
Ons kry nou die uitdrukking:

x = -4 ± √(4 - 4•1•1) / 2

Prent getiteld Faktor Tweedegraadse polinome (kwadratiese vergelykings) Stap 26

2. Los op vir x. Jy behoort nou 2 waardes vir x te kry. Hierdie is:

x = -2 + √(3) of x = -2 - √(3)

Prent getiteld Faktor Tweedegraadse polinome (kwadratiese vergelykings) Stap 27

3. Gebruik die waardes van x om die faktore te bepaal. Vul die x-waardes wat in die twee vergelykings verkry is, as konstantes in. Dit is jou faktore. As ons die twee beantwoord h en k dan skryf ons die twee faktore soos volg neer:

(x - h)(x - k)
In hierdie geval is die finale antwoord:

(x - (-2 + √(3))(x - (-2 - √(3)) = (x + 2 - √(3))(x + 2 + √(3))

Metode 7 van 7:Gebruik `n sakrekenaar

As dit toegelaat word (of vereis word) om `n grafiese sakrekenaar te gebruik, maak dit faktorisering baie makliker, veral tydens eksamens en eksamens. Die volgende instruksies is vir `n TI grafiese sakrekenaar. Ons gebruik die vergelyking uit die voorbeeld:

y = x − x − 2

Prent getiteld Faktor Tweedegraadse polinome (kwadratiese vergelykings) Stap 28

1. Tik die vergelyking in jou sakrekenaar in. Jy sal die vergelykingsoplosser gebruik, ook bekend as die [Y = ] skerm.

Prent getiteld Faktor Tweedegraadse polinome (kwadratiese vergelykings) Stap 29

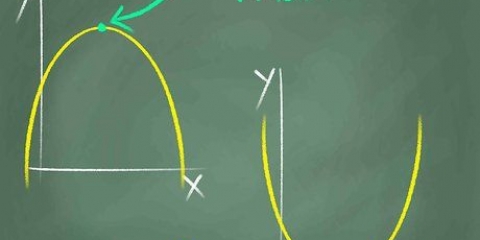
2. Teken die vergelyking met die sakrekenaar. Sodra jy die vergelyking ingevoer het, druk [GRAPH] - jy behoort nou `n geboë lyn te sien, `n parabool as `n grafiese voorstelling van jou vergelyking (en dit is `n parabool, want ons het met `n polinoom te doen).

Prent getiteld Faktor Tweedegraadse polinome (kwadratiese vergelykings) Stap 30

3. Vind waar die parabool met die x-as sny. Aangesien `n kwadratiese vergelyking tradisioneel as ax + bx + c = 0 aangedui word, is dit die twee x-waardes wat die vergelyking gelyk aan nul maak:

(-1, 0), (2, 0)
x = -1, x = 2

As jy nie kan sien waar die parabool met die x-as sny nie, druk [2nd] en dan [TRACE]. Druk [2] of kies "nul". Beweeg die wyser na links van `n kruising en druk [ENTER]. Beweeg die wyser na die regterkant van `n kruising en druk [ENTER]. Beweeg die wyser so na as moontlik aan die kruising en druk [ENTER]. Die sakrekenaar sal die x-waarde aandui.Doen dieselfde vir die ander snypunt.

Prent getiteld Faktor Tweedegraadse polinome (kwadratiese vergelykings) Stap 31

4. Voer die x-waardes wat jy verkry het in die twee gefaktoriseerde uitdrukkings in. As ons die twee x-waardes neem h en k skryf dit as `n term neer, dan lyk die uitdrukking wat ons gebruik so:

(x - h)(x - k) = 0
So ons twee faktore word dan:

(x - (-1))(x - 2) = (x + 1)(x - 2)

Wenke

As jy die polinoom met die abc-formule gefaktoreer het, en jou antwoord bevat wortels, kan jy die x-waardes omskakel na breuke om dit na te gaan.
As `n term geen koëffisiënt voor hom het nie, dan is die koëffisiënt gelyk aan 1, bv. x = 1x.
As jy `n TI-84 sakrekenaar het, is daar `n program genaamd SOLVER wat `n kwadratiese vergelyking vir jou kan oplos. Dit los ook hoërgraad polinome op.
Na baie oefening sal jy dit uiteindelik regkry om polinome uit jou kop op te los. Maar net om seker te maak, is dit beter om dit altyd uit te skryf.
As `n term nie bestaan nie, dan is die koëffisiënt gelyk aan nul. Dan kan dit nuttig wees om die vergelyking te herskryf. Bv. x + 6 = x + 0x + 6.

Waarskuwings

Wanneer jy hierdie konsep in wiskundeklas leer, let op wat die onderwyser verduidelik en moenie net jou eie gunstelingmetode gebruik nie. Jy kan gevra word om `n spesifieke metode op `n toets te gebruik, of grafiese sakrekenaars mag dalk nie toegelaat word nie.