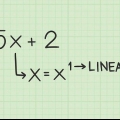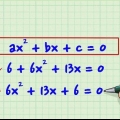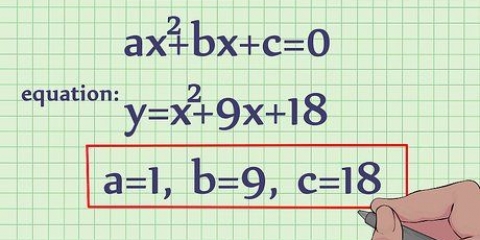Faktoriseer

Inhoud

Trappe
Wenke
Waarskuwings
Benodigdhede

In Algebra is `n kwadratiese vergelyking `n polinoom wat uit 3 terme bestaan, van die vorm ax + bx + c. Polinome het baie toepassings in wiskunde en wetenskap, en die oplossing van kwadratiese vergelykings is `n belangrike vaardigheid. Terwyl die meeste kwadratiese vergelykings eenvoudig in berekening gebring kan word, is daar verskeie gevalle waar `n kwadratiese vergelyking op `n spesiale manier gefaktoreer moet word.As nie een van die metodes in die volgende gids nuttig is nie, kan dit nodig wees om metodes te gebruik vir die faktorisering van hoër polinome.

Trappe

Metode 1 van 4: Afdeling Twee

1. Rangskik die argumente van die kwadratiese vergelyking van grootste na kleinste. `n Argument is een veranderlike in die polinoom; die normale volgorde van plasing van die terme is van hoogste mag tot laagste. Dus, 5 + x + 6x moet as x + 6x + 5 bestel word.

2. Sluit elke faktor uit wat in al drie terme voorkom. As die konstantes van die kwadratiese vergelyking almal veelvoude van dieselfde getal is, dan kan jy hulle buite hakies plaas, of as elke komponent van die kwadratiese vergelyking `n gelyke veranderlike het, dan kan daardie veranderlike buite hakies geplaas word.

Byvoorbeeld, in die kwadratiese vergelyking -8a + 24a + 144, is elke konstante `n veelvoud van 8, dus kan 8 buite hakies geplaas word, wat -8(a - 3a - 18) gee. Al is die koëffisiënt -3 en die konstante -18 albei deelbaar deur -3, is die koëffisiënt 1 van die eerste term nie, so ons kan nie verder faktoriseer nie.

In die kwadratiese vergelyking - x - 2x - 1, is elke term deelbaar deur -1, wat na faktorisering geskryf kan word as (-1)(x + 2x + 1).

3. Soek patrone wat dit makliker maak om `n kwadratiese vergelyking op te los. Vir meer en meer gedetailleerde inligting en voorbeelde, sien die metode om spesiale gevalle van `n kwadratiese vergelyking op te los.

4. Indien enigsins moontlik, probeer om die kwadratiese vergelyking te verdeel in 2 twee terme van die vorm (mx + n)(qx + r). Dit is dikwels net om te probeer wat werk, maar daar is truuks wat dit makliker maak. Kom ons neem eers aan dat die eerste term in die kwadratiese vergelyking (die x-term) gelyk is aan 1 (die term lyk meer soos x as bv., 3x). Die m- en q-waardes van die twee terme is 1, so jou oplossing sal lyk soos (x + b)(x + d). Vind dan vir jou vergelyking van die vorm ax + bx + c, die waardes n en r sodat: n * r = c en n + r = b.

In die voorbeeld, x + 6x + 5, 5 * 1 = 5 en 5 + 1 = 6. Dus, die oplossing is (x + 1)(x + 5).

As nie alle terme in die kwadratiese vergelyking positief is nie, moenie vergeet om die negatiewe getalle te oorweeg nie. Byvoorbeeld, x - 3x - 18 faktor in (x - 6)(x + 3) omdat -6 + 3 = -3 en -6 * 3 = -18.

5. As die konstante in die eerste term nie gelyk is aan 1 nie (bv. as dit meer soos 3x as x lyk), word faktorisering `n bietjie moeiliker, en via ax + bx + c kry jy uiteindelik `n oplossing in die vorm (mx + n)(qx + r). Vir `n korrekte oplossing, m * q = a, m * r + n * q = b, en n * r = c.

Begin deur `n lys te maak van al die moontlike faktore van a en c. Kontroleer dan watter paar faktore werk, deur gebruik te maak van die beperkings soos hierbo aangedui.

Neem byvoorbeeld 3x + 10x + 8. Moontlike faktorpare van 3 is 1 * 3. Moontlike faktorpare van 8 is 1 * 8 en 2 * 4. Aangesien 3 * 1 = 3 (die term van die kwadratiese vergelyking), 1 * 4 + 2 * 3= 10 (die b-term), en 2 * 4 = 8 (die c-term), is die oplossing (3x + 4) (x + 2).

Metode 2 van 4: Faktorering van spesiale gevalle

1. Kyk of die konstante in die eerste term of die derde term van die vergelyking priem is. ’n Priemgetal is slegs deur homself en 1 deelbaar. Dit verminder die aantal moontlike binomiale faktore. In die vorige voorbeeld: x + 6x + 5 is daar net 1 moontlike stel binomiale faktore, (x + 5)(x + 1), want 5 is priem.

2. Kyk of die kwadratiese vergelyking `n perfekte vierkant is. Dit vereis dat die waardes van die koëffisiënte a en c van die vergelyking ax + bx + c perfekte vierkante is (en positief!), en dat die waarde van b dubbel die waarde van die produk van die vierkantswortel van a en c is.

(x + a) word x + 2ax + a. Byvoorbeeld, (x + 3) = x + 6x + 9, en (3x + 2) = 9x + 12x + 4.

Net so word (x - a) x - 2ax + a. Byvoorbeeld, (x - 3) = x - 6x + 9.

3. Vir sommige kwadratiese vergelykings van die vorm x - n:

(x + a)(x - a) word x - a. Dus kan x - 9 vinnig in bereken word in (x + 3)(x - 3), en 4x - 4 = (2x + 2)(2x - 2).

Metode 3 van 4: Gebruik die abc-formule

Vir kwadratiese vergelykings van die vorm ax + bx + c wat moeilik of onmoontlik is om op te los, gebruik die abc-formule.

1. Leer om die abc-formule te gebruik.

2. Tik a, b en c in en los die eerste deel van die formule op. Gestel ons het die kwadratiese vergelyking x + 5x + 6.

Begin met b - 4ac, wat 5 - 4(1)(6) = 1 is. Die vierkantswortel van 1 is 1.

Voltooi deur die vergelyking op te los. -b + 1 = -5 + 1 = -4. Deel dit deur 2a (2 * 1 = 2) om -2 as `n antwoord te kry.

3. Los die ander deel op. Ons weet reeds dat die vierkantswortel van b - 4ac = 1. -b - 1 = -6. Deel dit deur 2a (2) om -3 te kry.

4. Kontroleer jou oplossings deur hulle vir x in te vul. Soms is een of meer van die antwoorde nie geldige oplossings nie (byvoorbeeld, as dit denkbeeldige getalle is). Maar as `n kwadratiese vergelyking `n oplossing het, dan sal die vergelyking dit vind.

Let daarop dat as ons hierdie vergelyking in berekening gebring het, in plaas daarvan om die abc-formule te gebruik, ons as antwoord (x + 2)(x + 3) sou gehad het. As jy hierdie vergelyking gelyk aan 0 stel, kry jy twee oplossings, x = 2 en x = -3, wat ons ook met die formule gevind het.

Metode 4 van 4: Die versteekte vierkant in `n polinoom

Sommige kwadratiese vergelykings is van `n hoër orde, maar in wese net kwadraties. Sodra dit as sodanig erken is, kan jy hulle as sodanig behandel deur vervanging te gebruik.

1. Kyk na die veranderlikes in elke kwartaal.Byvoorbeeld, x - 7x + 12 blyk `n mag van 6 te wees, maar na vervanging van u=x word dit u - 7u + 12. Dit laat jou met `n vergelyking wat baie makliker is om op te los.

Meer komplekse vervangings kan help om moeiliker probleme op te los. Byvoorbeeld, xy - 7xy + 12y word vereenvoudig na xy(u - 7u + 12) en na vervanging u = x/y. So `n vervanging is moontlik wanneer die som van die magte van die twee terme twee keer die mag van die oorblywende term is.

2. As so `n substitusie kan plaasvind, faktoreer dan die eenvoudige polinoom uit, in hierdie geval, u - 7u + 12 = (u-3)(u-4)

3. Maak die vervanging ongedaan en pas x op die oplossing toe. Dus, vervang u met x , x - 7x + 12 = (x - 3)(x - 4). Indien moontlik of verlang, kan elke faktor selfs meer vereenvoudig word.

Wenke

Gebruik Eisenstein se kriterium om vinnig te bepaal of `n polinoom nie-reduceerbaar en nie-faktoreerbaar is. Hierdie maatstaf geld vir enige polinoom, maar veral vir `n kwadratiese vergelyking. As daar `n priemgetal p is wat die laaste twee terme deelbaar maak en aan die volgende voorwaardes voldoen, kan die polinoom nie verminder word nie:

Die konstante term (die c in `n kwadratiese vergelyking van die vorm ax + bx + c) is `n meervoud van p maar nie van p nie.
Die eerste term (hier, a) is nie `n meervoud van p.
Byvoorbeeld, 14x + 45x + 51 is onherleibaar omdat dit `n priemgetal (3) het wat beide 45 en 51 deelbaar maak, maar nie 14 en 51 nie, wat nie deelbaar is deur 3 nie.

Jy kan polinome van veelvuldige veranderlikes faktoriseer deur die bogenoemde metodes te gebruik as dit kwadratiese vergelykings is wat een of ander veranderlike aanvaar. Neem byvoorbeeld 4xy - 5x + 15y. Dit kan herskryf word as (4x)y + 15y - 5x. Let daarop dat dit pas by die vorm ax + bx + c, waar a = 4x en c = 5x. Hierdie vergelyking kan dan met die abc-formule opgelos word.

Jy kan faktorisering van kwadratiese vergelykings oefen deur probleme te doen in `n boek wat oor algebra handel.

Waarskuwings

Alhoewel dit waar is vir vierkante, is kwadratiese vergelykings wat in berekening gebring kan word nie noodwendig die produk van twee binaries nie. `n Teenvoorbeeld is x + 105x + 46 = (x + 5x + 2)(x - 5x + 23).