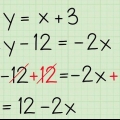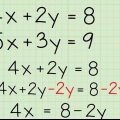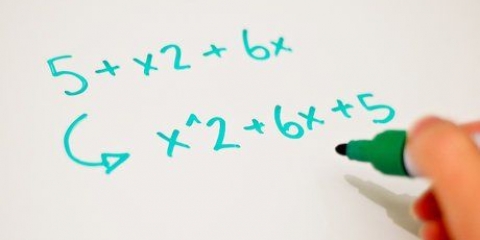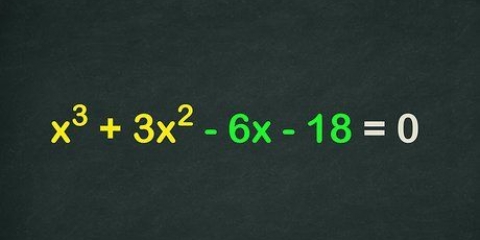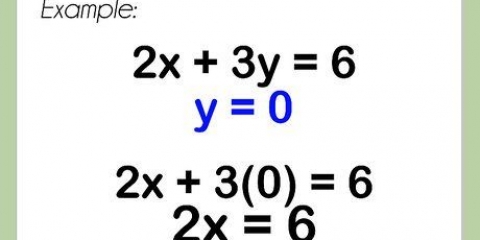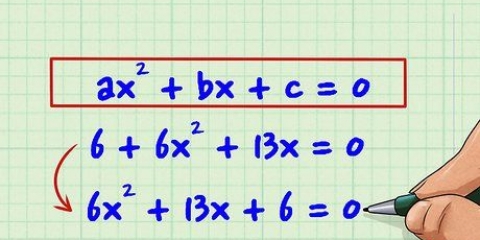Byvoorbeeld, die veranderlike 12y kan herskryf word as die produk van die faktore van 12 en y. Ons kan 12y skryf as 3(4y), 2(6y), ens., gebruik die faktore van 12 wat die gerieflikste is. Ons kan selfs so ver as 12j gaan verskeie kere ontbind. Met ander woorde, ons hoef nie by 3(4y) of 2(6y) te stop nie - ons kan 4y en 6y in 3(2(2y) en 2(3(2y) onderskeidelik inreken). Blykbaar is hierdie twee uitdrukkings gelykstaande aan mekaar. 
Kom ons probeer `n voorbeeldprobleem. Om die vergelyking 12x + 6 te faktoriseer, soek ons eers die gcd van 12x en 6. 6 is die grootste getal wat beide 12x en 6 verdeel, dus kan ons die vergelyking vereenvoudig tot 6(2x + 1). Hierdie proses is ook van toepassing op vergelykings wat negatiewe getalle en breuke behels. x/2 + 4, byvoorbeeld, kan vereenvoudig word tot 1/2(x + 8) en -7x + -21 kan in -7(x + 3) in berekening gebring word. 

Neem byvoorbeeld die kwadratiese vergelyking x + 5x + 6 = 0. Aangesien 3 x 2 = 6 en 3 + 2 = 5, word die vereenvoudigde vergelyking (x + 3)(x + 2). Geringe variasies op hierdie eenvoudige kitsoplossing kan gevind word in die vergelyking self: As die kwadratiese vergelyking in die vorm x-bx+c is, sal jou antwoord soos volg lyk: (x - _)(x - _). As van die vorm x+bx+c, dan sal jou antwoord soos volg lyk: (x + _)(x + _). Indien van die vorm x-bx-c, sal jou antwoord soos volg lyk: (x + _)(x - _). Let wel: Die spasies kan breuke of desimale wees. Byvoorbeeld, die vergelyking x + (21/2)x + 5 = 0 faktore in (x + 10)(x + 1/2). 
Kom ons werk `n voorbeeldopdrag uit. 3x - 8x + 4 lyk aanvanklik `n bietjie intimiderend. Maar as ons besef dat 3 net twee faktore het (3 en 1), dan word dit baie makliker, want ons weet dat ons antwoord in die vorm moet wees (3x +/- _)(x +/- _). In hierdie geval sal die korrekte antwoord gee deur -2 in die spasies in te voer. -2 × 3x = -6x en -2 × x = -2x. -6x + -2x = -8x. -2 × -2 = 4, dus sien ons dat die terme wat tussen hakies vermenigvuldig word, die oorspronklike vergelyking as die produk het. 
Byvoorbeeld, die vergelyking x + 6x + 9 voldoen aan hierdie vorm. 3 is 9 en 3 × 2 is 6. Ons weet dus dat die faktore van hierdie vergelyking gelyk is aan (x + 3)(x + 3) of (x + 3). 
Kom ons keer terug na die vergelyking x + 5x + 6 = 0. Die vergelyking wat opgelos is, is (x + 3)(x + 2) = 0. As een van hierdie faktore gelyk is aan 0, dan is die hele vergelyking 0, dus die moontlike antwoorde vir x is daardie getalle waar (x + 3) en (x + 2) gelyk is aan 0. Hierdie getalle is -3 en -2 onderskeidelik. 
Ons pas -2 en -3 toe op x + 5x + 6 = 0. Eerstens: -2: (-2) + 5(-2) + 6 = 0 4 + -10 + 6 = 0 0 = 0. Dit is korrek, so -2 is `n geldige antwoord. Nou probeer ons -3: (-3) + 5(-3) + 6 = 0 9 + -15 + 6 = 0 0 = 0. Dit is ook korrek, so -3 is ook `n geldige antwoord. 

Die vergelyking 4x + 8xy + 4y kan herskryf word as 4x + (2 × 2 × 2)xy + 4y. Nou word dit duidelik dat dit in die korrekte vorm is, sodat ons met `n mate van vertroue kan stel dat ons vergelyking in (2x + 2y) verreken kan word. 
Byvoorbeeld: 8x - 27y kan in berekening gebring word in (2x - 3y)(4x + ((2x)(3y)) + 9y).
Faktoreringsvergelykings
Inhoud
In wiskunde is dit faktoriseer die bepaling van getalle of uitdrukkings wat, wanneer met mekaar vermenigvuldig, `n bepaalde waarde of vergelyking oplewer. Faktorering is `n nuttige vaardigheid om aan te leer wanneer eenvoudige wiskundeprobleme opgelos word; die vermoë om korrek te faktoriseer word byna noodsaaklik wanneer ons met kwadratiese vergelykings en ander polinome handel. Faktorering kan gebruik word om eenvoudige wiskundige vergelykings te vereenvoudig om die oplossing daarvan makliker te maak. Faktorering kan jou toelaat om moontlike antwoorde self baie vinniger uit te sluit as wanneer jy elkeen van hulle moes nagaan.
Trappe
Metode 1 van 3: Faktorering van getalle en eenvoudige vergelykings

1. Verstaan die definisie van faktorisering in getalle. Faktorering is in beginsel eenvoudig, maar in die praktyk kan dit nogal uitdagend wees wanneer komplekse vergelykings opgelos word. Daarom is die eenvoudigste benadering om met klein getalle en dan eenvoudige vergelykings te begin voordat jy na meer gevorderde toepassings beweeg. Die faktore van `n gegewe getal is die getalle wat, saam vermenigvuldig, daardie enkele getal oplewer. Byvoorbeeld, die faktore van 12 is 1, 12, 2, 6, 3 en 4, want 1 × 12, 2 × 6 en 3 × 4 het almal 12 as hul produk.
- Nog `n manier om hieroor te dink, is dat die faktore van `n gegewe getal daardie getalle is wat die getal in maak kan in sy geheel gedeel word.
- Kan jy al die faktore van 60 vind? Ons gebruik die getal 60 vir verskeie toepassings (die aantal minute in `n uur, sekondes in `n minuut, ens.) want dit is deelbaar deur `n groot stel getalle.
- Die faktore van 60 is 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 en 60.

2. Verstaan dat vergelykings ook in berekening gebring kan word. Net soos getalle kan veranderlikes met koëffisiënte ook in berekening gebring word. Jy doen dit deur die faktore van die koëffisiënt van die veranderlike te vind. Om te weet hoe om veranderlikes te faktoriseer, is nuttig om vergelykings waarvan die veranderlikes deel is te vereenvoudig.

3. Pas die distributiewe eienskap van vermenigvuldiging toe op faktorisering van wiskundige vergelykings. Deur jou kennis te gebruik van hoe om beide gereelde getalle en veranderlikes met koëffisiënte te faktoriseer, kan jy ook wiskundige vergelykings vereenvoudig deur die faktore wat gemeen is aan getalle en veranderlikes in `n wiskundige vergelyking te bepaal. Gewoonlik sal ons die vergelyking so ver as moontlik vereenvoudig deur te soek na die grootste gemene deler (gcd). Hierdie vereenvoudigingsproses is moontlik as gevolg van die distributiewe eienskap van vermenigvuldiging, wat bepaal dat vir enige getal a, b en c, a(b + c) = ab + ac.
Metode 2 van 3: Faktorering van kwadratiese vergelykings

1. Maak seker dat die vergelyking in kwadratiese vorm is (ax + bx + c = 0). kwadratiese vergelykings is van die vorm ax + bx + c = 0, waar a, b en c numeriese konstantes is en a nie gelyk aan 0 is nie (let op dat a gelyk is aan kan is op 1 of -1). As jy te doen het met `n vergelyking met een veranderlike (x) en een of meer terme van x kwadraat, kan jy gewoonlik die terme van die vergelyking omruil deur `n standaard wiskundige bewerking te gebruik om 0 aan die een kant van die vergelyking te kry. kry die gelyke teken en byl, ens. aan die ander kant.
- Byvoorbeeld, jy het die volgende wiskundige vergelyking: 5x + 7x - 9 = 4x + x - 18 wat vereenvoudig kan word na x + 6x + 9 = 0, in die kwadratiese vorm.
- Vergelykings met groter magte van x, soos x, x, ens. is nie kwadratiese vergelykings nie. Dit is kubieke vergelykings of hoër, tensy die vergelyking vereenvoudig kan word sodat die terme met hoër magte van x(as vierkante) uitgeskakel word.

2. In kwadratiese vergelykings waar a = 1, faktoriseer jy in (x+d )(x+e), waar d × e = c en d + e = b. As jou kwadratiese vergelyking in die vorm x + bx + c = 0 is (met ander woorde, as die koëffisiënt van x = 1), dan is dit moontlik (maar nie seker nie) dat `n relatief eenvoudige kortpad gebruik kan word om die vergelyking te faktoriseer. Soek twee getalle wat albei c as `n produk het en tel hulle bymekaar om b as `n som te kry. As jy hierdie twee getalle d en e het, plaas hulle in die volgende uitdrukking: (x+d)(x+e). Hierdie twee terme, wanneer vermenigvuldig, gee jou die kwadratiese vergelyking - met ander woorde, hulle is die faktore van jou kwadratiese vergelyking.

3. Indien moontlik kan jy ook die faktore oplos deur net mooi te kyk. Glo dit of nie, jy kan eenvoudige kwadratiese vergelykings oplos net deur noukeurig na die probleem te kyk en dan die moontlike antwoorde te weeg totdat jy die regte een kry. Met ander woorde, ontbind in faktore deur uit te probeer. As die vergelyking van die vorm ax+bx+c en a is>1, dan sal die terme van die vorm (dx +/- _)(ex +/- _) wees, waar d en e konstantes is, groter as nul, wat saam vermenigvuldig het a as die produk. Beide d en e (of albei) kan gelyk aan 1, maar dit is nie altyd so nie. As albei 1 is, dan het jy in wese die vinnige metode wat hierbo beskryf is, gebruik.

4. Los dit op deur kwadratering. In sommige gevalle kan kwadratiese vergelykings vinnig en maklik in berekening gebring word deur `n spesiale wiskundige eienskap te gebruik. Enige kwadratiese vergelyking van die vorm x + 2xh + h = (x + h). So as in jou vergelyking die waarde vir b twee keer dié van die vierkantswortel van c is, dan kan jou vergelyking verreken word in (x + (sqrt(c))).

5. Gebruik faktore om kwadratiese vergelykings op te los. Ongeag hoe jy `n kwadratiese vergelyking faktoriseer; sodra dit ingereken is, kan jy die moontlike antwoorde vir die waarde vir x vind deur elke faktor gelyk aan nul te stel en daarvoor op te los. Aangesien jy op soek is na waardes vir x waar jou vergelyking nul is, sal `n waarde vir x wat enige faktor gelyk aan nul maak die moontlike antwoord van jou kwadratiese vergelyking wees.

6. Kontroleer jou antwoorde – sommige van hulle kan verkeerd wees! Sodra jy die moontlike antwoorde vir x gevind het, pas dit terug op jou oorspronklike vergelyking om te sien of hulle geldig is. Soms is die antwoorde wat jy kry die oorspronklike vergelyking nie maak gelyk aan nul wanneer jy dit toepas. Hierdie antwoorde is verkeerd en ons ignoreer hulle.
Metode 3 van 3: Faktorering van ander vorme van vergelykings

1. As die vergelyking van die vorm a-b is, dan is die gefaktoriseerde terme (a+b)(a-b). Vergelykings van twee veranderlikes word anders opgelos as kwadratiese vergelykings. Vir enige vergelyking a-b waar a en b nie gelyk is aan 0 nie, is die faktore van die vergelyking (a+b)(a-b).
- Byvoorbeeld, die vergelyking 9x - 4y = (3x + 2y)(3x - 2y).

2. As die vergelyking die vorm a+2ab+b het, ontbind dit in (a+b). Let wel: met a die drieterm van die vorm a-2ab+b, die opgeloste vorm verskil effens: (a-b).

3. As die vergelyking van die vorm a-b is, dan ontbind jy dit in (a-b)(a+ab+b). Ten slotte moet genoem word dat kubieke vergelykings en hoër polinome ook in berekening gebring kan word, hoewel hierdie proses vinnig onwerkbaar ingewikkeld raak.
Wenke
- a-b kan in berekening gebring word, maar a+b kan nie.
- Leer hoe om konstantes te faktoriseer – dit kan help.
- Pasop vir breuke tydens faktorisering en werk dit korrek en versigtig uit.
- As jy `n drieterm van die vorm x+bx+ (b/2) het, dan is die gefaktoriseerde vorm (x+(b/2)) (jy kan dit met `n vierkantsformule teëkom).
- Onthou dat a x 0 = 0.
Benodigdhede
- Papier
- Potlood
- Wiskunde boek (indien nodig)
Artikels oor die onderwerp "Faktoreringsvergelykings"
Оцените, пожалуйста статью
Soortgelyk
Gewilde