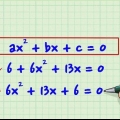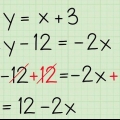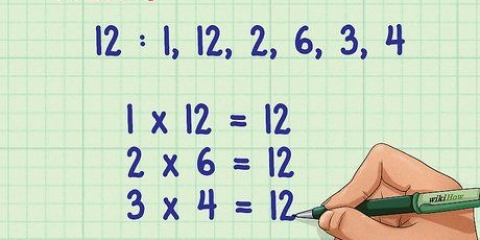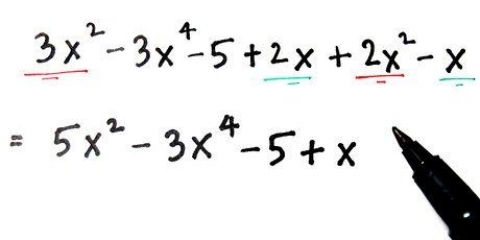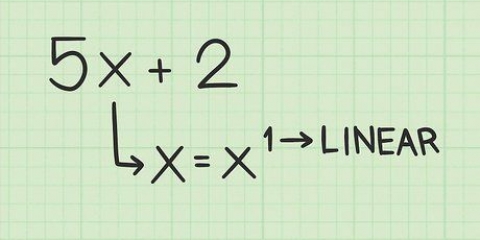By (x + 3x), sien ons dat x gelyk is. By (-6x - 18), sien ons dat -6 gelyk is. 
Deur x te faktoreer kry ons x(x + 3). Deur -6 uit die tweede stuk te ontbind kry ons -6(x + 3). 
Dit gee (x + 3)(x - 6). 
Die oplossings is -3, en √6. 

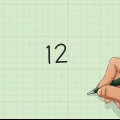
Faktore is die getalle wat jy saam kan vermenigvuldig om `n ander getal te kry. In hierdie geval is dit die faktore van 10, of "d": 1, 2, 5 en 10. 
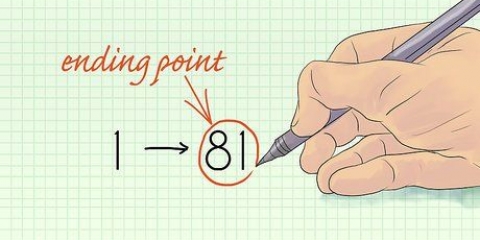
Begin deur die eerste faktor, 1, te gebruik. plaasvervanger "1" vir elke "X" in die vergelyking:
(1) - 4(1) - 7(1) + 10 = 0 Dit gee: 1 - 4 - 7 + 10 = 0. Aangesien 0 = 0 `n ware stelling is, weet jy dat x = 1 die oplossing is. 
"x = 1" is dieselfde as "x - 1 = 0" of "(x - 1)". Jy het net een "1" van elke kant van die vergelyking afgetrek. 
Kan jy (x - 1) van x faktoriseer? Nee dit is nie moontlik nie. Maar as jy eers `n -x van die tweede veranderlike leen: x(x - 1) = x - x. Kan jy faktor (x - 1) van wat oorbly van die tweede veranderlike? Nee, dit is ook nie hier moontlik nie. Jy moet weer iets van die derde veranderlike leen, wat 3x van -7x is. Dit gee ons -3x(x - 1) = -3x + 3x. Aangesien jy 3x uit -7x geneem het, is die derde veranderlike nou -10x en die konstante is 10. Kan jy dit losmaak. Ja natuurlik! -10(x - 1) = -10x + 10. Wat jy gedoen het, is om die veranderlikes te herrangskik sodat jy die faktor (x - 1) uit die hele vergelyking kan kry. Die gewysigde vergelyking lyk soos volg: x - x - 3x + 3x - 10x + 10 = 0, maar is steeds dieselfde as x - 4x - 7x + 10 = 0. 
x(x - 1) - 3x(x - 1) - 10(x - 1) = 0. Jy kan dit herrangskik om dit makliker te maak om weer op te los: (x - 1)(x - 3x - 10) = 0. Hier probeer jy net faktoriseer (x - 3x - 10). Die faktore word dan (x + 2)(x - 5). 
(x - 1)(x + 2)(x - 5) = 0 Dit gee die oplossings vir 1, -2 en 5. Voeg -2 in die vergelyking in: (-2) - 4(-2) - 7(-2) + 10 = -8 - 16 + 14 + 10 = 0. Voeg 5 in die vergelyking in: (5) - 4(5) - 7(5) + 10 = 125 - 100 - 35 + 10 = 0.
Faktorering van 'n derdegraadse polinoom
Inhoud
Hierdie artikel handel oor faktorisering van `n kubieke polinoom, ook genoem `n polinoom. Ons gaan ondersoek hoe ons dit kan doen deur groepering te gebruik en die faktore van die vrye term te gebruik.
Trappe
Deel 1 van 2: Ontbind deur groepering

1. Verdeel die polinoom in twee groepe. Die verdeling van die polinoom help om elke individuele deel op te los.
- Gestel ons werk met die volgende polinoom:" x + 3x - 6x - 18 = 0. Kom ons verdeel dit in (x + 3x) en (-6x - 18)

2. Probeer om uit te vind wat dieselfde is in elke groep.

3. Verwyder hierdie gelyke faktore uit die twee terme.

4. As elk van die twee terme dieselfde faktor bevat, kan jy hierdie faktore kombineer.

5. Vind die oplossing deur na die wortels te kyk. As jy x in `n vierkantswortel het, onthou dat beide positiewe en negatiewe getalle vir daardie vergelyking geldig is.
Deel 2 van 2: Faktorering met die vrye termyn

1. Herrangskik die uitdrukking in die volgende vorm: byl+bx+cx+d.
- Gestel jy werk met die vergelyking: x - 4x - 7x + 10 = 0.

2. Vind alle faktore van "d". Die konstante "d" word die getal met geen veranderlikes langsaan soos "X".

3. Vind `n faktor wat die polinoom gelyk aan nul maak. Ons wil bepaal watter faktor die polinoom gelyk aan nul maak as ons hierdie faktor toepas vir "X" vul die vergelyking in.
(1) - 4(1) - 7(1) + 10 = 0

4. Gaan herrangskik nou alles. As x=1 dan is dit moontlik om hierdie vergelyking effens anders te skryf sonder om die betekenis te verander.

5. Faktoreer die vierkantswortel van die vergelyking. "(x - 1)" is die wortel. Probeer om dit uit die res van die vergelyking te faktoriseer. Doen dit met een polinoom op `n slag.

6. Gaan voort om die faktore van die vrye termyn te vervang. Kyk na die getalle wat jy met (x - 1) in Stap 5 opgelos het:

7. Jou oplossing is die gefaktoriseerde wortels. Kontroleer hierdie oplossing deur elkeen van hulle terug in die oorspronklike vergelyking in te voeg.
Wenke
- Die kubieke vergelyking is die produk van 3 eerstegraadsvergelykings of van `n eerstegraadsvergelyking en `n tweedegraadsvergelyking wat nie in berekening gebring kan word nie. In laasgenoemde geval, nadat jy die eerstegraadse polinoom gevind het, gebruik jy langdeling om die tweedegraadse polinoom te vind.
- Daar is geen kubieke polinome wat nie in berekening gebring kan word wanneer dit by reële getalle kom nie, want hierdie vergelyking moet `n vierkantswortel van reële getalle hê. Derdegraadsvergelykings soos x + x + 1 wat `n irrasionale reële wortel het, kan nie in polinome verreken word met heelgetalle of rasionale getalle as koëffisiënt. Alhoewel dit in die vergelyking self ingereken kan word, kan dit nie tot `n heelgetalpolinoom gereduseer word nie.
Metode 2 kom neer op langdeling van twee polinome, a.v:
(x-1) ∕x³ - 4x²-7x+10 ∕
- x³ - 1x².................................= (x-1) (x²)
- - 3x²-7x
- 3x²+ 3x.........................= (x-1) (-3x)
- - 10x + 10
- 10x + 10................= (x-1) (-10)
- 0............................ x²- 3x-10 (kwosiënt)
Bepalings x², -3x en -10 van die kwosiënt word verkry deur altyd die 1ste term van die deler ( x ) af te trek van die eerste term van die dividend, of wat daarvan oorbly ( x³, -3x², -10x ).
Artikels oor die onderwerp "Faktorering van 'n derdegraadse polinoom"
Оцените, пожалуйста статью
Gewilde