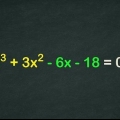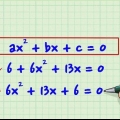→
→ 
 →
→ 
 →
→ 
Let op hoe die minustekens voor die 2 bly. Wanneer `n term afgetrek word, bly die minusteken voor dit. 
Oefenopdrag: .
. Faktore van 3:1, 3 Faktore van 6: 1, 2, 3, 6. `Die grootste gemene deler is 3`. 
Oefenopdrag: .
. Vind die grootste gemene delers: 3 Om faktor uit beide terme te verwyder:

Oefenopdrag:
Vind die grootste gemene delers: 3 Om faktor uit beide terme te verwyder:
Vermenigvuldig faktor met nuwe uitdrukking:
Finale opgeloste antwoord: 

Om terme te herrangskik:
Vind die grootste gemeenskaplike verdeler:
Om faktor uit beide terme te verwyder:
Vermenigvuldig faktor met nuwe uitdrukking:
Kontroleer antwoord:


Oefenopdrag:
Gelyk aan nul:


Oefenopdrag:
Gelyk aan nul:
Los op:

Oefenopdrag:
Gelyk aan nul:
Los op:
Maak beide terme gelyk aan nul 0: 




y = 0 

y = 4 


 Hierdie antwoord is korrek
Hierdie antwoord is korrek

 Hierdie antwoord is ook korrek.
Hierdie antwoord is ook korrek.

Oorspronklike opdrag:
Om terme te herrangskik:
Om soortgelyke terme saam te voeg:
Vind die grootste gemene delers:
Los op:

Die formule vir die verskil van perfekte vierkante:
Oefenopdrag:
Bepaal die vierkantswortels: 

Pas vierkantswortels toe op formule: 

Formule vir die verskil van derde magte:
Oefenopdrag:
Bepaal die kubuswortels: ![Faktorering van binomiale {sqrt[ {3}]{8x^{3}}}=2x](https://wikimedia.org/api/rest_v1/media/math/render/svg/77ed49f7f0ab2dfb9de3438ac123641fb683a0a0)
![Faktorering van binomiale {sqrt[ {3}]{27}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca5392df17ff31f62e3cae649d51dd36bde856ce)
Pas blokkies toe op die formule: 

Formule vir die som van perfekte kubusse:
Oefenopdrag:
Bepaal die kubuswortels: ![Faktorering van binomiale {sqrt[ {3}]{8x^{3}}}=2x](https://wikimedia.org/api/rest_v1/media/math/render/svg/77ed49f7f0ab2dfb9de3438ac123641fb683a0a0)
![Faktorering van binomiale {sqrt[ {3}]{27}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca5392df17ff31f62e3cae649d51dd36bde856ce)
Pas die blokkies toe op die formule: 
Faktorering van binomiale
Inhoud
In algebra is binomiale uitdrukkings van twee terme wat deur `n plus- of minusteken verbind word, soos 
Trappe
Deel 1 van 3: Faktorering van binomiale

1. Hersien weer die basiese beginsels van faktorisering. Faktorering is om `n groot getal in sy eenvoudigste delers te verdeel. Elkeen van hierdie dele word `n `faktor` genoem. Byvoorbeeld, die getal 6 is deelbaar deur vier verskillende getalle: 1, 2, 3 en 6. So 1, 2, 3 en 6 is die faktore van 6.
- Die faktore van 32 is 1, 2, 4, 8, 16 en 32
- Beide `1` en die getal wat jy faktor is altyd faktore. Die faktore van `n klein getal soos 3 is dus net 1 en 3.
- Faktore is slegs daardie getalle wat volledig deelbaar is, dit wil sê die `hele` getalle. Jy kan 32 deur 3,564 of 21,4952 deel, maar dit is nie faktore nie, net desimale getalle.

2. Lys die terme van die binomiaal om dit makliker te maak om te lees. `n Binomiaal is niks anders as die optel of aftrekking van twee terme, waarvan ten minste een `n veranderlike bevat nie. Soms het hierdie veranderlikes eksponente, soos  of
of  . As jy vir die eerste keer probeer om binomiale te faktoriseer, help dit om die vergelykings in dalende veranderlike terme te orden, wat beteken dat die grootste eksponent laaste kom. Byvoorbeeld:
. As jy vir die eerste keer probeer om binomiale te faktoriseer, help dit om die vergelykings in dalende veranderlike terme te orden, wat beteken dat die grootste eksponent laaste kom. Byvoorbeeld:
 of
of  . As jy vir die eerste keer probeer om binomiale te faktoriseer, help dit om die vergelykings in dalende veranderlike terme te orden, wat beteken dat die grootste eksponent laaste kom. Byvoorbeeld:
. As jy vir die eerste keer probeer om binomiale te faktoriseer, help dit om die vergelykings in dalende veranderlike terme te orden, wat beteken dat die grootste eksponent laaste kom. Byvoorbeeld: →
→ 
 →
→ 
 →
→ 

3. Vind die grootste gemene deler van beide terme. Dit beteken dat jy op soek is na die grootste getal waarmee beide dele van die binomiaal deelbaar is. As dit nie werk nie, faktoreer beide getalle op hul eie en kyk wat die hoogste ooreenstemmende getal is. Byvoorbeeld:
 .
.
4. Verdeel die grootste gemene deler vir elke term. As jy die gemene deler ken, moet jy dit uit elke term verwyder. Let daarop dat jy net die terme verdeel wat elkeen `n kleiner delingsprobleem maak. As dit korrek gedoen word, het beide vergelykings dieselfde faktor:
 .
.

5. Vermenigvuldig jou faktor met die resulterende uitdrukking om af te rond. In die laaste probleem het jy `n 3 verwyder en jy kry  . Maar jy wil nie heeltemal van die 3 ontslae raak nie, neem dit net in om dinge te vereenvoudig. Jy kan nie net nommers uitvee sonder om dit terug te plaas nie! Vermenigvuldig die faktor met die uitdrukking om hierdie afdeling te voltooi. Byvoorbeeld:
. Maar jy wil nie heeltemal van die 3 ontslae raak nie, neem dit net in om dinge te vereenvoudig. Jy kan nie net nommers uitvee sonder om dit terug te plaas nie! Vermenigvuldig die faktor met die uitdrukking om hierdie afdeling te voltooi. Byvoorbeeld:
 . Maar jy wil nie heeltemal van die 3 ontslae raak nie, neem dit net in om dinge te vereenvoudig. Jy kan nie net nommers uitvee sonder om dit terug te plaas nie! Vermenigvuldig die faktor met die uitdrukking om hierdie afdeling te voltooi. Byvoorbeeld:
. Maar jy wil nie heeltemal van die 3 ontslae raak nie, neem dit net in om dinge te vereenvoudig. Jy kan nie net nommers uitvee sonder om dit terug te plaas nie! Vermenigvuldig die faktor met die uitdrukking om hierdie afdeling te voltooi. Byvoorbeeld:




6. Kontroleer jou werk deur na die oorspronklike vergelyking te vermenigvuldig. As jy alles reg gedoen het, is dit maklik om te kyk of jy dit reg gedoen het. Vermenigvuldig jou faktor met beide individuele terme tussen hakies. As dit ooreenstem met die oorspronklike gegewe binomiaal, dan het jy dit reg gedoen. Van begin tot einde los ons die uitdrukking op  om te oefen:
om te oefen:
 om te oefen:
om te oefen:




Deel 2 van 3: Faktorering van binomiale om vergelykings op te los

1. Faktor om vergelykings te vereenvoudig sodat dit makliker is om op te los. Wanneer `n vergelyking met binomiale opgelos word, veral komplekse binomiale, kan dit lyk asof daar geen manier is om alles te laat ooreenstem nie. Probeer byvoorbeeld om die volgende op te los:  . Een manier om dit te doen, veral met eksponente, is om eers te faktoriseer.
. Een manier om dit te doen, veral met eksponente, is om eers te faktoriseer.
 . Een manier om dit te doen, veral met eksponente, is om eers te faktoriseer.
. Een manier om dit te doen, veral met eksponente, is om eers te faktoriseer. - Oefenopdrag:
- Onthou dat binomiale slegs twee terme kan hê. As daar meer as twee terme is, moet jy leer om polinome op te los.

2. Tel en trek af sodat een kant van die vergelyking gelyk is aan nul. Hierdie hele strategie maak staat op een van die mees fundamentele feite van wiskunde: iets vermenigvuldig met nul moet gelyk wees aan nul. So as jou vergelyking gelyk is aan nul, dan moet een van die gefaktoriseerde terme gelyk aan nul wees! Om te begin, sal jy optel en aftrek sodat een kant gelyk is aan nul.




3. Los die nie-nul kant op soos jy gewoond is. Op hierdie stadium maak jy net asof die ander kant nie bestaan nie. Vind die grootste gemene deler, verdeel dit en skep dan jou gefaktoriseerde uitdrukking.




4. Stel die terme binne en buite die hakies gelyk aan nul. In die oefenprobleem vermenigvuldig jy 2y met (4 – y), en dit moet gelyk wees aan nul. Aangesien iets vermenigvuldig met nul gelyk is aan nul, beteken dit dat 2y of (4 – y) nul moet wees. Maak twee afsonderlike vergelykings om uit te vind watter waarde y moet hê om weerskante gelyk aan nul te maak.






5. Los beide vergelykings vir nul op vir die finale antwoord of antwoorde. Jy kan een antwoord of veelvuldige antwoorde kry. Onthou, net een kant moet gelyk wees aan nul, sodat jy `n paar verskillende waardes vir y kan kry wat dieselfde vergelyking oplos. Die laaste stappe van die oefenopdrag:





6. Pas jou antwoorde terug op die oorspronklike vergelyking om seker te maak hulle is korrek. Sodra jy die regte waardes vir y gevind het, behoort jy dit te kan gebruik om die vergelyking op te los. Dit is so eenvoudig soos om elke waarde van y uit te probeer in plaas van die veranderlike soos hieronder getoon. Die antwoorde is y = 0 en y = 4, dus:


 Hierdie antwoord is korrek
Hierdie antwoord is korrek

 Hierdie antwoord is ook korrek.
Hierdie antwoord is ook korrek.Deel 3 van 3: Hanteer moeiliker probleme

1. Onthou dat veranderlikes as faktore tel, selfs met eksponente. Onthou dat faktorisering gaan oor die bepaling van watter getalle in die heelgetal pas. Die uitdrukking  is `n ander manier om te sê
is `n ander manier om te sê  . Dit beteken dat jy enige x buite hakies kan plaas as die ander term ook een het. Behandel veranderlikes soos gereelde getalle. Byvoorbeeld:
. Dit beteken dat jy enige x buite hakies kan plaas as die ander term ook een het. Behandel veranderlikes soos gereelde getalle. Byvoorbeeld:
 is `n ander manier om te sê
is `n ander manier om te sê  . Dit beteken dat jy enige x buite hakies kan plaas as die ander term ook een het. Behandel veranderlikes soos gereelde getalle. Byvoorbeeld:
. Dit beteken dat jy enige x buite hakies kan plaas as die ander term ook een het. Behandel veranderlikes soos gereelde getalle. Byvoorbeeld: kan in berekening gebring word, want beide terme bevat `n t. Die finale antwoord sal wees
- Jy kan selfs verskeie veranderlikes buite hakies op dieselfde tyd plaas. Byvoorbeeld, in
beide terme bevat dieselfde
. Jy kan dit oplos in

2. Herken nog nie vereenvoudigde binomiale deur soortgelyke terme te kombineer. Neem byvoorbeeld die uitdrukking  . Hier wil dit voorkom asof jy met vier terme te doen het, maar as jy van nader kyk sal jy agterkom dat daar net twee is. Jy kan soortgelyke terme byvoeg en aangesien beide 6 en 14 geen veranderlike het nie en 2x en 3x dieselfde veranderlike deel, kan hulle saamgevoeg word. Oplos is dan maklik:
. Hier wil dit voorkom asof jy met vier terme te doen het, maar as jy van nader kyk sal jy agterkom dat daar net twee is. Jy kan soortgelyke terme byvoeg en aangesien beide 6 en 14 geen veranderlike het nie en 2x en 3x dieselfde veranderlike deel, kan hulle saamgevoeg word. Oplos is dan maklik:
 . Hier wil dit voorkom asof jy met vier terme te doen het, maar as jy van nader kyk sal jy agterkom dat daar net twee is. Jy kan soortgelyke terme byvoeg en aangesien beide 6 en 14 geen veranderlike het nie en 2x en 3x dieselfde veranderlike deel, kan hulle saamgevoeg word. Oplos is dan maklik:
. Hier wil dit voorkom asof jy met vier terme te doen het, maar as jy van nader kyk sal jy agterkom dat daar net twee is. Jy kan soortgelyke terme byvoeg en aangesien beide 6 en 14 geen veranderlike het nie en 2x en 3x dieselfde veranderlike deel, kan hulle saamgevoeg word. Oplos is dan maklik:





3. Herken die spesiale `verskil van perfekte vierkante`. `n Volmaakte vierkant is `n getal waarvan die wortel `n heelgetal is, soos 
 ,
, 
 , of selfs
, of selfs 
 As jou binomiaal `n minussom is met twee perfekte vierkante, soos
As jou binomiaal `n minussom is met twee perfekte vierkante, soos  , dan kan jy hulle net in hierdie formule gebruik:
, dan kan jy hulle net in hierdie formule gebruik:

 ,
, 
 , of selfs
, of selfs 
 As jou binomiaal `n minussom is met twee perfekte vierkante, soos
As jou binomiaal `n minussom is met twee perfekte vierkante, soos  , dan kan jy hulle net in hierdie formule gebruik:
, dan kan jy hulle net in hierdie formule gebruik:





4. Leer om die `verskil van perfekte kubusse` te vereenvoudig. Soos die perfekte vierkante, is dit `n eenvoudige formule waar twee kubusse van mekaar afgetrek word. Byvoorbeeld,  . Soos voorheen, vind die derdemagswortel van elkeen en gebruik dit in die formule:
. Soos voorheen, vind die derdemagswortel van elkeen en gebruik dit in die formule:
 . Soos voorheen, vind die derdemagswortel van elkeen en gebruik dit in die formule:
. Soos voorheen, vind die derdemagswortel van elkeen en gebruik dit in die formule:

![Faktorering van binomiale {sqrt[ {3}]{8x^{3}}}=2x](https://wikimedia.org/api/rest_v1/media/math/render/svg/77ed49f7f0ab2dfb9de3438ac123641fb683a0a0)
![Faktorering van binomiale {sqrt[ {3}]{27}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca5392df17ff31f62e3cae649d51dd36bde856ce)


5. Weet dat die som van perfekte kubusse ook in `n formule pas. Anders as die verskil van perfekte vierkante, kan jy bygevoegde blokkies gebruik, soos  , ook maklik om te vind met `n eenvoudige formule. Dit is amper presies dieselfde as hierbo, maar met `n paar plus- en minusse omgekeer. Die formule is net so maklik soos die ander twee, en al wat jy hoef te doen is om die twee blokkies in die probleem te herken:
, ook maklik om te vind met `n eenvoudige formule. Dit is amper presies dieselfde as hierbo, maar met `n paar plus- en minusse omgekeer. Die formule is net so maklik soos die ander twee, en al wat jy hoef te doen is om die twee blokkies in die probleem te herken:
 , ook maklik om te vind met `n eenvoudige formule. Dit is amper presies dieselfde as hierbo, maar met `n paar plus- en minusse omgekeer. Die formule is net so maklik soos die ander twee, en al wat jy hoef te doen is om die twee blokkies in die probleem te herken:
, ook maklik om te vind met `n eenvoudige formule. Dit is amper presies dieselfde as hierbo, maar met `n paar plus- en minusse omgekeer. Die formule is net so maklik soos die ander twee, en al wat jy hoef te doen is om die twee blokkies in die probleem te herken:

![Faktorering van binomiale {sqrt[ {3}]{8x^{3}}}=2x](https://wikimedia.org/api/rest_v1/media/math/render/svg/77ed49f7f0ab2dfb9de3438ac123641fb683a0a0)
![Faktorering van binomiale {sqrt[ {3}]{27}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca5392df17ff31f62e3cae649d51dd36bde856ce)

Wenke
- Nie alle binomiale het gemeenskaplike delers nie! Sommige is reeds soveel as moontlik vereenvoudig.
- As jy nie seker is of daar `n gemeenskaplike deler is nie, deel eers deur kleiner getalle. Byvoorbeeld, as jy nie dadelik sien dat 16 die gemene deler van 32 en 16 is nie, begin beide getalle deur 2 deel. Dit laat 16 en 8 oor, wat ook deur 8 gedeel kan word. Nou het jy 2 en 1, die kleinste faktore. Daar is duidelik `n gemene deler groter as 8 en 2.
- Let daarop dat `n sesde mag (x) albei `n perfekte vierkant is en is `n perfekte kubus. So jy kan enige spesiale formule hierbo toepas, in enige volgorde, op `n binomiaal wat die verskil is van perfekte sesde magte, soos x - 64. Jy sal dit egter makliker vind om eers die verskilformule vir perfekte vierkante toe te pas sodat jy die binomiaal verder kan faktoriseer.
Waarskuwings
- `n Binomiaal wat die som van perfekte vierkante is, kan nie in berekening gebring word nie.
Artikels oor die onderwerp "Faktorering van binomiale"
Оцените, пожалуйста статью
Soortgelyk
Gewilde