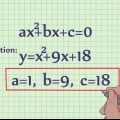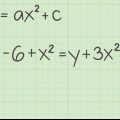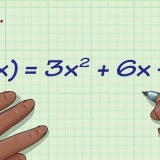In die voorbeeldvergelyking hierbo, as jy albei kante deel deur 2, 2x = 6, kry jy 2/2 x = 6/2, of x = 3. Dit is die x-afsnit vir die vergelyking 2x + 3y = 6. Jy kan dieselfde stappe gebruik vir vergelykings van die vorm ax^2 + by^2 = c. In hierdie geval, as jy 0 vir y invoer, kry jy x^2 = c/a, en nadat jy die waarde regs van die gelykheidsteken gevind het, moet jy die wortel van x-kwadraat vind. Dit gee jou 2 waardes, 1 positief en 1 negatief, wat optel tot 0. 

Faktorering is die verdeling van `n kwadratiese vergelyking in 2 eenvoudiger algebraïese uitdrukkings wat, wanneer saam vermenigvuldig, die kwadratiese vergelyking produseer. Dikwels kan die waardes van a en c die sleutel wees om die korrekte faktore te vind. Aangesien 2 maal 5 gelyk is aan 10, is die absolute waarde van c, en omdat die absolute waarde van b minder as dié van c is, is 2 en 5 waarskynlik die numeriese komponente van die korrekte faktore. Aangesien 5 minus 2 gelyk is aan 3, is die korrekte faktore x + 5 en x - 2. As jy die faktore vir die kwadratiese vergelyking invul, (x + 5)(x - 2) = 0, is die 2x-kruisings -5 (-5 + 5 = 0) en 2 (2 - 2 = 0). As jy die kwadratiese formule gebruik, voeg die waardes vir a, b en c van die kwadratiese formule in die formule (-b + of - W (b^2 - 4 ac))/2a (waar W die vierkant is) in root ) om die waarde of waardes vir x te vind. As jy die waardes 1, 3 en -10 in hierdie vergelyking inprop, kry jy (-3 + of - W (3^2 - 4(1)(-10)))/2(1). Die waarde binne die W-hakies kom uit na 9 -(-40) of 9+40, wat 49 is, so die vergelyking kom uit na (-3 + of - 7)/2, wat lei tot (-3 + 7 ) /2 of 4/2, wat 2 is, en (-3 -7)/2 of -10/2, wat -5 is. Anders as die eenvoudige 2-veranderlike vergelykings wat in die vorige afdeling beskryf is, word kwadratiese vergelykings op `n koördinaatgrafiek as `n parabool geteken (`n geboë lyn wat lyk soos `n "JY" of "V") in plaas van `n reguit lyn. Kwadratiese vergelykings kan geen x-kruising, 1 x kruising of 2 x snyding hê nie.
Vind die kruising met die x-as
Inhoud
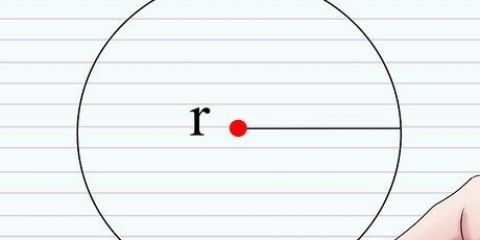
In algebra het 2-dimensionele grafieke met koördinate `n horisontale as, of x-as, en `n vertikale as, of y-as. Die plekke waar lyne wat `n reeks waardes verteenwoordig hierdie asse sny, word kruisings genoem. Die y-afsnit is waar die lyn die y-as sny, en die x-afsnit is waar die lyn die x-as sny. Om die x-afsnit met algebra te vind kan eenvoudig of ingewikkeld wees, afhangende van of die vergelyking slegs 2 veranderlikes het, of kwadraties is. Die stappe hieronder wys hoe dit werk vir beide tipes vergelykings.
Trappe
Metode 1 van 2: Eenvoudige vergelykings met 2 veranderlikes

1. Vervang die waarde van y met 0. By die punt waar die lyn van waardes die horisontale as kruis, het y `n waarde van 0.
- In die voorbeeldvergelyking, as jy 2x + 3y = 6, y met 0 vervang, verander die vergelyking na 2x + 3(0) = 6, dus basies net 2x = 6.

2. Vind die oplossing vir x. Dit beteken gewoonlik om beide kante van die vergelyking te deel deur die koëffisiënt vir x om dit `n waarde van 1 te gee.
Metode 2 van 2: Vir kwadratiese vergelykings

1. Plaas die vergelyking in die vorm ax^2 + bx + c = 0. Dit is die standaardvorm vir die skryf van `n kwadratiese vergelyking, waar a die koëffisiënt vir x-kwadraat is, b die koëffisiënt vir x is, en c `n suiwer numeriese waarde is.
- Vir die voorbeeld in hierdie afdeling, sal ons die vergelyking x^2 +3x - 10 = 0 gebruik.

2. Los die vergelyking vir x op. Daar is verskeie maniere om `n kwadratiese vergelyking op te los. Die 2 waarmee ons hier te doen het, is faktorisering en gebruik die kwadratiese formule.
Wenke
- As in die voorbeeld vergelyking hieronder "Eenvoudige vergelykings met 2 veranderlikes" deur `n 0 vir x in plaas van y in te voer, kan jy die waarde van die y-afsnit uitvind.
Artikels oor die onderwerp "Vind die kruising met die x-as"
Оцените, пожалуйста статью
Gewilde