Vind die domein van 'n funksie

Inhoud

Trappe

Die domein van `n funksie is `n versameling getalle wat binne daardie funksie pas. Met ander woorde, dit is `n versameling x-waardes wat met `n gegewe vergelyking geassosieer word. Die stel y-waardes word genoem reeks funksie. As jy wil weet hoe om die domein van `n funksie in verskillende situasies te vind, volg hierdie stappe.

Trappe

Metode 1 van 6: Leer die basiese beginsels

Prent getiteld Vind die domein van `n funksie Stap 1

1. Leer die definisie van `n domein. `n Domein van `n funksie word gedefinieer as die versameling van alle reële getalle wat as insette vir daardie funksie kan dien. Met ander woorde, `n domein is die volledige stel x-waardes wat in `n funksie ingevoer word, wat lei tot `n stel y-waardes.

Prent getiteld Vind die domein van `n funksie Stap 2

2. Leer hoe om die domein van verskillende funksies te vind. Die tipe kenmerk sal die beste metode bepaal om `n domein te vind. Hier is die basiese beginsels wat jy nodig het vir die volgende funksies:

`n Polinoom sonder wortels of breuke met veranderlikes in die noemer. Die domein van hierdie tipe funksie bestaan uit die versameling van alle reële getalle.

`n Funksie met `n breuk met `n veranderlike in die noemer. Om die domein van hierdie tipe funksie te vind, stel die noemer van die breuk gelyk aan nul en ignoreer die x-waarde wat jy kry nadat jy die vergelyking opgelos het.

`n Funksie met `n veranderlike binne `n radikaal. Om die domein van hierdie tipe funksie te vind, stel die terme binne die radikaal groter as 0 en los die vergelyking op om uit te vind watter waardes vir x korrek is binne hierdie funksie.

`n Funksie met `n natuurlike logaritme (ln). Maak die terme tussen hakies >0 en los op.

`n Grafiek. Lei uit die grafiek af watter waardes korrek is vir x.

N verhouding. Dit is `n lys van x- en y-koördinate. Jou domein is bloot `n lys van x-koördinate.

Prent getiteld Vind die domein van `n funksie Stap 3

3. Verstaan die notasie van `n domein. Die korrekte notasie van `n domein is maklik om te leer, maar dit is belangrik dat jy dit korrek doen om nie punte in toetse en eksamens te mis nie. Hier is `n paar dinge wat jy moet weet om die domein van `n funksie korrek te skryf:

Die struktuur van `n domein is `n oop vierkantige/ronde hakie, gevolg deur die 2 eindpunte van die domein geskei deur `n komma en gevolg deur `n sluitende vierkantige/ronde hakie.

Byvoorbeeld: [-1.5). Dit beteken dat die domein van -1 na 5 gaan.

Gebruik vierkantige hakies soos [ en ] om aan te dui of `n getal binne `n sekere domein val.

Dus in die voorbeeld, [-1.5), val -1 binne die domein.

Gebruik hakies soos ( en ) om aan te dui dat `n getal buite `n sekere domein is.

So in die voorbeeld, [-1.5), is die 5 buite die domein. Die domein stop op enige punt voor die 5, byvoorbeeld 4 999 ..

Gebruik "U" (betekenis "vakbond") om dele van die domein wat van mekaar geskei is, te verbind.`

Byvoorbeeld: [-1.5) U (5.10]. Dit beteken dat die domein van -1 na 10 gaan, maar daar is `n gaping in die domein by 5. Dit kan byvoorbeeld wees as gevolg van `n funksie met "x - 5" in die noemer.

jy kan soveel doen "JY"-gebruik simbole soos nodig, as die domein veelvuldige breuke het.

Gebruik die oneindigheidsimbool (in positiewe en negatiewe rigtings) om aan te dui dat in daardie rigting die domein oneindig is.

By oneindig, gebruik altyd ( ) en nie [ ].

Metode 2 van 6: Vind die domein van `n funksie wat `n breuk bevat

Prent getiteld Vind die domein van `n funksie Stap 4

1. Skryf die opdrag. Gestel jy het die volgende probleem:

f(x) = 2x/(x - 4)

Prent getiteld Vind die domein van `n funksie Stap 5

2. Vir breuke met `n veranderlike in die noemer, stel jy hierdie veranderlike gelyk aan nul in `n vergelyking. As jy die domein van `n funksie met `n breuk wil vind, sluit alle x-waardes uit wat die noemer gelyk aan nul maak, want jy kan nooit deur nul deel nie. Skryf dus die noemer as `n vergelyking en stel dit gelyk aan 0. Hier is hoe om dit te doen:

f(x) = 2x/(x - 4)

x - 4 = 0

(x - 2 )(x + 2) = 0

x ≠ (2, - 2)

Prent getiteld Vind die domein van `n funksie Stap 6

3. Maak `n nota van die domein. Hier is hoe om dit te doen:

x = alle reële getalle behalwe 2 en -2

Metode 3 van 6: Vind die domein van `n funksie met `n vierkantswortel

Prent getiteld Vind die domein van `n funksie Stap 7

1. Skryf die opdrag. Gestel jy het die volgende probleem: Y = (x-7)

Prent getiteld Vind die domein van `n funksie Stap 8

2. Maak seker dat die terme binne die vierkantswortel groter as of gelyk aan 0 kan wees. Jy kan nie die vierkantswortel van `n negatiewe getal neem nie, maar jy kan die vierkantswortel van nul neem. Let daarop dat dit nie net van toepassing is op vierkantswortels nie, maar vir alle ewe wortelgetalle. Dit is nie van toepassing op onewe radikale getalle nie, want dit is nie `n probleem as daar `n negatiewe getal onder die radikale teken is nie. Hier is `n voorbeeld:

x-7 0

Prent getiteld Vind die domein van `n funksie Stap 9

3. Isoleer die veranderlike. Om nou x aan die linkerkant van die vergelyking te skei, tel 7 by albei kante van die gelyktekens by, sodat dit na hierdie bewerking so sal lyk:

x 7

Prent getiteld Vind die domein van `n funksie Stap 10

4. Skryf die domein korrek. Dit is die korrekte notasie:

D = [7,∞)

Prent getiteld Vind die domein van `n funksie Stap 11

5. Vind die domein van `n funksie met `n vierkantswortel as veelvuldige oplossings moontlik is. Gestel jy het die volgende funksie: y = 1/√( ̅x -4). As jy die noemer buite die hakies neem en dit gelyk aan nul maak, kry jy x ≠ (2, - 2). Hier is hoe om voort te gaan:

Kontroleer nou die area onder -2 (deur bv. -3), of dit `n resultaat groter as nul gee. Dit is reg.

(-3) - 4 = 5

Kontroleer nou die area tussen -2 en 2. Neem byvoorbeeld 0.

0 - 4 = -4, so jy weet die getalle tussen -2 en 2 werk nie.

Probeer nou `n getal bo 2, soos +3.

3 - 4 = 5, dus die getalle bo 2 werk.

Skryf die domein neer wanneer jy klaar is. Hier is hoe om dit neer te skryf:

D = (-∞, -2) U (2, ∞)

Metode 4 van 6: Vind die domein van `n funksie deur die natuurlike logaritme te gebruik

Prent getiteld Vind die domein van `n funksie Stap 12

1. Skryf die opdrag. Gestel jy het hierdie:

f(x) = ln(x-8)

Prent getiteld Vind die domein van `n funksie Stap 13

2. Maak die terme binne die hakies groter as nul. Die natuurlike logaritme moet positief wees, dus maak die terme binne die hakies groter as nul. Hier is `n voorbeeld:

x - 8 > 0

Prent getiteld Vind die domein van `n funksie Stap 14

3. Los op. Skei die veranderlike x deur 8 aan beide kante van die vergelyking by te tel. Hier is hoe:

x - 8 + 8 > 0 + 8

X > 8

Prent getiteld Vind die domein van `n funksie Stap 15

4. Maak `n nota van die domein. Toon aan dat die domein van hierdie vergelyking gelyk is aan alle getalle groter as 8 tot oneindig. Hier is hoe:

D = (8,∞)

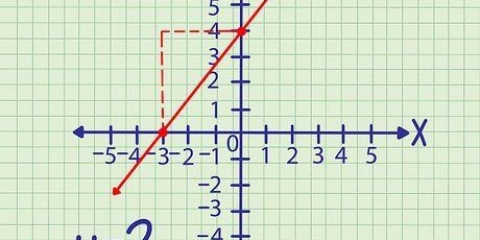
Metode 5 van 6: Vind die domein van `n funksie deur `n grafiek te gebruik

Prent getiteld Vind die domein van `n funksie Stap 16

1. Kyk na die grafiek.

Prent getiteld Vind die domein van `n funksie Stap 17

2. Ondersoek watter x-waardes aan die grafiek behoort. Dit is makliker gesê as gedaan, so hier is `n paar wenke:

`n Lyn. As jy `n lyn op die grafiek na oneindig sien gaan, sal elke x-waarde uiteindelik in die parabool vervat wees, dus is die domein gelyk aan alle reële getalle.

`n Gewone parabool. As jy `n parabool sien wat op of af wys, dan bestaan die domein uit alle reële getalle, want alle getalle op die x-as is uiteindelik in die parabool vervat.

`n Horisontale parabool. As jy te doen het met `n parabool met die hoekpunt by (4,0) wat oneindig na regs strek, dan is jou domein gelyk aan D = [4,∞)

Prent getiteld Vind die domein van `n funksie Stap 18

3. Bepaal die domein. Bepaal die domein gebaseer op die tipe grafiek wat jy het. As jy nie heeltemal seker is nie, maar jy ken die vergelyking van die lyn, voer die x-koördinate in die funksie in om na te gaan.

Metode 6 van 6: Bepaling van die domein van `n funksie deur `n versameling/verwantskap te gebruik

Prent getiteld Vind die domein van `n funksie Stap 19

1. Skryf die verhouding neer. `n Verwantskap is bloot `n reeks x- en y-koördinate. Gestel jy het die volgende koördinate: {(1, 3), (2, 4), (5, 7)}

Prent getiteld Vind die domein van `n funksie Stap 20

2. Skryf die x-koördinate neer. Dit is: 1, 2, 5.

Prent getiteld Vind die domein van `n funksie Stap 21

3. Bepaal die domein. D = {1, 2, 5}

Prent getiteld Vind die domein en omvang van `n funksie Stap 3

4. Maak seker dat hierdie verhouding `n funksie is. `n Verwantskap is `n funksie as elke keer as jy `n numeriese x-koördinaat invoer jy dieselfde y-koördinaat as `n antwoord kry. As jy dus `n 3 voor die x sit, kry jy 6 as die y-waarde, ensovoorts. Die volgende verhouding is nie `n funksie omdat jy twee verskillende y-waardes kry vir elke waarde van "X": {(1, 4),(3, 5),(1, 5)}.