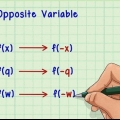
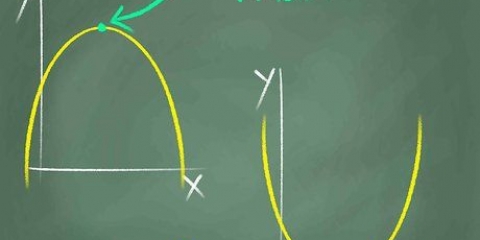
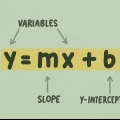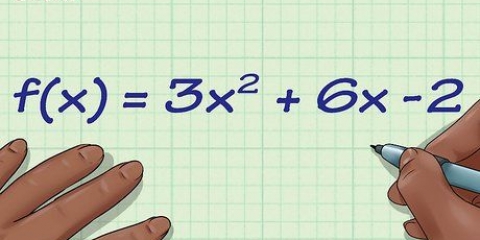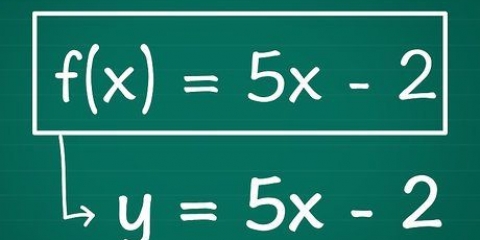As die helling negatief is, beteken dit dat die lyn afgaan wanneer jy na regs gaan. 





-1: -1 + 2 = 1 0: 0 +2 = 2 1: 1 + 2 = 3 




Maak F(x) gelyk aan nul:
Los op:




Sommige kwadratiese funksies, soos  is nooit negatief nie. Daar is dus `n asimptoot by 0.
is nooit negatief nie. Daar is dus `n asimptoot by 0. Tensy jy met denkbeeldige getalle werk, is dit nie moontlik nie: 
Vergelykings met komplekse eksponente kan baie asimptote hê. 
Vir die vergelyking  , kan jy -1, 0, 1, -2, 2, -10 en 10 invul. Dit gee jou `n goeie reeks getalle om te vergelyk.
, kan jy -1, 0, 1, -2, 2, -10 en 10 invul. Dit gee jou `n goeie reeks getalle om te vergelyk. Wees slim om nommers te kies. In die voorbeeld merk jy vinnig op dat `n negatiewe teken nie saak maak nie -- jy kan byvoorbeeld ophou om -10 te toets, want dit sal dieselfde as 10 wees. 
Aanvaar twee tot vier groot waardes vir x, half negatief en half positief, en teken die kolletjies. Wat gebeur as jy `oneindigheid` vir een veranderlike invoeg? Word die funksie oneindig groter of kleiner? As die grade gelyk is in `n breuk, soos  , deel dan net die eerste twee koëffisiënte (
, deel dan net die eerste twee koëffisiënte ( om jou finale asimptoot (-0.5) te kry.
om jou finale asimptoot (-0.5) te kry. As die grade in `n breuk verskil, deel die vergelyking in die teller deur die vergelyking in die noemer deur polinoom-langdeling te gebruik. 

Teken die grafiek van 'n funksie
Inhoud
`n Grafiek van `n funksie is `n visuele voorstelling van die gedrag van `n funksie op `n x-y-vlak. Grafieke help ons om verskeie aspekte van die funksie te verstaan wat moeilik sal wees om te verstaan deur net na die funksie self te kyk. Jy kan duisende vergelykings teken, en daar is verskillende formules vir elke vergelyking. Daar is egter altyd maniere om `n funksie te teken as jy die presiese stappe vir die spesifieke tipe funksie vergeet het.
Trappe
Metode 1 van 3: Teken `n lineêre vergelyking met `n raaklyn

1. Weet dat lineêre funksies eenvoudige lyne is wat maklik is om te teken, soos bv y = 2 X + 5  . Daar is een veranderlike en een konstante, geskryf as
. Daar is een veranderlike en een konstante, geskryf as  in `n lineêre funksie, sonder eksponente, radikale, ens. As jy so `n eenvoudige vergelyking het, is die grafiek van die funksie ook eenvoudig. Ander voorbeelde van lineêre funksies is:
in `n lineêre funksie, sonder eksponente, radikale, ens. As jy so `n eenvoudige vergelyking het, is die grafiek van die funksie ook eenvoudig. Ander voorbeelde van lineêre funksies is:
 . Daar is een veranderlike en een konstante, geskryf as
. Daar is een veranderlike en een konstante, geskryf as  in `n lineêre funksie, sonder eksponente, radikale, ens. As jy so `n eenvoudige vergelyking het, is die grafiek van die funksie ook eenvoudig. Ander voorbeelde van lineêre funksies is:
in `n lineêre funksie, sonder eksponente, radikale, ens. As jy so `n eenvoudige vergelyking het, is die grafiek van die funksie ook eenvoudig. Ander voorbeelde van lineêre funksies is: 
2. Gebruik die konstante om die snypunt met die y-as aan te dui. Die snypunt met die y-as is die punt waar die funksie die y-as op jou grafiek kruis. Met ander woorde, dit is die punt waar  . So om dit te vind, stel net x op nul en laat die konstante in die vergelyking. In die vorige voorbeeld,
. So om dit te vind, stel net x op nul en laat die konstante in die vergelyking. In die vorige voorbeeld,  , is die snypunt met die y-as gelyk aan y=5, dit wil sê die punt (0.5). Merk hierdie plek op jou grafiek met `n punt.
, is die snypunt met die y-as gelyk aan y=5, dit wil sê die punt (0.5). Merk hierdie plek op jou grafiek met `n punt.
 . So om dit te vind, stel net x op nul en laat die konstante in die vergelyking. In die vorige voorbeeld,
. So om dit te vind, stel net x op nul en laat die konstante in die vergelyking. In die vorige voorbeeld,  , is die snypunt met die y-as gelyk aan y=5, dit wil sê die punt (0.5). Merk hierdie plek op jou grafiek met `n punt.
, is die snypunt met die y-as gelyk aan y=5, dit wil sê die punt (0.5). Merk hierdie plek op jou grafiek met `n punt.
3. Vind die helling van jou lyn met die getal net voor die veranderlike. In die voorbeeld,  , is die helling `2`. Dit is omdat 2 aan die veranderlike `x` behoort. Die helling dui aan hoe steil `n lyn is, of hoe hoog die lyn gaan voordat jy regs of links draai. `n Groter helling beteken `n steiler lyn.
, is die helling `2`. Dit is omdat 2 aan die veranderlike `x` behoort. Die helling dui aan hoe steil `n lyn is, of hoe hoog die lyn gaan voordat jy regs of links draai. `n Groter helling beteken `n steiler lyn.
 , is die helling `2`. Dit is omdat 2 aan die veranderlike `x` behoort. Die helling dui aan hoe steil `n lyn is, of hoe hoog die lyn gaan voordat jy regs of links draai. `n Groter helling beteken `n steiler lyn.
, is die helling `2`. Dit is omdat 2 aan die veranderlike `x` behoort. Die helling dui aan hoe steil `n lyn is, of hoe hoog die lyn gaan voordat jy regs of links draai. `n Groter helling beteken `n steiler lyn.
4. Maak `n breukdeel van die helling. Die helling het te doen met die steilte, en steilte is bloot die verskil tussen die beweging op en af, en links en regs. Die helling is `n fraksie van die verandering van y in vergelyking met die verandering van x. Hoeveel moet die reël `oor y verander` voordat dit `oor x verander`? In die voorbeeld kan die helling `2` gelees word as  .
.
 .
.
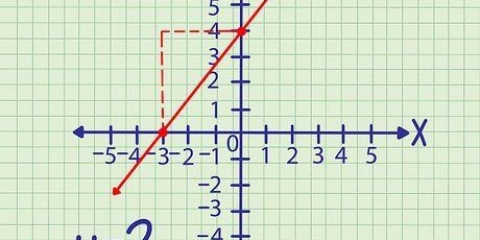
5. Begin by jou kruising met die y-as en volg die veranderinge oor y en x, om meer punte te teken. Sodra jy die helling ken, gebruik dit om jou lineêre funksie te teken. Begin by die kruising met die y-as, hier (0.5), gaan dan op 2, en regs 1. Merk ook hierdie punt (1,7). Soek nog 1-2 punte om die grafiek te teken.

6. Gebruik `n liniaal om jou punte te verbind en teken jou lineêre funksie. Om foute of rowwe grafieke te vermy, vind en verbind ten minste drie afsonderlike punte, hoewel twee in `n noodgeval voldoende sal wees. Dit is die grafiek van jou lineêre vergelyking!
Metode 2 van 3: Skat punte op `n grafiek

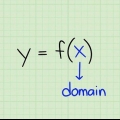
1. Bepaal die funksie. Neem die funksie van die vorm f(X), waar y verteenwoordig die reeks, X verteenwoordig die domein, en f die funksie. As voorbeeld gebruik ons y = x+2, waardeur f(X) = x+2.

2. Trek twee gekruiste lyne op `n vel papier. Die horisontale lyn is jy X-as. Die vertikale lyn is jy y-as.

3. Nommer jou grafiek. Merk beide die X-asof die y-as met getalle ewe ver van mekaar af. Vir die X-as is die getalle positief aan die regterkant en negatief aan die linkerkant. Vir die y-as is die getalle positief aan die bokant en negatief aan die onderkant.

4. Bereken a y-waarde vir 2-3 X-waardes. Aanvaar die funksie f(X) = x+2. Bereken `n paar waardes vir y deur die ooreenstemmende waardes vir X sigbaar op die as in die funksie. Vir meer ingewikkelde vergelykings mag dit nodig wees om die funksie te vereenvoudig deur eers een veranderlike te isoleer.

5. Teken die grafiekpunt vir elke paar. Trek denkbeeldige dun vertikale lyne langs die X-as en horisontaal langs die y-as. Die punt waar hierdie lyne sny, is `n grafiekpunt (of gebruik net grafiekpapier).

6. Verwyder die denkbeeldige lyne. Wanneer jy al die grafiekpunte geteken het, kan jy die denkbeeldige lyne uitvee. Let wel: die grafiek van f(x) = x sal `n lyn parallel daarmee wees deur die oorsprong (0,0), maar f(x) = x+2 word twee eenhede (langs die y-as) op die rooster geskuif as gevolg van die +2 in die vergelyking.
Metode 3 van 3: Teken `n komplekse funksie

1. Verstaan hoe om algemene tipes vergelykings grafies voor te stel. Daar is soveel verskillende kaartstrategieë as wat daar tipes funksies is, heeltemal te veel om hier volledig te dek. As jy dit moeilik vind en `n skatting werk nie, kyk na artikels oor:
- Kwadratiese funksies
- Rasionele Funksies
- Logaritmiese funksies
- Ongelykhede (geen kenmerke, maar nuttige inligting nietemin).

2.Bepaal eers die nulle. Nulle is die punte waar die grafiek die horisontale lyn op die grafiek sny. Alhoewel nie alle grafieke nulle het nie, het die meeste dit, en dit is die eerste stap wat jy moet neem om alles reg te kry. Om nulle te vind, stel eers die hele funksie op nul, en los dit dan op. Byvoorbeeld:







3. Vind en merk enige horisontale asimptote (plekke waar die funksie onmoontlik is om te bereik) met `n stippellyn. Dit is gewoonlik punte waar die grafiek nie bestaan nie, soos waar jy deur nul deel. As jou vergelyking `n veranderlike in `n breuk het, soos  , begin dan deur die onderkant van die breuk te nul. Jy kan alle plekke uitbeeld waar dit gelyk is aan nul (in hierdie voorbeeld `n stippellyn by x=2 en x=-2), want jy kan nooit deur nul deel nie. Breuke is egter nie die enigste plekke om asimptote te vind nie. Gewoonlik is al wat jy nodig het `n bietjie gesonde verstand:
, begin dan deur die onderkant van die breuk te nul. Jy kan alle plekke uitbeeld waar dit gelyk is aan nul (in hierdie voorbeeld `n stippellyn by x=2 en x=-2), want jy kan nooit deur nul deel nie. Breuke is egter nie die enigste plekke om asimptote te vind nie. Gewoonlik is al wat jy nodig het `n bietjie gesonde verstand:
 , begin dan deur die onderkant van die breuk te nul. Jy kan alle plekke uitbeeld waar dit gelyk is aan nul (in hierdie voorbeeld `n stippellyn by x=2 en x=-2), want jy kan nooit deur nul deel nie. Breuke is egter nie die enigste plekke om asimptote te vind nie. Gewoonlik is al wat jy nodig het `n bietjie gesonde verstand:
, begin dan deur die onderkant van die breuk te nul. Jy kan alle plekke uitbeeld waar dit gelyk is aan nul (in hierdie voorbeeld `n stippellyn by x=2 en x=-2), want jy kan nooit deur nul deel nie. Breuke is egter nie die enigste plekke om asimptote te vind nie. Gewoonlik is al wat jy nodig het `n bietjie gesonde verstand: is nooit negatief nie. Daar is dus `n asimptoot by 0.
is nooit negatief nie. Daar is dus `n asimptoot by 0.

4. Pas die waardes toe en teken verskillende punte. Kies net `n paar waardes vir x en los vir die funksie op. Maak dan `n grafiek van die punte op jou grafiek. Hoe ingewikkelder die grafiek, hoe meer punte benodig jy. Oor die algemeen is -1, 0 en 1 die maklikste punte om te kry, alhoewel jy nog twee of drie aan weerskante van die nul wil hê om `n goeie grafiek te kry.
 , kan jy -1, 0, 1, -2, 2, -10 en 10 invul. Dit gee jou `n goeie reeks getalle om te vergelyk.
, kan jy -1, 0, 1, -2, 2, -10 en 10 invul. Dit gee jou `n goeie reeks getalle om te vergelyk.
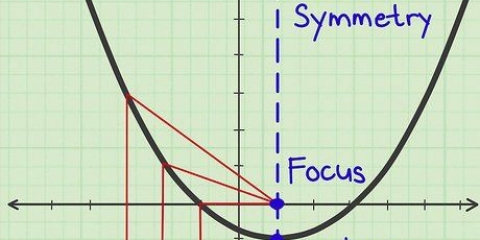
5. Karteer die eindgedrag van die funksie om te sien wat gebeur wanneer dit regtig groot word. Dit gee jou `n idee van die algemene rigting van `n funksie, gewoonlik as `n vertikaal asimptoot. Byvoorbeeld: jy weet dit  word uiteindelik baie, baie groot. Net een ekstra `x` (een miljoen teenoor een miljoen en een) maak y baie groter. Daar is `n paar maniere om die eindgedrag te toets, insluitend:
word uiteindelik baie, baie groot. Net een ekstra `x` (een miljoen teenoor een miljoen en een) maak y baie groter. Daar is `n paar maniere om die eindgedrag te toets, insluitend:
 word uiteindelik baie, baie groot. Net een ekstra `x` (een miljoen teenoor een miljoen en een) maak y baie groter. Daar is `n paar maniere om die eindgedrag te toets, insluitend:
word uiteindelik baie, baie groot. Net een ekstra `x` (een miljoen teenoor een miljoen en een) maak y baie groter. Daar is `n paar maniere om die eindgedrag te toets, insluitend: , deel dan net die eerste twee koëffisiënte (
, deel dan net die eerste twee koëffisiënte ( om jou finale asimptoot (-0.5) te kry.
om jou finale asimptoot (-0.5) te kry.
6. Verbind die kolletjies, vermy asimptotiese en eindgedrag, om die grafiek te skat. Sodra jy vyf of ses punte het, die asimptote en `n algemene idee van die eindgedrag, gebruik al hierdie om `n benaderde weergawe van die grafiek te konstrueer.

7. Gee perfekte grafieke deur `n grafiese sakrekenaar te gebruik. Grafiese sakrekenaars is kragtige handrekenaars wat presiese grafieke vir enige vergelyking kan verskaf. Hulle laat jou toe om presiese punte op te spoor, hellingslyne te vind en moeilike vergelykings met gemak te visualiseer. Voer net die presiese vergelyking in die grafiekafdeling in (gewoonlik `n knoppie gemerk `F(x) = `) en druk die grafiekknoppie om `n idee van die funksie te kry.
Wenke
- Grafiese sakrekenaars is `n goeie manier om te oefen. Probeer om `n grafiek met die hand te maak en gebruik dan die sakrekenaar om `n perfekte prentjie van die grafiek te kry, en vergelyk dan beide grafieke.
- As jy regtig nie meer weet wat om te doen nie, voer net `n paar punte in. Basies kan jy die hele funksie so teken as jy `n oneindige aantal kombinasies van getalle probeer het.
Artikels oor die onderwerp "Teken die grafiek van 'n funksie"
Оцените, пожалуйста статью
Gewilde