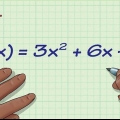word
word 
 word
word 
 word
word  .
.








As die twee resultate dieselfde is, dan is f(x)=f(-x), en die oorspronklike funksie is ewe. `n Voorbeeld is:  en
en  .
.Hierdie twee is dieselfde en dus is die funksie ewe. As elke term van die nuwe weergawe van die funksie die wederkerige van die ooreenstemmende term van die oorspronklike is, dan is f(x)=-f(-x) en die funksie is vreemd. Byvoorbeeld:  maar
maar  .
.Let daarop dat as jy elke term van die eerste funksie met -1 vermenigvuldig, maak jy die tweede funksie. Die oorspronklike funksie g(x) is dus vreemd. As die nuwe funksie nie by een van hierdie twee voorbeelde pas nie, is dit nóg ewe nóg vreemd. Byvoorbeeld:  maar
maar  . Die eerste term is dieselfde in elke funksie, maar die tweede term is `n inverse. Daarom is hierdie funksie nóg ewe nóg vreemd.
. Die eerste term is dieselfde in elke funksie, maar die tweede term is `n inverse. Daarom is hierdie funksie nóg ewe nóg vreemd.

Jy kan vir simmetrie toets deur individuele punte te kies. As die y-waarde van enige x-waarde dieselfde is as die y-waarde van -x, dan is die funksie ewe. Die punte hierbo gekies vir plot  gee die volgende resultate:
gee die volgende resultate: (1.3) en (-1.3) (2.9) en (-2.9). Die ooreenstemmende y-waardes vir x=1 en x=-1, en vir x=2 en x=-2, dui aan dat dit `n ewe funksie is. Vir `n beter toets is die keuse van twee punte nie genoeg bewyse nie, maar dit is `n goeie aanduiding. 
As jy `n paar toetswaardes vir x kies en hul inverse ooreenstemmende waardes vir -x, behoort jy omgekeerde resultate te kry. Oorweeg die kenmerk  . Hierdie funksie gee die volgende punte terug:
. Hierdie funksie gee die volgende punte terug:  . Die punt is (1,2).
. Die punt is (1,2). . Die punt is (-1,-2).
. Die punt is (-1,-2). . Die punt is (2,10).
. Die punt is (2,10). . Die punt is (-2,-10).
. Die punt is (-2,-10).Dus f(x)=-f(-x), en jy kan aflei dat die funksie vreemd is. 
Kies `n paar waardes vir x en -x, soos volg:  . Die punt om te plot is (1,4).
. Die punt om te plot is (1,4). . Die punt om te plot is (-1,-2).
. Die punt om te plot is (-1,-2). . Die punt om te plot is (2,10).
. Die punt om te plot is (2,10). . Die punt om te plot is (2,-2).
. Die punt om te plot is (2,-2).Dit gee jou reeds genoeg punte om op te let dat daar geen simmetrie is nie. Die y-waardes vir teenoorgestelde pare x-waardes is nie dieselfde nie, en ook nie mekaar se inverse nie. Hierdie funksie is nie ewe of vreemd nie. Jy sal dalk hierdie kenmerk sien,  , kan herskryf word as
, kan herskryf word as  . Geskryf in hierdie vorm, lyk dit of dit `n ewe funksie is, want daar is net een eksponent, en dit is `n ewe getal. Hierdie voorbeeld illustreer egter dat jy nie kan bepaal of `n funksie ewe of onewe is wanneer dit tussen hakies ingesluit is nie. Jy moet die funksie in individuele terme evalueer en dan die eksponente ondersoek.
. Geskryf in hierdie vorm, lyk dit of dit `n ewe funksie is, want daar is net een eksponent, en dit is `n ewe getal. Hierdie voorbeeld illustreer egter dat jy nie kan bepaal of `n funksie ewe of onewe is wanneer dit tussen hakies ingesluit is nie. Jy moet die funksie in individuele terme evalueer en dan die eksponente ondersoek.
Weet of 'n funksie ewe of onewe is
Inhoud
Een manier om funksies te klassifiseer is óf `gelyk`, `onewe`, óf nie een nie. Hierdie terme verwys na die herhaling of simmetrie van die funksie. Die beste manier om uit te vind is deur die funksie algebraïes te manipuleer. Jy kan ook die grafiek van die funksie bestudeer en simmetrie soek. Sodra jy weet hoe om kenmerke te klassifiseer, kan jy ook die voorkoms van sekere kombinasies van kenmerke voorspel.
Trappe
Metode 1 van 2: Toets die funksie algebraïes

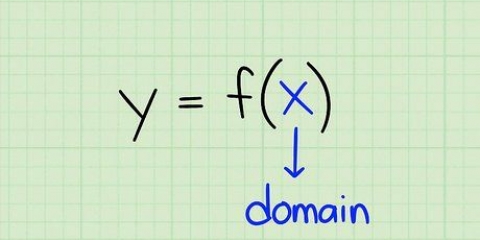
1. Bekyk inverse veranderlikes. In algebra is die wederkerigheid van `n veranderlike negatief. Dit is waar of die veranderlike van die funksie nou  is of iets anders. As die veranderlike van die oorspronklike funksie reeds negatief is (of `n aftrekking), dan is die wederkerige daarvan positief (of `n optelling). Die volgende is `n paar voorbeelde van veranderlikes en hul inverses:
is of iets anders. As die veranderlike van die oorspronklike funksie reeds negatief is (of `n aftrekking), dan is die wederkerige daarvan positief (of `n optelling). Die volgende is `n paar voorbeelde van veranderlikes en hul inverses:
 is of iets anders. As die veranderlike van die oorspronklike funksie reeds negatief is (of `n aftrekking), dan is die wederkerige daarvan positief (of `n optelling). Die volgende is `n paar voorbeelde van veranderlikes en hul inverses:
is of iets anders. As die veranderlike van die oorspronklike funksie reeds negatief is (of `n aftrekking), dan is die wederkerige daarvan positief (of `n optelling). Die volgende is `n paar voorbeelde van veranderlikes en hul inverses: - Die omgekeerde van
is
- Die omgekeerde van
is
- Die omgekeerde van
is
.

2. Vervang elke veranderlike van die funksie met sy inverse. Moenie die oorspronklike funksie verander nie, behalwe die karakter. Byvoorbeeld:
 word
word 
 word
word 
 word
word  .
.
3. Vereenvoudig die nuwe kenmerk. Op hierdie stadium hoef jy nie bekommerd te wees oor die oplossing van die funksie vir `n gegewe numeriese waarde nie. Jy vereenvoudig net die veranderlikes om die nuwe funksie, f(-x), te vergelyk met die oorspronklike funksie, f(x). Onthou die basiese reëls van eksponente wat sê dat `n negatiewe basis tot `n ewe mag positief sal wees, terwyl `n negatiewe basis tot `n onewe mag negatief sal wees.








4. Vergelyk die twee funksies. Vir elke voorbeeld wat jy probeer, vergelyk die vereenvoudigde weergawe van f(-x) met die oorspronklike f(x). Plaas die terme langs mekaar vir maklike vergelyking, en vergelyk die tekens van alle terme.
 en
en  .
. maar
maar  .
. maar
maar  . Die eerste term is dieselfde in elke funksie, maar die tweede term is `n inverse. Daarom is hierdie funksie nóg ewe nóg vreemd.
. Die eerste term is dieselfde in elke funksie, maar die tweede term is `n inverse. Daarom is hierdie funksie nóg ewe nóg vreemd.Metode 2 van 2: Toets die funksie grafies

1. Teken `n grafiek van die funksie. Gebruik grafiekpapier of `n grafiese sakrekenaar om die funksie te teken. Kies verskillende numeriese waardes vir  en prop dit in die funksie om die gevolglike waarde van te kry
en prop dit in die funksie om die gevolglike waarde van te kry  te bereken. Teken hierdie punte op die grafiek en nadat verskeie punte geplot is, trek `n lyn deur hulle om die funksie te teken.
te bereken. Teken hierdie punte op die grafiek en nadat verskeie punte geplot is, trek `n lyn deur hulle om die funksie te teken.
 en prop dit in die funksie om die gevolglike waarde van te kry
en prop dit in die funksie om die gevolglike waarde van te kry  te bereken. Teken hierdie punte op die grafiek en nadat verskeie punte geplot is, trek `n lyn deur hulle om die funksie te teken.
te bereken. Teken hierdie punte op die grafiek en nadat verskeie punte geplot is, trek `n lyn deur hulle om die funksie te teken. - Wanneer u die punte teken, let op positiewe en ooreenstemmende negatiewe waardes vir
. Byvoorbeeld, as jy met die funksie te doen het
, dan plot jy die volgende waardes:
. Dit lei tot die punt
.
. Dit lei tot die punt
.
. Dit lei tot die punt
.
. Dit lei tot die punt
.

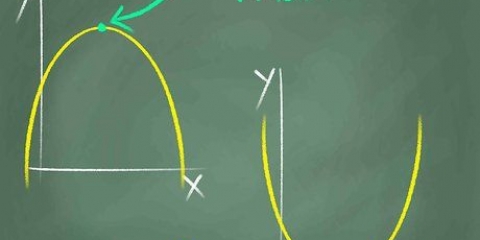
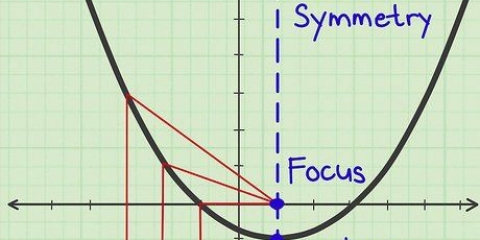
2. Let op simmetrie langs die y-as. Wanneer na `n funksie gekyk word, sal simmetrie `n spieëlbeeld voorstel. As jy sien dat die deel van die grafiek aan die regterkant (positiewe) kant van die y-as ooreenstem met die deel van die grafiek aan die linkerkant (negatiewe) kant van die y-as, dan is die grafiek simmetries om die y-as. As `n funksie simmetries om die y-as is, dan is die funksie ewe.
 gee die volgende resultate:
gee die volgende resultate:
3. Toets vir simmetrie vanaf die oorsprong. Die oorsprong is die sentrale punt (0,0). Oorsprongsimmetrie beteken dat `n positiewe resultaat vir `n gekose x-waarde sal ooreenstem met `n negatiewe resultaat vir -x, en omgekeerd. Vreemde funksies vertoon oorsprongsimmetrie.
 . Hierdie funksie gee die volgende punte terug:
. Hierdie funksie gee die volgende punte terug: . Die punt is (1,2).
. Die punt is (1,2). . Die punt is (-1,-2).
. Die punt is (-1,-2). . Die punt is (2,10).
. Die punt is (2,10). . Die punt is (-2,-10).
. Die punt is (-2,-10).
4. Kyk of daar geen simmetrie is nie. Die laaste voorbeeld is `n funksie met geen simmetrie aan beide kante nie. As jy na die grafiek kyk sal jy sien dat dit nie `n spieëlbeeld op die y-as of om die oorsprong is nie. Bekyk die kenmerk  .
.
 .
. . Die punt om te plot is (1,4).
. Die punt om te plot is (1,4). . Die punt om te plot is (-1,-2).
. Die punt om te plot is (-1,-2). . Die punt om te plot is (2,10).
. Die punt om te plot is (2,10). . Die punt om te plot is (2,-2).
. Die punt om te plot is (2,-2). , kan herskryf word as
, kan herskryf word as  . Geskryf in hierdie vorm, lyk dit of dit `n ewe funksie is, want daar is net een eksponent, en dit is `n ewe getal. Hierdie voorbeeld illustreer egter dat jy nie kan bepaal of `n funksie ewe of onewe is wanneer dit tussen hakies ingesluit is nie. Jy moet die funksie in individuele terme evalueer en dan die eksponente ondersoek.
. Geskryf in hierdie vorm, lyk dit of dit `n ewe funksie is, want daar is net een eksponent, en dit is `n ewe getal. Hierdie voorbeeld illustreer egter dat jy nie kan bepaal of `n funksie ewe of onewe is wanneer dit tussen hakies ingesluit is nie. Jy moet die funksie in individuele terme evalueer en dan die eksponente ondersoek.Wenke
- As alle vorme van `n veranderlike in die funksie ewe eksponente het, dan is die funksie ewe. As alle eksponente vreemd is, dan is die funksie in die geheel vreemd.
Waarskuwing
- Hierdie artikel is slegs van toepassing op funksies met twee veranderlikes, wat in `n tweedimensionele koördinaatstelsel geteken kan word.
Artikels oor die onderwerp "Weet of 'n funksie ewe of onewe is"
Оцените, пожалуйста статью
Soortgelyk
Gewilde