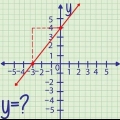
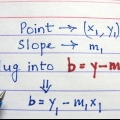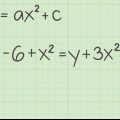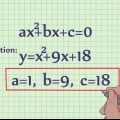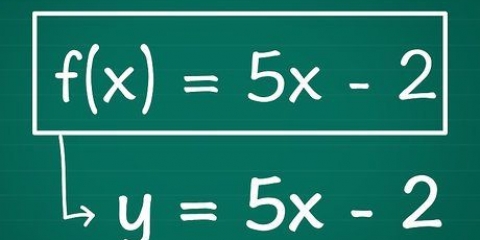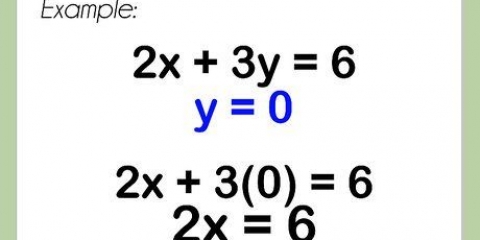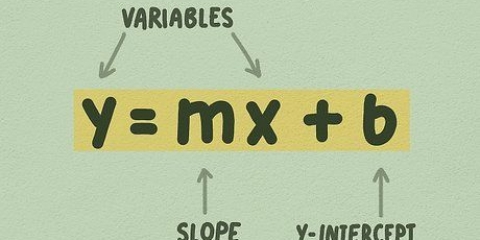Vir x = 2 is die punt op die kromme (2.27) want f(2) = 2^3 + 2*2^2 + 5*2 + 1 = 27. Vir f`(x) = 3x^2 + 4x + 5, is die helling in (2.27) is f`(2) = 3(2)^2 + 4(2) + 5 = 25. 
In die punt-helling vorm, is m die helling en (x1,y1) is die koördinate van die punt. So in hierdie voorbeeld word die vergelyking j - 27 = 25 (x - 2). 
Vind die vergelyking van 'n raaklyn
`n Raaklyn aan `n parabool of kromme is `n lyn wat slegs die kromme by `n gegewe punt raak. Om die vergelyking van hierdie raaklyn te vind, sal jy die helling van die kromme by daardie punt moet bereken, wat `n paar wiskundige berekeninge vereis. Jy kan dan die vergelyking van die raaklyn in `n punt-hellingsvorm skryf. Hierdie artikel verduidelik die stappe om te neem.
Trappe

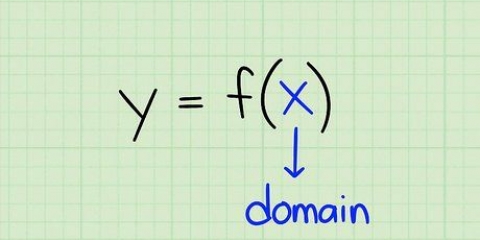
1. Die vergelyking van `n kromme kan as `n funksie uitgedruk word. Vind die afgeleide van hierdie funksie om die vergelyking van die helling van hierdie kromme te vind.
- Die maklikste manier om die meeste polinome te onderskei, is deur die kettingreël. Vermenigvuldig elke vergelyking van die funksie met sy mag om die koëffisiënt van daardie term in die afgeleide te vind, trek dan die mag af met 1.
- Voorbeeld: Vir die funksie f(x) = x^3 + 2x^2 + 5x + 1, is die afgeleide f`(x) = 3x^2 + 4x + 5.
- Vir f(x) = (2x+5)^10 + 2*(4x+3)^5, is die afgeleide f`(x) = 10*2*(2x+5)^9 + 2*5*4 *(4x+3)^4 = 20*(2x+5)^9 + 40*(4x+3)^4.

2. As alles goed is, word die koördinate gegee waar die raaklyn die kromme ontmoet. Prop in die x-waarde van hierdie punt, in die afgeleide funksie, om die helling van die kromme by daardie punt te vind.

3. Hierdie helling is ook die helling van die raaklyn. Nou het jy die helling en die punt van hierdie lyn, so jy kan die vergelyking van die lyn in punt-helling vorm skryf, of y - y1 = m(x - x1).

4. Dit kan ook nodig wees om hierdie vergelyking na `n ander vorm om te skakel om die finale antwoord te kry, sou die instruksies by die probleem dit vereis.
Artikels oor die onderwerp "Vind die vergelyking van 'n raaklyn"
Оцените, пожалуйста статью
Gewilde