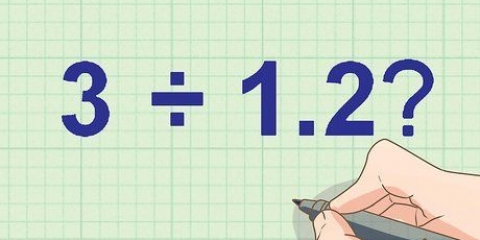Byvoorbeeld: die breuk  kan jy vereenvoudig om
kan jy vereenvoudig om  . Dus,
. Dus, 

Byvoorbeeld: omdat  , kan jy die eksponensiële uitdrukking herskryf as
, kan jy die eksponensiële uitdrukking herskryf as  .
. 
Byvoorbeeld:  .
. 
Byvoorbeeld: omdat ![Oplos van desimale eksponente 81^{{{frac{1}{4}}}}={sqrt[ {4}]{81}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b37415d73d383d0450962dda1cf0ddb2e0da0452) , kan jy die vergelyking herskryf as
, kan jy die vergelyking herskryf as ![Oplos van desimale eksponente ({sqrt[ {4}]{81}})^{{3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79a4e12743be369be81296fe2aeabd97c70cb9ab) .
. 
Byvoorbeeld: Om ![Oplos van desimale eksponente {sqrt[ {4}]{81}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44f5722ccf46fec0200534e84bda483bc2b726b1) om te bereken, moet jy bepaal watter getal vermenigvuldig met vier gelyk is aan 81. Omdat
om te bereken, moet jy bepaal watter getal vermenigvuldig met vier gelyk is aan 81. Omdat  , weet jy
, weet jy ![Oplos van desimale eksponente {sqrt[ {4}]{81}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/44d91764f62522cec7024ef6481f0b83305f17e9) . So word die eksponensiële vergelyking nou
. So word die eksponensiële vergelyking nou  .
. 
Byvoorbeeld:  . Dus,
. Dus,  .
. 

Die desimale  is gelyk aan
is gelyk aan  , Dus
, Dus  .
. 
Omdat  is vereenvoudig tot
is vereenvoudig tot  , tel dit
, tel dit  .
. As jy dit omskakel na `n onbehoorlike breuk, kry jy  . Dus,
. Dus,  .
. 






Byvoorbeeld:  .
. 
Byvoorbeeld:  .
. 
![Oplos van desimale eksponente x^{{{frac{1}{3}}}}={sqrt[ {3}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/759eade6ce89e27b301ccdcd83d7e8858827b8e2)
![Oplos van desimale eksponente x^{{{frac{1}{4}}}}={sqrt[ {4}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/625ea5fe7631555b2fc23ac21f595d7c20633ec9)
![Oplos van desimale eksponente x^{{{frac{1}{5}}}}={sqrt[ {5}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/788c8c448ea3cf9b81867b10ba6bbb1a47abb388)
Byvoorbeeld: ![Oplos van desimale eksponente 81^{{{frac{1}{4}}}}={sqrt[ {4}]{81}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/0af496f05893da79ec2c45b4ebebabce0930dce0) . Jy weet dat drie die vierde wortel van 81 is, want
. Jy weet dat drie die vierde wortel van 81 is, want 

As jy met vierkantsworteleksponente te doen het, dan word hierdie wet  , want
, want  .
.
Oplos van desimale eksponente
Inhoud
Die berekening van eksponente is `n basiese vaardigheid wat studente in pre-algebra aanleer. Gewoonlik sien jy eksponente as heelgetalle en soms sien jy hulle as breuke. Selde sien jy hulle as desimale. Wanneer `n eksponent as `n desimale getoon word, moet jy die desimale omskakeling na `n breuk. Vervolgens is daar `n paar reëls en wette rakende eksponente wat jy kan gebruik om die uitdrukking te bereken.
Trappe
Deel 1 van 3: Berekening van `n desimale eksponent

1. Skakel die desimale om na `n breuk. Om `n desimale na `n breuk om te skakel, moet jy die plekwaarde in ag neem. Die noemer van die breuk is die plekwaarde. Die syfers van die desimale punt is gelyk aan die teller.
- Byvoorbeeld: vir die eksponensiële uitdrukking
, moet jy
omskakel na `n breuk. Aangesien die desimale na die honderdstes plek gaan, is die ooreenstemmende breuk
.

2. Vereenvoudig die breuk, indien moontlik. Aangesien jy `n wortel skiet wat ooreenstem met die noemer van die breuk van die eksponent, wil jy hê die noemer moet so klein as moontlik wees. Doen dit vereenvoudiging van die breek. As die breuk `n gemengde getal is (d.w.Z. as jou eksponent `n desimale groter as 1 is), herskryf dit as `n onbehoorlike breuk.
 kan jy vereenvoudig om
kan jy vereenvoudig om  . Dus,
. Dus, 

3. Herskryf die eksponent as `n vermenigvuldiging. Jy doen dit deur die teller `n heelgetal te maak en dit met die stambreuk te vermenigvuldig. Die wortelbreuk is die breuk met dieselfde noemer, maar met 1 as die teller.
 , kan jy die eksponensiële uitdrukking herskryf as
, kan jy die eksponensiële uitdrukking herskryf as  .
.
4. Herskryf die eksponent as `n mag van `n mag. Onthou dat die vermenigvuldiging van twee eksponente dieselfde is as die mag van een mag. Dus  word
word  .
.
 word
word  .
. .
.
5. Herskryf die basis as `n vierkantswortelvergelyking. Om die eksponent van `n getal te bereken is gelykstaande aan die berekening van `n geskikte wortel van daardie getal. Herskryf dus die basis en die eerste eksponent as `n vierkantswortelvergelyking.
![Oplos van desimale eksponente 81^{{{frac{1}{4}}}}={sqrt[ {4}]{81}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b37415d73d383d0450962dda1cf0ddb2e0da0452) , kan jy die vergelyking herskryf as
, kan jy die vergelyking herskryf as ![Oplos van desimale eksponente ({sqrt[ {4}]{81}})^{{3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79a4e12743be369be81296fe2aeabd97c70cb9ab) .
.
6. Bereken die vierkantswortelvergelyking. Onthou dat die worteleksponent (die klein getal buite die radikaal) jou vertel watter wortel jy soek. As die getalle moeilik is, is dit die beste om dit te doen met die ![Oplos van desimale eksponente {sqrt[ {x}]{y}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58c28156258e3c4cf15e8af14abcc0163150e3e6) funksie op `n wiskunde sakrekenaar.
funksie op `n wiskunde sakrekenaar.
![Oplos van desimale eksponente {sqrt[ {x}]{y}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58c28156258e3c4cf15e8af14abcc0163150e3e6) funksie op `n wiskunde sakrekenaar.
funksie op `n wiskunde sakrekenaar.![Oplos van desimale eksponente {sqrt[ {4}]{81}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44f5722ccf46fec0200534e84bda483bc2b726b1) om te bereken, moet jy bepaal watter getal vermenigvuldig met vier gelyk is aan 81. Omdat
om te bereken, moet jy bepaal watter getal vermenigvuldig met vier gelyk is aan 81. Omdat  , weet jy
, weet jy ![Oplos van desimale eksponente {sqrt[ {4}]{81}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/44d91764f62522cec7024ef6481f0b83305f17e9) . So word die eksponensiële vergelyking nou
. So word die eksponensiële vergelyking nou  .
.
7. Bereken die oorblywende eksponent. Jy behoort nou `n heelgetal as `n eksponent te hê, dus moet die berekening anders eenvoudig wees. Jy kan altyd `n sakrekenaar gebruik as die getalle te groot is.
 . Dus,
. Dus,  .
.Deel 2 van 3: Los `n voorbeeldprobleem op

1. Bereken die volgende eksponensiële vergelyking: .
.
 .
.
2. Skakel die desimale om na `n breuk. Omdat  groter as 1 is, is die breuk `n gemengde getal.
groter as 1 is, is die breuk `n gemengde getal.
 groter as 1 is, is die breuk `n gemengde getal.
groter as 1 is, is die breuk `n gemengde getal. is gelyk aan
is gelyk aan  , Dus
, Dus  .
.
3. Vereenvoudig die breuk, indien moontlik. Jy moet ook enige gemengde getal na onbehoorlike breuke omskakel.
 is vereenvoudig tot
is vereenvoudig tot  , tel dit
, tel dit  .
. . Dus,
. Dus,  .
.
4. Herskryf die eksponent as `n vermenigvuldiging. Omdat  , kan jy die vergelyking herskryf as
, kan jy die vergelyking herskryf as  .
.
 , kan jy die vergelyking herskryf as
, kan jy die vergelyking herskryf as  .
.
5. Herskryf die eksponent as `n mag van `n mag. Dus,  .
.
 .
.
6. Herskryf die basis as `n vierkantswortelvergelyking.![Oplos van desimale eksponente 256^{{{frac{1}{4}}}}={sqrt[ {4}]{256}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb9c02c237d2aeb16bc1fd12eaf89cbde1d683a4) , wat jou toelaat om die vergelyking te herskryf as
, wat jou toelaat om die vergelyking te herskryf as ![Oplos van desimale eksponente ({sqrt[ {4}]{256}})^{{9}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/261990049bf6155622a73330e280af3d17084588) .
.
![Oplos van desimale eksponente 256^{{{frac{1}{4}}}}={sqrt[ {4}]{256}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb9c02c237d2aeb16bc1fd12eaf89cbde1d683a4) , wat jou toelaat om die vergelyking te herskryf as
, wat jou toelaat om die vergelyking te herskryf as ![Oplos van desimale eksponente ({sqrt[ {4}]{256}})^{{9}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/261990049bf6155622a73330e280af3d17084588) .
.
7. Bereken die vierkantswortelvergelyking.![Oplos van desimale eksponente {sqrt[ {4}]{256}}=4](https://wikimedia.org/api/rest_v1/media/math/render/svg/55bb3e8f3f86ce5c35d5f18ddd8f486e75e67476) . So die vergelyking is nou
. So die vergelyking is nou  .
.
![Oplos van desimale eksponente {sqrt[ {4}]{256}}=4](https://wikimedia.org/api/rest_v1/media/math/render/svg/55bb3e8f3f86ce5c35d5f18ddd8f486e75e67476) . So die vergelyking is nou
. So die vergelyking is nou  .
.
8. Bereken die oorblywende eksponent. . Dus,
. Dus,  .
.
 . Dus,
. Dus,  .
.Deel 3 van 3: Verstaan eksponente

1. Herken `n eksponensiële vergelyking. `n Eksponensiële vergelyking het `n basis en `n eksponent. Die basis is die groter getal in die vergelyking. Die eksponent is die kleiner getal.
- Byvoorbeeld: in die vergelyking
, is
die basis en
die eksponent.

2. Herken die dele van `n eksponensiële vergelyking. Die basis is die getal wat vermenigvuldig word. Die eksponent dui aan hoe gereeld die basis as `n faktor in die vergelyking gebruik word.
 .
.
3. Herken `n vierkantsworteleksponent. `n Vierkantsworteleksponent kan ook `n breukeksponent genoem word. Dit is `n eksponent in die vorm van `n breuk.
 .
.
4. Verstaan die verband tussen vierkantswortel- en vierkantsworteleksponente. Die Verheerliking  van `n getal is soos die vierkantswortel van daardie getal. Dus,
van `n getal is soos die vierkantswortel van daardie getal. Dus,  . Dieselfde geld vir ander wortels en eksponente. Die noemer van die eksponent sê vir jou watter wortel om te neem:
. Dieselfde geld vir ander wortels en eksponente. Die noemer van die eksponent sê vir jou watter wortel om te neem:
 van `n getal is soos die vierkantswortel van daardie getal. Dus,
van `n getal is soos die vierkantswortel van daardie getal. Dus,  . Dieselfde geld vir ander wortels en eksponente. Die noemer van die eksponent sê vir jou watter wortel om te neem:
. Dieselfde geld vir ander wortels en eksponente. Die noemer van die eksponent sê vir jou watter wortel om te neem:![Oplos van desimale eksponente x^{{{frac{1}{3}}}}={sqrt[ {3}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/759eade6ce89e27b301ccdcd83d7e8858827b8e2)
![Oplos van desimale eksponente x^{{{frac{1}{4}}}}={sqrt[ {4}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/625ea5fe7631555b2fc23ac21f595d7c20633ec9)
![Oplos van desimale eksponente x^{{{frac{1}{5}}}}={sqrt[ {5}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/788c8c448ea3cf9b81867b10ba6bbb1a47abb388)
![Oplos van desimale eksponente 81^{{{frac{1}{4}}}}={sqrt[ {4}]{81}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/0af496f05893da79ec2c45b4ebebabce0930dce0) . Jy weet dat drie die vierde wortel van 81 is, want
. Jy weet dat drie die vierde wortel van 81 is, want 

5. Verstaan die eksponensiële wet van mag van `n mag. Hierdie wet bepaal dat  . Met ander woorde, om `n eksponent tot mag te verhoog, is dieselfde as om twee eksponente te vermenigvuldig.
. Met ander woorde, om `n eksponent tot mag te verhoog, is dieselfde as om twee eksponente te vermenigvuldig.
 . Met ander woorde, om `n eksponent tot mag te verhoog, is dieselfde as om twee eksponente te vermenigvuldig.
. Met ander woorde, om `n eksponent tot mag te verhoog, is dieselfde as om twee eksponente te vermenigvuldig. , want
, want  .
.Artikels oor die onderwerp "Oplos van desimale eksponente"
Оцените, пожалуйста статью
Soortgelyk
Gewilde