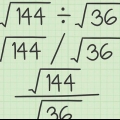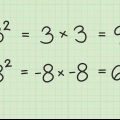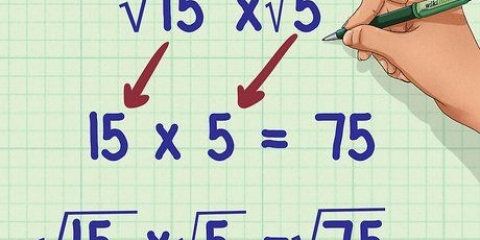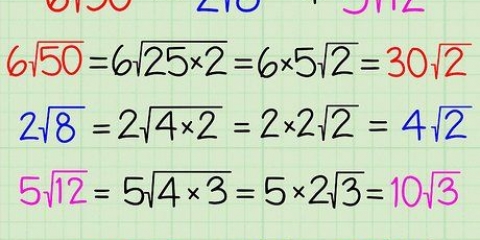Vereenvoudig vierkantswortels
Inhoud
Om `n vierkantswortel te vereenvoudig is nie so moeilik soos dit lyk nie. Om `n vierkantswortel te vereenvoudig, moet jy net die getal van die vierkantswortel faktoriseer en probeer om die vierkantswortel van een of albei faktore te neem. Sodra jy `n paar algemene vierkantgetalle ken en weet hoe om `n getal in faktore te verdeel, is jy goed op pad om `n vierkantswortel te vereenvoudig. Hier is hoe jy dit vinnig kan leer.
Trappe
Metode 1 van 4: Vereenvoudig die vierkantswortel van `n getal

1. Leer `n paar vierkantgetalle en hul wortels. Kwadratering, deur `n getal met homself te vermenigvuldig, maak `n kwadraatgetal (volmaak kwadraat). Byvoorbeeld: 25 is `n getal gekwadraat omdat 5 x 5, of 5, gelyk is aan 25. Om ten minste die eerste 10 tien kwadraatgetalle te ken, kan help om vierkantswortels te herken en te vereenvoudig. Hier is die eerste tien kwadraatgetalle:
- 1 = 1
- 2 = 4
- 3 = 9
- 4 = 16
- 5 = 25
- 6 = 36
- 7 = 49
- 8 = 64
- 9 = 81
- 10 = 100

2. Vind die vierkantswortel van `n vierkantsgetal. As jy `n vierkantsgetal onder `n radikaal sien, moet jy net die radikaal (√ ) verwyder en die vierkantswortel van die vierkantsgetal skryf. As jy dit al uit jou kop geleer het, dan is jy klaar. As die getal te groot is en jy nie seker is of dit `n vierkantsgetal is nie, probeer om die vierkantswortel met jou sakrekenaar te vind om te kyk of dit `n mooi ronde getal lewer. Byvoorbeeld: by √25 weet jy dat die antwoord gelyk is aan 5 want 25 is `n getal kwadraat.
Metode 2 van 4: Vereenvoudig `n vierkantswortel deur faktorisering

1. As die getal ewe is, deel dit deur 2. Om die faktore van `n getal te vind behels die vind van alle getalle wat saam vermenigvuldig daardie getal produseer, wat dit makliker maak om sy vierkantswortel te bepaal. As dit `n ewe getal is, is die eerste ding wat jy kan doen om die getal deur 2 te deel. In hierdie voorbeeld kan jy √98 verdeel in √(2x49), want 98 : 2 =49. As die getal nie deur 2 deelbaar is nie, probeer 3, 4, 5, ensovoorts totdat jy die regte kombinasie kry.

2. Verdeel hierdie faktore terug in faktore om verdere vierkantgetalle te vind. Kyk of jy kan aanhou om die getal in faktore te verdeel. 2 is priem en het slegs homself en 1 as deler. Maar 49, die ander faktor, kan steeds in 7 x 7 verdeel word, want dit is `n vierkantige getal. So jy kan die wortel √(2x49) herskryf as √(2x7x7), of √[2(7)], wat beteken dat ons reeds die vierkantsgetal waarna ons gesoek het gevind het.

3. Vereenvoudig die vierkantswortel. Aangesien √98= √[2(7)], is dit moontlik om `n 7 buite die radikaal te plaas en die antwoord na 7√2 te vereenvoudig. Dus √49 of ook (7 x 7), word dan 7 sodra jy dit buite die radikaal plaas. As jy die 7 weer terug plaas, word dit weer `n vierkantige getal en dus 49. Dus, √98 = 7√2.
Metode 3 van 4: Ander metodes om `n vierkantswortel te vereenvoudig
1. As jy nie dadelik daarin slaag om `n vierkantige getal te vind nie, deel dan die getal verder. Byvoorbeeld, as die probleem √48 is, gaan jy voort om te deel totdat jy nie verder as 2x2 kan gaan nie, sodat 4 `n koëffisiënt van die radikaal word en 3 binne die radikaal bly. Hier is hoe dit werk:
- √48 = √(2 x 24)
- √(2 x 24) = √(2 x 12 x 2)
- √(2 x 12 x 2) = √(2 x 6 x 2 x 2)
- √(2 x 6 x 2 x 2) = √(2 x 3 x 2 x 2 x 2)
- √(2 x 3 x 2 x 2 x 2) = √(2 x 3)
- √(2 x 3)= 4√3
- √48 = 4√3
2. Onthou jy kan nie `n priemgetal vereenvoudig nie. Dit is omdat die faktore hier 1 en die priemgetal self is. Byvoorbeeld: √17 kan nie vereenvoudig word nie, want 17 is priemgetal.
3. Verdeel in faktore van meer as een kwadraatgetal. As die faktore van die getal meer as een vierkante getal bevat, neem hulle almal buite die radikaal. As jy verskeie vierkante gevind het terwyl jy vereenvoudig het, neem hulle almal buite die radikaal en vermenigvuldig hulle. Byvoorbeeld: Kom ons neem aan dat jy die getal √32 wil vereenvoudig, verdeel dit dan in die faktore 4 x 4 x 2, en let op dat die vierkant getal 4 twee keer voorkom. Maak hierdie 16√2 wat uiteindelik 4√2 sal oplewer.
4. Moenie die koëffisiënt met `n hoër kragwortel verwar nie. 3√125, byvoorbeeld, is gelyk aan 3 x √125, maar √125 is die derdemagswortel van 125. (want 5 x 5 x 5 = 125, √125 = 5.)
Metode 4 van 4: Ken die terminologie

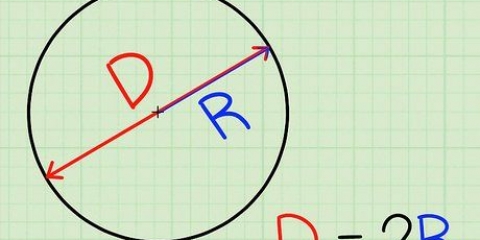
1. Onthou dat die radikaal (√) die simbool vir die vierkantswortel is. Byvoorbeeld, in die probleem √25, "√" die radikale teken.

2. Onthou dat die radikaal die getal onder die radikaal is. Vind die vierkantswortel van hierdie getal. Byvoorbeeld: by √25 is "25" die wortelgetal.

3. Onthou dat die koëffisiënt die getal buite die radikaal is. Hierdie getal vermenigvuldig die vierkantswortel; Dit kan gevind word aan die linkerkant van die radikale teken, die √-simbool. Byvoorbeeld: by 7√2, "7" die koëffisiënt.

4. Onthou dat `n faktor `n getal is wat heeltemal in `n ander getal ingaan. Byvoorbeeld: 2 is `n faktor van 8 omdat 8 ÷ 4 = 2, maar 3 is nie `n faktor van 8 nie omdat 8÷3 nie `n heelgetal beantwoord nie. Byvoorbeeld: 5 is `n faktor van 25 omdat 5 x 5 = 25.

5. Verstaan die betekenis van die vereenvoudiging van `n vierkantswortel. Om `n vierkantswortel te vereenvoudig, behels bloot die verdeling van `n vierkant van `n vierkantswortel in faktore, en dan na links van die radikaal te skuif, en die ander faktor binne die radikaal te laat. As die getal `n vierkantsgetal is, kan jy die radikale teken verwyder sodra jy sy vierkantswortel geskryf het. Byvoorbeeld: √98 kan na 7√2 vereenvoudig word.
Wenke
- Een manier om vierkante te vind om jou kwadraatgetalle te deel, is om vierkante in jou lys op te soek wat begin met die kleinste getal na jou kwadraatgetal. Byvoorbeeld: as jy die vierkantgetal van 27 soek, begin by 25 en stop by 9, want jy het die grootste deler gevind wat ’n vierkantgetal is.
Waarskuwings
- Moenie sakrekenaars gebruik nie, behalwe in die stap waar jy probeer uitvind hoeveel keer die vierkant in die vierkantswortel gaan.
- Vereenvoudiging is nie dieselfde as om waardes in `n vergelyking te plaas nie.Nêrens in die hele proses kan `n desimale getal nêrens verskyn nie!
Artikels oor die onderwerp "Vereenvoudig vierkantswortels"
Оцените, пожалуйста статью
Gewilde