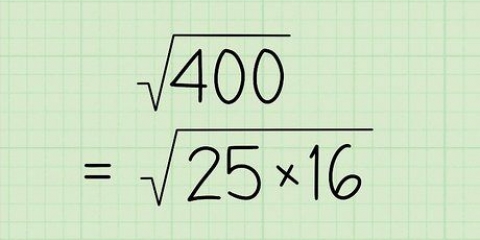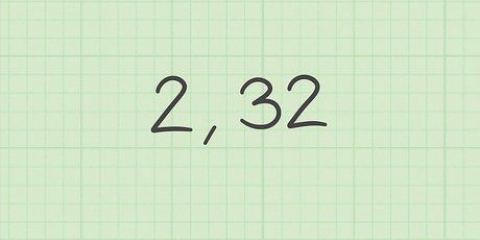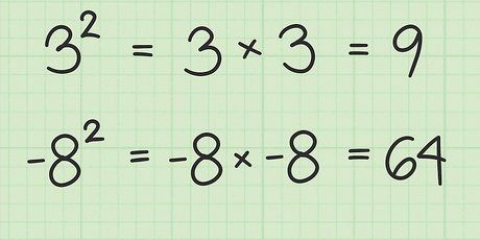Vereenvoudig wortels

1. Vereenvoudig enige wortel wat ook `n vierkantsgetal is. `n Getal gekwadraat is die produk van enige getal met homself soos 81, wat die produk van 9 x 9 is. Om `n wortel van hierdie vorm te vereenvoudig, hoef jy net die radikaal te verwyder en die wortel van die vierkant te skryf.

• Byvoorbeeld, 121 is `n getal gekwadraat, want 11 x 11 is gelyk aan 121. Jy kan die radikaal maklik verwyder en 11 as jou antwoord skryf.
• Om hierdie proses makliker te maak, is dit nuttig om die eerste twintig vierkante getalle te memoriseer: 1 x 1 = 1, 2 x 2 = 4, 3 x 3 = 9, 4 x 4 = 16,5 x 5 = 25, 6 x 6 = 36,7 x 7 = 49, 8 x 8 = 64,9 x 9 = 81, 10 x 10 = 100, 11 x 11 = 121, 12 x 12 = 144, 13 x 13 = 169, 14 x 14 = 196, = 5 x 1, 5 225, 16 x 16 = 256, 17 x 17 = 289, 18 x 18 = 324, 19 x 19 = 361, 20 x 20 = 400

Metode 2 van 5: Die kubusnommer

1. Vereenvoudiging van kubusgetalle. `n Kubusgetal is die produk van enige getal vermenigvuldig met homself twee keer, soos 27 wat die produk is van 3 x 3 x 3. Om `n wortel met `n derdemagsgetal onder die radikaal te vereenvoudig, moet jy net hierdie teken verwyder en die derdemagswortel van die getal skryf.

• Byvoorbeeld: Die produk van 8 x 8 x 8 is gelyk aan die kubusgetal 512. Daarom is die derdemagswortel van 512 gelyk aan 8.

Metode 3 van 5: Ander getalle

1. Verdeel `n wortelgetal in faktore. Faktore is daardie getalle wat saam vermenigvuldig `n sekere produk vorm -- byvoorbeeld, 5 en 4 is twee faktore van die produk 20. Om `n wortelgetal te faktoriseer, skryf al die faktore van daardie getal (of soveel as wat jy dink daar is, as dit `n groot getal is) neer totdat jy een vind wat `n kwadraatgetal is.

• `n Voorbeeld, `n lys van alle faktore van die getal 45: 1, 3, 5, 9, 15 en 45. 9 is `n faktor van 45 en dit is ook `n getal in die kwadraat. 9 x 5 = 45.

2. Verwyder enige faktor wat `n vierkante getal is van die radikaal. 9 is `n vierkantige getal want 9 is die produk van 3 x 3. Verwyder 9 van die radikaal en plaas `n 3 voor dit, laat 5 onder die radikaal. 3 vierkantswortel 5 is net `n vereenvoudigde weergawe van vierkantswortel 45.

1. Vind `n vierkantige getal in die veranderlike. Die vierkantswortel van a is gelyk aan a. Die vierkantswortel van akan in die wortel van gebreek word aete a – Dit is die geval omdat jy eksponente bymekaar tel wanneer jy veranderlikes saam vermenigvuldig.aete a is gelyk aan a.

• Dus is die getal in die kwadraat van die uitdrukking a gelyk aan a.

2. Verwyder alle veranderlikes wat gelyk is aan `n vierkantige getal van die radikaal. kom ons nou a neem dit en onttrek dit uit die radikale wat dit `n gereelde veranderlike maak a word. Die vereenvoudigde vorm van a is net a wortel a.

1. Vereenvoudig `n vierkantswortel met veranderlikes en getalle. Om dit te doen, verdeel eenvoudig die uitdrukking deur eers vir vierkante in die getalle te soek en dan in die veranderlikes. Verwyder dan die radikale teken en los die vierkantswortels. Kom ons kyk na die vierkantswortel van 36 x a.

• 36 is `n vierkantige getal want 6 x 6 is 36.
  
  
• a is `n vierkantige getal omdat a ete a is a.
• Noudat jy hierdie getalle en veranderlikes in hul vierkantswortels opgebreek het, verwyder die radikaal en los die vierkantswortels. Die vierkantswortel van 36 x a is 6a.

2. Vereenvoudig `n vierkantswortel met veranderlikes en getalle. Verdeel die uitdrukking in getalle en veranderlikes en soek vierkante in die faktore van albei. Onttrek dan elke vierkantsgetal uit die vierkantswortelvergelyking. Kom ons kyk wat ons met die vierkantswortel van 50 x kan doen a.