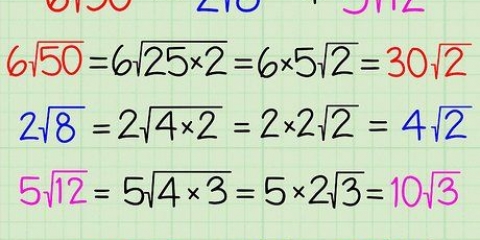Vermenigvuldig wortelgetalle

Inhoud

Trappe
Wenke

Die wortelsimbool (√) verteenwoordig die vierkantswortel van `n getal. Jy kan die wortelsimbool in wiskunde teëkom, of selfs in skrynwerk of enige ander veld waar meetkunde ter sprake kom of wanneer relatiewe afmetings of afstande bereken word. Jy kan wortels vermenigvuldig wat dieselfde krag het (kragwortels). As radikale nie dieselfde krag het nie, kan jy hul vergelyking wysig totdat hulle dit het. As jy wil weet hoe om wortels met of sonder koëffisiënte te vermenigvuldig, volg die stappe hieronder.

Trappe

Metode 1 van 3: Vermenigvuldiging van wortels sonder koëffisiënte

Prent getiteld Vermenigvuldig Radikale Stap 1

1. Maak seker dat die wortels dieselfde krag het. Om wortels met die basiese metode te vermenigvuldig, moet hulle dieselfde krag hê. Die `krag` is die klein geskrewe getal links van die boonste reël van die wortelsimbool. As geen mag gespesifiseer is nie, het jy te doen met `n vierkantswortel (tweede mag) en dit kan vermenigvuldig word met ander vierkantswortels. Jy kan wortels van verskillende magte saam vermenigvuldig, maar dit is `n gevorderde metode en sal later verduidelik word. Hier is twee voorbeelde van vermenigvuldiging van wortels met dieselfde magte:

Bv. 1: √(18) x √(2) = ?
Bv. 2: √(10) x √(5) = ?
Bv. 3: √(3) x √(9) = ?

Prent getiteld Vermenigvuldig Radikale Stap 2

2. Vermenigvuldig die getalle onder die radikaal. Dan vermenigvuldig jy die getalle onder die radikale teken en laat dit daar. Dit gaan so:

Bv. 1: √(18) x √(2) = √(36)

Bv. 2: √(10) x √(5) = √(50)

Bv. 3: √(3) x √(9) = √(27)

Prent getiteld Vermenigvuldig Radikale Stap 3

3. Vereenvoudig die wortels. Sodra jy die wortels vermenigvuldig het, is daar `n goeie kans dat hulle tot `n perfekte vierkant of krag van twee vereenvoudig kan word, of hulle kan vereenvoudig word deur `n vierkant te vind as `n faktor van die finale produk. Jy doen dit soos volg:

Bv. 1: √(36) = 6. 36 is `n vierkant omdat dit `n produk van 6 x 6 is. Die vierkantswortel van 36 is net 6.

Bv. 2: √(50) = √(25 x 2) = √([5 x 5] x 2) = 5√(2). Terwyl 50 nie `n vierkantgetal is nie, is 25 `n faktor van 50 (want dit pas presies twee keer) en is `n perfekte vierkant. Jy kan faktor 25 (5 x 5) en plaas `n 5 buite die radikaal om die vergelyking te vereenvoudig.

Jy kan so daaroor dink: As jy die 5 weer onder die radikale teken plaas, sal dit vanself vermenigvuldig en weer 25 word.

Bv. 3:√(27) = 3. 27a is `n perfekte kubus (derde mag), want dit is die produk van 3 x 3 x 3. Die vierkantswortel van 27 is dus 3.

Metode 2 van 3: Vermenigvuldig wortels met koëffisiënte

Prent getiteld Vermenigvuldig Radikale Stap 4

1. Vermenigvuldig die koëffisiënte. Die koëffisiënte is die getalle buite die radikaal. As geen koëffisiënt gegee word nie, kan jy die koëffisiënt as 1 beskou. Vermenigvuldig die koëffisiënte saam. Jy doen dit soos volg:

Bv. 1: 3√(2) x √(10) = 3√( ? )

3 x 1 = 3

Bv. 2: 4√(3) x 3√(6) = 12√( ? )

4 x 3 = 12

Prent getiteld Vermenigvuldig Radikale Stap 5

2. Vermenigvuldig die getalle binne die wortels. Nadat jy die koëffisiënte vermenigvuldig het, kan jy begin om die getalle binne die wortels te vermenigvuldig. Jy doen dit soos volg:

Bv. 1: 3√(2) x √(10) = 3√(2 x 10) = 3√(20)

Bv. 2: 4√(3) x 3√(6) = 12√(3 x 6) = 12√(18)

Prent getiteld Vermenigvuldig Radikale Stap 6

3. Vereenvoudig die produk. Dan vereenvoudig jy die getalle onder die wortels deur te soek na die perfekte vierkante of veelvoude van die getalle onder die wortels waaruit perfekte vierkante bestaan. Sodra jy daardie terme vereenvoudig het, vermenigvuldig hul ooreenstemmende koëffisiënte met. Jy doen dit soos volg:

3√(20) = 3√(4 x 5) = 3√([2 x 2] x 5) = (3 x 2)√(5) = 6√(5)

12√(18) = 12√(9 x 2) = 12√(3 x 3 x 2) = (12 x 3)√(2) = 36√(2)

Metode 3 van 3: Vermenigvuldig verskillende magswortels

Prent getiteld Vermenigvuldig Radikale Stap 7

1. Vind die LCF (Least Common Multiple) van die magte. Om die LCF van die magte te vind, vind die kleinste getal wat deur beide magte deelbaar is. Vind die LCF van die indekse vir die volgende vergelyking: √(5) x √(2) = ?

Die indekse is 3 en 2. 6 is die LCF van hierdie twee getalle, want dit is die kleinste getal wat deelbaar is deur beide 3 en 2. 6/3 = 2 en 6/2 = 3. Om die wortels te vermenigvuldig, moet albei magte 6 wees.

Prent getiteld Vermenigvuldig Radikale Stap 8

2. Skryf elke uitdrukking met die nuwe LCF as die mag. Die uitdrukkings sal so lyk in vergelyking met hul nuwe kragte:

√(5) x √(2) = ?

Prent getiteld Vermenigvuldig Radikale Stap 9

3. Vind die getal waarmee jy elk van die oorspronklike magte moet vermenigvuldig om die LCF te bepaal. Met die uitdrukking √(5) sal jou krag van 3 met 2 vermenigvuldig moet word om 6 te kry. Met die uitdrukking √(2) sal jy mag 2 met 3 moet vermenigvuldig om 6 te kry.

Prent getiteld Vermenigvuldig Radikale Stap 10

4. Maak hierdie getal die eksponent van die getal binne die vierkantswortel. In die eerste vergelyking word 2 die mag van 5. In die tweede vergelyking word 3 die mag van 2. Dit sal so lyk:

--> √(5) = √(5)

--> √(2) = √(2)

Prent getiteld Vermenigvuldig Radikale Stap 11

5. Vermenigvuldig die getalle binne die wortels met hul eksponente. Jy doen dit soos volg:

√(5) = √(5 x 5) = √25

√(2) = √(2 x 2 x 2) = √8

Prent getiteld Vermenigvuldig Radikale Stap 12

6. Plaas hierdie getalle onder een radikaal. Plaas hulle onder `n radikale teken en verbind hulle met `n vermenigvuldigingsteken. Dit is hoe die resultaat lyk: √(8 x 25)

Prent getiteld Vermenigvuldig Radikale Stap 13

7. Vermenigvuldig. √(8 x 25) = √(200). Dit is die finale antwoord. In sommige gevalle kan jy dalk hierdie uitdrukkings selfs meer vereenvoudig -- byvoorbeeld, as jy `n getal kan vind wat ses keer met homself vermenigvuldig 200 produseer. Maar dit is nie moontlik nie, wat beteken dat die uitdrukking nie verder vereenvoudig kan word nie.

Wenke

As daar `n plus- of minusteken tussen `n getal en die radikaal is, dan is dit nie `n koëffisiënt nie - in welke geval dit `n aparte term is en apart van die radikaal behandel moet word. As `n radikale en `n ander term tussen hakies ingesluit is -- byvoorbeeld, (2 + √5), dan moet jy beide 2 en √5 afsonderlik behandel wanneer bewerkings binne die hakies uitgevoer word, maar wanneer bewerkings buite die hakies uitgevoer word, moet jy beskou (2 + √5) as een geheel.
Worteltekens is `n ander manier om fraksionele eksponente uit te druk. Met ander woorde, die vierkantswortel van `n getal is dieselfde as daardie getal verhoog tot die 1/2 mag, die derdemagswortel van enige getal is dieselfde as daardie getal verhoog tot die 1/3 mag, ensovoorts.
A "koëffisiënt" is die getal (as daar `n getal is) onmiddellik voor die radikaal. Dus in die uitdrukking 2√5 is 5 onder die radikaal en die getal 2 (buite die radikaal) is die koëffisiënt. Wanneer `n wortel en `n koëffisiënt as `n groep voorgestel word, beteken dit dat die wortel en die koëffisiënt met mekaar vermenigvuldig moet word, soos in die voorbeeld: 2 * √5.