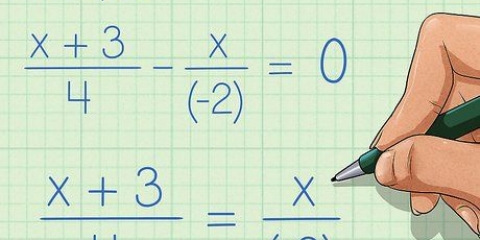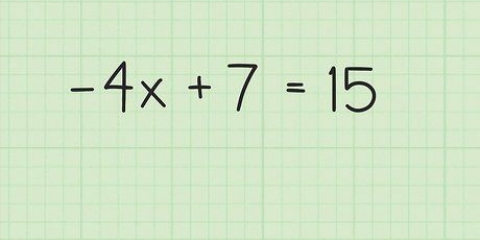Kruisvermenigvuldiging: 8 stappe (met prente)

Inhoud

Trappe
- Metode 1 van 2: Kruisvermenigvuldiging met een veranderlike
- Metode 2 van 2: Kruisvermenigvuldiging met veelvuldige veranderlikes
Wenke

Kruisvermenigvuldiging is `n manier om `n vergelyking op te los, met `n veranderlike as deel van twee breuke wat gelyk is aan mekaar. Die veranderlike is `n onbekende getal of hoeveelheid, en kruisvermenigvuldiging maak hierdie breukvergelyking `n eenvoudige vergelyking, wat jou toelaat om vir die betrokke veranderlike op te los. Kruisvermenigvuldiging is veral nuttig wanneer `n verhouding probeer oplos word. Hier is hoe om dit te doen.

Trappe

Metode 1 van 2: Kruisvermenigvuldiging met een veranderlike

1. Vermenigvuldig die teller van die linkerbreuk met die noemer van die regterbreuk. Kom ons sê jy werk aan die vergelyking 2/x = 10/13. Vermenigvuldig nou 2 met 13. 2 x 13 = 26.

2. Vermenigvuldig die teller van die regterbreuk met die noemer van die linkerbreuk. Vermenigvuldig met 10. x * 10 = 10x. Jy kan eers vermenigvuldig in hierdie rigting kruis; dit maak op die ou end nie saak nie, solank jy albei tellers vermenigvuldig met die diagonale noemers van die ander breuk.

3. Maak die twee produkte gelyk aan mekaar. Maak 26 gelyk aan 10x. 26 = 10x. Dit maak nie saak watter nommer jy eerste neem nie; omdat hulle ekwivalent is, kan jy hulle sonder enige gevolge van die een kant van die vergelyking na die ander skuif; as jy elke kwartaal as `n geheel behandel.

So as jy probeer om vir 2/x = 10/13 vir x op te los, kry jy 2 * 13 = x * 10, of 26 = 10x.

4. Los op vir die veranderlike. Noudat jy met 26 = 10x te doen het, kan jy begin om die gemene deler te vind deur beide 26 en 10 te deel deur `n getal wat albei noemers deelbaar het deur. Aangesien hulle albei ewe getalle is, is dit moontlik om hulle deur 2 te deel; 26/2 = 13 en 10/2 = 5. Nou bly jy oor met 13 = 5x as `n vergelyking. Om x te isoleer, deel dan beide kante van die vergelyking deur 5. Dus 13/5 = 5/5, of 13/5 = x. As jy die antwoord as `n desimale breuk of desimale wil hê, kan jy beide kante van die vergelyking deur 10 deel om 26/10 = 10/10, of 2 te kry.6 = x.

Metode 2 van 2: Kruisvermenigvuldiging met veelvuldige veranderlikes

1. Vermenigvuldig die teller van die linkerbreuk met die noemer van die regterbreuk. Kom ons sê jy werk aan die volgende vergelyking: (x + 3)/2 = (x + 1)/4. Vermenigvuldig (x + 3) van 4 aan 4(x +3) te kry. Dit word uitgewerk 4x + 12.

2. Vermenigvuldig die teller van die regterbreuk met die noemer van die linkerbreuk. Herhaal hierdie prosedure aan die ander kant. (x+1) x 2 = 2(x +1). Dit word dan 2(x +1) 2x + 2.

3. Maak die twee produkte gelyk aan mekaar en kombineer gelyke terme. Nou het jy 4x + 12 = 2x + 2. Kombineer die X terme en die konstantes aan beide kante van die vergelyking.

So, kombineer 4x en 2x deur middel van 2x trek van beide kante van die vergelyking af. Uitgewerk, dit lewer die volgende vergelyking 2x + 12 = 2.

Kombineer nou 12 en 2 deur middel van 12 trek van beide kante van die vergelyking af. Uitgewerk lyk dit so: 2x + 12-12 = 2-12.

Dus word die vergelyking: 2x = -10.

4. Los op. Al wat jy nou moet doen is om beide kante van die vergelyking te deel deur 2. 2x/2 = -10/2 = x = -5. Na kruisvermenigvuldiging sal jy sien dat x = -5. Jy kan teruggaan en seker maak dat alles korrek is deur -5 vir x in te voer om seker te maak beide kante van die vergelyking is gelyk. Die resultaat van hierdie kontrole is -1 = -1, en dit is waar omdat beide kante van die vergelyking gelyk is. Sou die beheer bv. 0 = -1 gee terug die vergelyking is nie korrek nie, so iets het verkeerd geloop.

Wenke

Let daarop dat as jy `n ander getal (byvoorbeeld 5) in dieselfde vergelyking invoer, jy die volgende resultaat kry: 2/5 = 10/13. Selfs as jy die linkerkant van die vergelyking weer met 5/5 vermenigvuldig, kry jy 10/25 = 10/13, wat duidelik verkeerd is. Hierdie laaste geval wys duidelik dat jy `n fout gemaak het met kruisvermenigvuldiging.