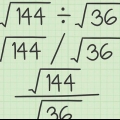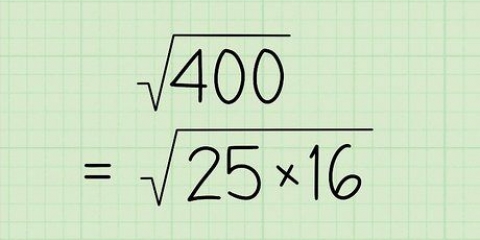Nog `n voorbeeld: Ons wil die vierkantswortel van 25 vind (√(25)). Dit beteken ons moet die getal vind wat vermenigvuldig met homself 25 as die produk het. Aangesien 5 = 5 × 5 = 25, kan ons sê dat √(25) = 5. Jy kan ook hieraan dink as die "ongedoen" van `n vierkant (of maggetal). Byvoorbeeld, as ons die vierkantswortel van 64 (√64) wil vind, beskou 64 as 8 . Aangesien `n radikaal in beginsel `n vierkant `uitskakel`, kan ons sê dat √(64) = √(8) = 8. 
Aan die ander kant word getalle genoem wat nie heelgetalle na vierkantswortel gee nie, onvolmaakte vierkant. Wanneer jy die vierkantswortel van een van hierdie getalle neem, kry jy gewoonlik `n desimale of breuk. Soms kan die betrokke desimale baie deurmekaar raak. Byvoorbeeld, √(13) = 3,605551275464 … 
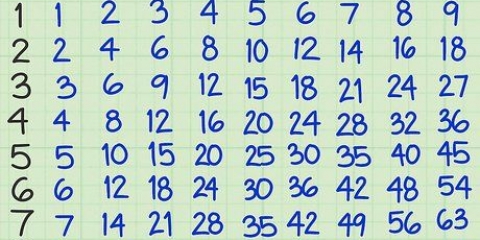
1 = 1 × 1 = 1 2 = 2 × 2 = 4 3 = 3 × 3 = 9 4 = 4 × 4 = 16 5 = 5 × 5 = 25 6 = 6 × 6 = 36 7 = 7 × 7 = 49 8 = 8 × 8 = 64 9 = 9 × 9 = 81 10 = 10 × 10 = 100 11 = 11 × 11 = 121 12 = 12 × 12 = 144 
Gestel jy wil die vierkantswortel van 900 bereken. Met die eerste oogopslag lyk dit baie moeilik! Dit is egter nie moeilik as ons 900 faktoriseer nie. `Faktore` is daardie getalle wat saam kan vermenigvuldig om `n ander getal te maak. Byvoorbeeld, aangesien 6 die produk van 1 × 6 en 2 × 3 is, is die faktore van 6 die getalle 1, 2, 3 en 6. In plaas daarvan om met die getal 900 te bereken, wat `n bietjie ongerieflik is, skryf ons dit as 9 × 100. Nou, aangesien 9 `n perfekte vierkant is en geskei van 100, kan ons sy vierkantswortel neem. √(9 × 100) = √(9) × √(100) = 3 × √(100). Met ander woorde, √(900) = 3√(100). Ons kan hierdie twee stappe nog verder vereenvoudig deur 100 in die faktore 25 en 4 te deel. √(100) = √(25 × 4) = √(25) × √(4) = 5 × 2 = 10. Ons kan dus sê dat √(900) = 3(10) = 30. 
Let wel: Alhoewel denkbeeldige getalle nie met gereelde getalle voorgestel kan word nie, kan hulle steeds op baie maniere as gereelde getalle behandel word. Byvoorbeeld, die wortels van negatiewe getalle kan kwadraat gemaak word om daardie negatiewe getalle net soos enige ander vierkantswortel te gee. Byvoorbeeld: i = -1. 

In ons voorbeeld verdeel ons 6.45 in pare soos volg: 6-,45-00. Let daarop dat daar `n `oorblywende` nommer aan die linkerkant is &mdash dit is die punt. 
In ons voorbeeld is die eerste groep in 6-,45-00 die 6. Die grootste getal kleiner as of gelyk aan 6 is 2 — 2 = 4. Skryf `n `2` bo die 6 onder die radikaal. 
In ons voorbeeld begin ons met die dubbel van 2, die eerste syfer van ons antwoord. 2 × 2 = 4. Dan trek ons 4 van 6 af (ons eerste `groep`) en ons kry 2 as `n antwoord. Dan skuif ons die volgende groep (45) een lyn af om 245 te kry. Ten slotte skryf ons nog 4 aan die linkerkant, laat `n bietjie spasie aan die einde by, soos volg: 4_. 
In ons voorbeeld soek ons die nommer om die leë in te vul in 4_ × _; dit maak die antwoord so groot as moontlik, maar steeds minder as of gelyk aan 245. In hierdie geval is die antwoord 5. 45 × 5 = 225, terwyl 46 × 6 = 276. 
Ons gaan voort met ons voorbeeld en gaan voort met 225 - 245 = 20. Dan bring ons die volgende paar syfers, 00, af om 2000 te maak. As ons die getal bokant die radikaal verdubbel, kry ons 25 × 2 = 50. Ons los die onbekende op in 50_ × _ =/< 2000, dan kry ons 3 as antwoord. Op hierdie punt het ons `253` bokant die radikale - as jy dit weer herhaal, is 9 die volgende syfer. 
In ons voorbeeld is die getal onder die radikale teken 6,45, so ons skuif eenvoudig die desimale punt op en plaas dit tussen 2 en 5 van ons antwoord, wat ons gee 2 539 opbrengste. 

In ons voorbeeldprobleem is `n redelike skatting vir die vierkantswortel van 40 miskien 6.4, want uit bogenoemde weet ons dat die antwoord waarskynlik effens nader aan 6 as aan 7 is. 
Vermenigvuldig 6,4 met homself, dus 6,4 × 6,4 = 40,96, wat effens groter is as die oorspronklike getal. Dan vermenigvuldig ons die getal met `n tiende kleiner as ons skatting hierbo (omdat ons antwoord te hoog was), en ons kry 6.3 × 6.3 = 39,69. Dit is effens laer as ons oorspronklike getal. Dit beteken dat die vierkantswortel van 40 iewers is tussen 6.3 en 6.4 leuens. Ook, omdat 39.69 nader aan 40 as 40.96 is, weet jy dat die vierkantswortel nader aan 6.3 as aan 6.4 is. 
In ons voorbeeld, kom ons kies 6.33 vir ons raaiskoot in twee desimale plekke. Vierkant 6,33 en jy kry 6,33 × 6,33 = 40,0689. Aangesien dit effens bo ons oorspronklike getal is, sal ons `n effens laer getal probeer, soos 6.32. 6,32 × 6,32 = 39,9424. Dit is effens onder ons oorspronklike getal, so ons weet dat die presiese vierkantswortel tussen 6.33 en 6.32 leuens. As ons verder wou gaan, kan ons voortgaan om dieselfde benadering te gebruik om `n antwoord te kry wat al hoe meer akkuraat is.
Los vierkantswortels op
Inhoud
Terwyl die intimiderende gesig van `n vierkantswortelsimbool mense met wiskunde-angs kan laat ineenkrimp, is vierkantswortelprobleme nie so moeilik om op te los soos dit met die eerste oogopslag lyk nie. Eenvoudige vierkantswortelprobleme kan dikwels net so maklik opgelos word soos eenvoudige vermenigvuldigings- en deelprobleme. Meer komplekse vierkantswortelprobleme, aan die ander kant, kan `n bietjie meer werk verg, maar met die regte benadering kan selfs hierdie probleme maklik opgelos word. Begin vandag om vierkantswortelprobleme te oefen om hierdie wiskundevaardigheid aan te leer wat dalk nuut vir jou is!
Trappe
Deel 1 van 3: Verstaan kragte en wortels

1. Kwadrateer `n getal deur dit met homself te vermenigvuldig. Om wortels te verstaan, is dit die beste om met die vierkante te begin. Kwadrate is maklik - om `n getal te kwadraat is gelykstaande aan om dit met homself te vermenigvuldig. Byvoorbeeld: 3 kwadraat is dieselfde as 3 × 3 = 9, en 9 kwadraat is dieselfde as 9 × 9 = 81. Vierkante word met `n klein "2" bo en regs van die getal gekwadraat aangedui - soos volg: 3, 9, 100, ens.
- Probeer om self `n paar getalle te kwadraat om hierdie konsep te toets. Onthou dat om `n getal te kwadraat niks meer is as om daardie getal met homself te vermenigvuldig nie. Jy kan dit selfs met negatiewe getalle doen. In alle gevalle sal die antwoord altyd positief wees. Byvoorbeeld: -8 = -8 × -8 = 64.

2. Om die wortel van `n getal te vind, vind die `omgekeerde` van `n vierkant. Die simbool van die vierkantswortel (√, ook bekend as die `radikale teken`) is basies die `teenoorgestelde` van die vierkantsimbool (). As jy `n radikale teken sien, kan jy jouself afvra: `Watter getal kan ek met homself vermenigvuldig sodat ek die getal onder die radikale teken kry??` Byvoorbeeld: as jy die vierkantswortel √(9) sien, dan soek jy die getal wat met homself vermenigvuldig het, het nege as die produk. In hierdie geval is dit drie, want 3 = 9.

3. Ken die verskil tussen perfekte en onvolmaakte vierkante. Tot nou toe was die antwoorde op die vierkantswortelprobleme mooi, ronde getalle. Dit is nie altyd die geval nie - in werklikheid is daar antwoorde op vierkantswortels wat baie lang, ongemaklike desimale getalle is. Wortelgetalle wat heelgetalle is (met ander woorde, getalle wat nie breuke of desimale is nie) word genoem vierkante. Al die bogenoemde voorbeelde (9, 25 en 64) is vierkante (ook genoem perfekte vierkante), want deur vierkantswortels te neem, kry ons heelgetalle (3, 5 en 8) as gevolg daarvan.

4. Memoriseer die eerste 10-12 blokkies. Soos jy waarskynlik opgemerk het, is vierkantswortels of vierkante dikwels baie maklik! Omdat hierdie wiskundeprobleme so eenvoudig is, is dit die moeite werd om die wortels van die eerste 12 of meer vierkante te leer. Jy sal hierdie getalle baie teëkom, so jy kan op die lang termyn baie tyd bespaar deur hulle vroeg te leer. Die eerste 12 vierkante is:

5. Vereenvoudig wortels deur vierkante te verwyder waar moontlik. Dit kan soms moeilik wees om die wortels van onvolmaakte vierkante te vind - veral as jy nie `n sakrekenaar gebruik nie (die paragrawe hieronder gee jou truuks om hierdie proses makliker te maak). Dit is egter dikwels moontlik om die getalle onder die radikale teken te vereenvoudig, om dit makliker te maak om daarmee te werk. Om dit te doen, moet jy net die getal onder die radikaal faktoriseer, neem dan die vierkantswortel van faktore wat vierkante is, en skryf die antwoord buite die radikaal. Dit is makliker as wat dit klink - lees verder om meer te wete te kom!

6. Gebruik denkbeeldige getalle vir die wortels van negatiewe getalle. Watter vierkant is -16? Dit is nie 4 of -4 nie - om albei te kwadraat gee 16 (positief). Weet jy nie? Trouens, daar is geen manier om die vierkantswortel van -16 of enige negatiewe getal met gereelde getalle te skryf nie. In hierdie gevalle moet ons denkbeeldige getalle (gewoonlik in die vorm van letters of simbole) gebruik om die vierkantswortel van die negatiewe getal te vervang. Byvoorbeeld, die veranderlike `i` word gewoonlik gebruik vir die vierkantswortel van -1. As `n algemene reël sal die vierkantswortel van `n negatiewe getal altyd `n denkbeeldige getal wees (of een bevat).
Deel 2 van 3: Gebruik langdelingalgoritmes

1. Bestel jou vierkantswortelprobleem soos langdeling. Alhoewel dit `n bietjie tydrowend kan wees, is dit moontlik om die wortels van moeilike onvolmaakte vierkante sonder `n sakrekenaar te bereken. Om dit te doen, gebruik ons `n oplossingsmetode (of algoritme) wat soortgelyk is aan - maar nie presies dieselfde as - `n lang afdeling.
- Skryf eers die vierkantswortel neer op dieselfde manier as langdeling. Byvoorbeeld, kom ons sê ons wil die vierkantswortel van 6,45 bereken, wat beslis nie `n gerieflike perfekte vierkant is nie. Eers skryf ons `n gewone radikale simbool (√), dan skryf ons die getal daaronder. Dan trek ons `n streep bokant die nommer, so dit is in `n klein `boks` — net soos langdeling. Toe ons klaar is, het ons `n langwerpige `√` opgemerk met 6.45 daaronder.
- Ons skryf getalle bo die probleem, so laat `n bietjie spasie.

2. Groepeer die getalle in pare. Om jou probleem op te los, groepeer die syfers van die getal onder die radikale teken in pare, vanaf die desimale punt. Jy kan klein hoogtepunte byvoeg (soos punte, skuinsstreepies, kommas, ens.) tussen jou pare om hulle van mekaar te onderskei.

3. Vind die grootste getal waarvan die vierkant kleiner as of gelyk is aan die eerste `groep`. Begin met die eerste nommer of paar aan die linkerkant. Kies die grootste getal met `n vierkant wat kleiner as of gelyk is aan die `groep`. Byvoorbeeld, as die groep 37 is, sal jy die 6 kies, want 6 = 36 (minder as 37), maar 7 = 49 (meer as 37). Skryf hierdie nommer bo die eerste groep neer. Dit is die eerste syfer van jou antwoord.

4. Verdubbel die getal wat jy sopas neergeskryf het, skryf dit onder die eerste groep en trek dit af. Neem die eerste syfer van jou antwoord (die nommer wat jy sopas gekry het) en verdubbel dit. Skryf dit onder jou eerste groep en trek dit af om die verskil te vind. Plaas die volgende paar getalle langs die antwoord hieronder. Ten slotte, skryf die laaste syfer van dubbel die eerste syfer van jou antwoord aan die linkerkant, en laat `n spasie langs dit.

5. Vul die leë spasie. Vervolgens is die bedoeling om `n syfer regs van die nommer wat jy aan die linkerkant geskryf het by te voeg. Kies `n getal wat vermenigvuldig met jou nuwe getal, lewer die grootste moontlike produk, maar is minder as of gelyk aan die "getekende" getal. Byvoorbeeld, as jou `afgehaal` nommer 1700 is en die getal aan die linkerkant is 40_, sal jy die spasie invul met `404` want 404 × 4 = 1616 (minder as 1700), terwyl 405 × 5 = 2025. Die nommer wat jy in hierdie stap kry, is die tweede syfer van jou antwoord, so jy kan dit bo die radikaal byvoeg.

6. Gaan voort om jou `leë` nommers vir jou antwoord te gebruik. Gaan voort met hierdie gewysigde lang verdeling totdat jy nulle kry wanneer jy die `aftrek`-nommer aftrek, of jy het die verlangde akkuraatheid bereik. Wanneer jy klaar is, is die nommers wat jy gebruik het om die spasies by elke stap te vul (plus die heel eerste nommer wat jy gebruik het) die syfers van jou antwoord.

7. Skuif die desimale punt van jou oorspronklike `deler` op. Om jou antwoord af te rond, moet jy die komma (die desimale punt) op die regte plek plaas. Gelukkig is dit maklik - al wat jy hoef te doen is om dit in lyn te bring met die desimale punt in jou oorspronklike nommer. As die getal onder die radikaal 49,8 is, skuif die desimale punt op tussen die twee getalle bo 9 en 8.
Deel 3 van 3: Skat vinnig onvolmaakte vierkante

1. Vind onvolmaakte vierkante deur te skat. Sodra jy jou vierkante gememoriseer het, word dit baie makliker om die wortels van onvolmaakte vierkante te vind. Aangesien jy reeds `n dosyn vierkante ken, kan enige getal wat tussen twee van hierdie perfekte vierkante val gevind word deur tussen hierdie waardes te skat. Om te begin, vind die twee blokkies wat jou getal tussenin val. Bepaal dan watter van hierdie twee vierkante die naaste aan die getal is.
- Gestel byvoorbeeld ons moet die vierkantswortel van 40 vind. Aangesien ons ons vierkante gememoriseer het, kan ons sê dat 40 tussen 6 en 7 val, of 36 en 49. Aangesien 40 groter as 6 is, sal sy vierkantswortel groter as 6 wees, en aangesien dit minder as 7 is, sal sy vierkantswortel minder as 7 wees. Die getal 40 is `n bietjie nader aan 36 as 49, so die antwoord sal waarskynlik `n bietjie nader aan 6 wees. In die volgende stappe sal ons ons antwoord meer akkuraat maak.

2. Skat die vierkantswortel tot een desimale plek. Sodra jy twee vierkante gekies het waartussen jou nommer lê, is dit net `n kwessie van skat totdat jy `n antwoord kry waarmee jy tevrede is. Hoe verder jy gaan, hoe meer akkuraat is jou antwoord. Om te begin, kies `n tien vir jou antwoord - dit hoef nie korrek te wees nie, maar jy sal tyd bespaar as jy gesonde verstand gebruik deur `n nommer te kies wat naby die korrekte antwoord is.

3. Vermenigvuldig die skatting op sigself. Dan vier jy die skatting. Tensy jy gelukkig is, sal jy waarskynlik nie jou oorspronklike nommer kry nie - jy sal óf effens hoër óf laer eindig. As jou antwoord te hoog is, probeer weer met `n effens kleiner skatting (en omgekeerd as dit te laag is).

4. Gaan voort om te skat indien nodig. As jy tevrede is met jou antwoorde, wil jy dalk net een van jou eerste raaiskote gebruik. As jy egter `n meer akkurate antwoord wil hê, is al wat jy hoef te doen om `n skatting vir jou "honderdste" te kies wat hierdie skatting tussen jou eerste twee plaas. As jy met hierdie patroon voortgaan, kan jy `n antwoord in drie, vier of meer desimale plekke kry - dit hang net af van hoe ver jy wil gaan.
Wenke
- Vir vinnige oplossings, gebruik `n sakrekenaar. Die meeste moderne sakrekenaars kan vierkantswortels direk bereken. Gewoonlik hoef jy net jou nommer in te voer en dan die knoppie met die radikaal van die tweede mag (die vierkantswortel) te druk. Byvoorbeeld, om die vierkantswortel van 841 te vind, druk die volgende sleutels: 8, 4, 1, (√) en kry dit reg 29 op as antwoord.
Artikels oor die onderwerp "Los vierkantswortels op"
Оцените, пожалуйста статью
Gewilde