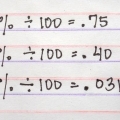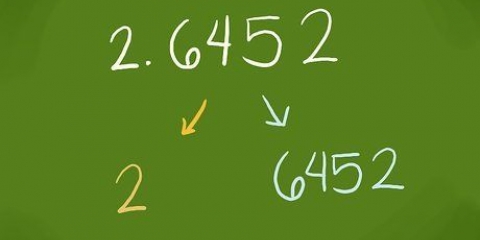Byvoorbeeld, in breuke hang die grootte van die `helfte` van iets af van die totale aantal stukke. As jou `pastei` in agt stukke verdeel word, sal die helfte daarvan -- vier wees. Maar as jou `pastei` in 22 stukke verdeel is, dan is die helfte 11. Die doelwit sal altyd verander. Maar met persentasies is die helfte altyd dieselfde -- 50%. 
Gestel jy het byvoorbeeld die breuk 1/2. Op jou sakrekenaar doen jy die bewerking 1 2, en die sakrekenaar wys die resultaat 0.5. Nog `n voorbeeld, skakel die breuk 1/4 om na `n desimale deur die bewerking 1 ÷ 4 te gebruik. Die resultaat is 0,25. Vir `n meer komplekse voorbeeld, kan jy die breuk 274/312 omskakel na `n desimale met die bewerking 274 ÷ 312. Die resultaat sal 0,878 wees. (Daar is meer syfers na die desimale punt, maar drie is genoeg vir hierdie doel). 
Neem die bostaande voorbeeld van 1/2, wat ons omgeskakel het na die desimale 0,5. Om hierdie desimale as `n persentasie te vertoon, skuif die desimale twee plekke na regs. Eerstens herskryf jy 0.5 as 0.50. Dan skuif jy die desimale punt twee plekke na regs en 0.50 word die persentasie 50%. Die voorbeeld 1/4, met die ekwivalente desimale punt 0.25, kan omgeskakel word na die persentasie 25%. 
3/4=75% 1/2=50% 1/3=33 1/3% 1/4=25% 1/5=20% 1/8=12.5% (dikwels gebruik in bankwese) 

Gestel jy wil byvoorbeeld `n inkomstepersentasie bereken. 100% veronderstel die volle inkomste vir `n projek, maar jy moet 10% aftrek vir uitgawes, 12% vir salarisse en 25% vir belasting. Hoeveel is daar oor? Gebruik jou sakrekenaar om hierdie aftrekking uit te voer (100-10-12-25). Die resultaat is 53%. 
Die laaste uitslag mag dalk verbasend lyk as jy verwag dat `n verdeling `n kleiner resultaat as die beginnommer sal oplewer. Jy moet egter verstaan dat deling deur `n getal minder as een altyd die wederkerigheid van daardie getal sal verhoog. Byvoorbeeld, om deur 1/10 te deel is dieselfde as om met 10 te vermenigvuldig. Om deur 1/2 te deel is dieselfde as om met 2 te vermenigvuldig. 

Byvoorbeeld, in die oefening 15% van 100, herskryf 15% as 0.15. Dan vermenigvuldig jy 0,15 x 100, en die oplossing is 15. 
In die voorbeeld 15% van 100 is die resultaat die heelgetal 15. 

Byvoorbeeld, om 4% op jou sakrekenaar om te skakel, druk die 4 en dan %. Jou sakrekenaar sal die 4 omskakel na 0,04, die desimale ekwivalent. Om 82,5% na `n desimale om te skakel, voer 8, 2 in, . , 5, %. Die sakrekenaar wys dan die getal 0,825. 
Wanneer jy `n sakrekenaar gebruik om persentasies te bereken, druk die Clear (C) of All Clear (AC) sleutels voordat jy begin. Wanneer jy die getalle vir hierdie berekening insleutel, moet jy in gedagte hou dat sodra jy die %-sleutel druk, die getal 15 omgeskakel sal word na 0.15. Die sakrekenaar sal voortgaan om 0,15 x 75,32 te bereken.
Berekening van persentasies op 'n sakrekenaar
Inhoud
`n Persentasie is `n spesiale manier om `n deel van iets te wys. `n Persentasie is `n getal wat `n breuk aandui, verdeel in 100 stukke. Dus, 100% is die geheel (dit wat gemeet word), terwyl 50% die helfte van daardie getal is. Deur te leer om getalle as persentasies te skryf, maak dit makliker om vermenigvuldiging en ander berekeninge op `n sakrekenaar te doen. Sommige sakrekenaars het selfs `n %-knoppie wat die berekening nog makliker maak.
Trappe
Metode 1 van 4: Skakel breuke en desimale om na persentasies

1. Leer die algemene betekenis van breuke. `n Breuk is `n vergelyking van twee getalle, wat gewoonlik die grootte van `n deel in verhouding tot die geheel aandui. `n Klassieke voorbeeld is `n pastei wat in agt gelyke stukke verdeel word. Die boonste getal van die breuk word die teller genoem, en dit verteenwoordig die aantal stukke wat jy gekies het. Die onderste getal word die noemer genoem, en verteenwoordig die totale aantal stukke van die pastei -- in hierdie geval, 8.
- Byvoorbeeld, die breuk 1/8 is een stuk van die tert uit agt stukke in totaal.
- Die breuk 7/8 dui 7 stukke aan, amper die hele tert.

2. Herken die spesiale verhouding van persentasies. `n Persentasie is `n spesiale soort breuk, waar die noemer altyd 100 is. Alhoewel dit nie prakties is wanneer jy `n pastei sny nie, is die konsep van persentasies baie nuttiger omdat dit standaard is.

3. Gebruik `n sakrekenaar om `n breuk na `n desimale of persentasie om te skakel. As jy met `n breuk aangebied word, kan jy dit maklik met `n sakrekenaar na `n desimale getal omskakel. Hou net in gedagte dat `n breuk `n deelprobleem is, en gebruik jou sakrekenaar om die teller deur die noemer te deel. Jou sakrekenaar sal vir jou die desimale ekwivalent van die breuk gee.

4. Skakel desimale getalle om na persentasies deur die desimale punt te skuif. As die getal reeds `n desimale is, kan jy dit maklik omskakel na `n persentasie. Aangesien die desimale getallestelsel op die basis 10 gebaseer is, kan jy `n desimale na `n persentasie omskakel deur die desimale twee plekke na regs te skuif en dan `n %-teken daarna by te voeg. As jou desimale net een desimale plek het, kan jy nulle aan die regterkant van die getal byvoeg en 0,5 na 0,50 of selfs 0,500 omskakel. Dit het almal dieselfde numeriese waarde.

5. Memoriseer die standaard omskakelings. Dit is nuttig as jy die persentasies van sekere standaardbreuke ken. Omdat die noemer van `n persentasie altyd 100 is, bly sekere waardes konstant. Byvoorbeeld, jy moet die volgende omskakelings ken:
Metode 2 van 4: Doen basiese berekeninge met persentasies

1. Voeg persentasies direk saam. Omdat persentasies basies alle breuke met `n noemer van 100 is, kan jy `n lys van persentasies maak wat jy nie hoef om te skakel nie. In teenstelling hiermee, onthou dat die byvoeging van breuke vereis dat jy deur die stappe gaan om die gemene deler te vind en jou breuke om te skakel na daardie gemene delers. Met persentasies is daar egter geen ekstra werk nodig nie. Jy kan net die persentasies bymekaar tel.
- Byvoorbeeld, as ses mense `n deel kry van die totale lone wat binne `n maatskappy betaal word, kan jy bepaal hoeveel hulle saam verteenwoordig deur die relatiewe persentasies by te tel. As hulle onderskeie aandele 10%, 5%, 8%, 22%, 10% en 8% is, dan kan jy dit net bymekaartel, en so 10+5+8+22+10+8=63. Hierdie ses mense verdien saam 63% van die lone wat die maatskappy betaal.
- Wanneer jy byvoeg, ignoreer die persentasie simbool, en voeg net die getalle by. Plaas die simbool weer agter die finale antwoord.

2. Trek persentasies op dieselfde manier af. Weereens, omdat persentasies breuke met `n noemer van 100 verteenwoordig, hoef jy geen bykomende werk te doen om persentasies af te trek nie. As jy `n persentasie van `n geheel wil aftrek, verteenwoordig jy daardie geheel met die getal 100 (want die geheel is 100%).

3. Vermenigvuldig of deel met behulp van desimale ekwivalente. As jy `n probleem het wat oorspronklik as 25% x 30 geskryf is, skryf die 25% as sy desimale ekwivalent 0.25 en voer die bewerking uit. Dit word dan 0,25 x 30 wat lei tot 7,5. Net so, as jy `n deelprobleem van 200 10% het, skryf dit oor as 200 ÷ 0.10 en voer dit in jou sakrekenaar in. Die resultaat sal 2000 wees.
Metode 3 van 4: Bereken `n persentasie van `n heelgetal

1. Vermenigvuldig om die persentasie `van` `n getal te vind. `n Algemene berekening met persentasies is om die persentasie `van` `n ander getal te bepaal. Byvoorbeeld, as jy in `n restaurant is, wil jy dalk 15% `van` jou totale rekening `n fooi gee. Wanneer met persentasies gewerk word, het die woord `van` dieselfde betekenis as `tye` of `vermenigvuldig`. Daarom, byvoorbeeld, beteken 15% `van` 100 dieselfde as 15/100 x 100.

2. Skakel die persentasie om na `n desimale en vermenigvuldig. Om die persentasie van `n heelgetal te bereken, moet jy eers die persentasie omskakel na `n desimale getal, soos vroeër beskryf. Dan kan jy net vermenigvuldig.

3. Teken jou resultaat aan sonder `n persentasie simbool. Wanneer jy die persentasie van `n heelgetal wil bepaal, is jou resultaat `n getal en nie `n persentasie nie. Jy kan begin deur `n persentasie simbool aan te teken, maar wanneer jy daardie persentasie na `n desimale getal omskakel, doen jy die vermenigvuldiging en jou antwoord sal nie meer `n persentasie simbool kry nie.
Metode 4 van 4: Gebruik die %-sleutel op `n sakrekenaar

1. Vind die %-sleutel op jou sakrekenaar. Die meeste basiese sakrekenaars het wel `n sleutel met `n %-simbool. Meer gevorderde grafiese sakrekenaars het dalk nie hierdie sleutel nie, aangesien die vervaardigers verwag dat jy hierdie bewerkings sonder `n spesiale sleutel sal kan uitvoer. Maar baie standaard sakrekenaars het hierdie sleutel.

2. Eksperimenteer met die %-sleutel vir desimale omskakelings. Die maklikste manier om die %-sleutel te gebruik, is om `n getal van persentasie na desimale vorm om te skakel. Tik die getal in en druk die %-sleutel, dan sal die sakrekenaar die desimale ekwivalent wys.

3. Gebruik die %-sleutel vir berekeninge. Die %-sleutel op jou sakrekenaar maak sekere berekeninge baie maklik. Gestel jy wil `n fooitjie bereken, en jy het vasgestel dat 15% van die totale rekening 75,32 is. As jy `n sakrekenaar byderhand het, voer 15% x 75,32 in. Die resultaat behoort dan 11,298 te wees, `n fooi van €11,30.
Benodigdhede
- Sakrekenaar
- Potlood
- Papier
Artikels oor die onderwerp "Berekening van persentasies op 'n sakrekenaar"
Оцените, пожалуйста статью
Soortgelyk
Gewilde