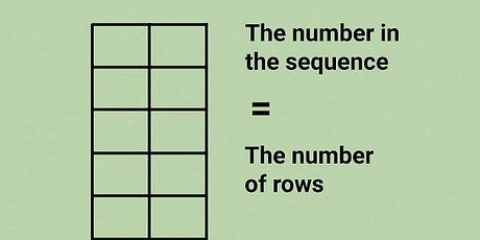
In hierdie voorbeeld is die eerste stel van drie getalle vermenigvuldig gelyk aan 10. Bepaal die grootste kubus wat minder as 10 is. Dit is 8, en sy derdemagswortel is 2. Skryf die nommer 2 bo die radikale teken, bo die nommer 10. Skryf die waarde van neer  , gelyk aan 8, onder die getal 10; trek `n lyn en trek die getalle af op dieselfde manier as in langdeling. Die resultaat is 2.
, gelyk aan 8, onder die getal 10; trek `n lyn en trek die getalle af op dieselfde manier as in langdeling. Die resultaat is 2. Na hierdie minussom het jy die eerste syfer van jou antwoord. Jy sal moet kyk of hierdie een nommer presies genoeg is. In die meeste gevalle sal dit nie die geval wees nie. Jy kan dit nagaan deur die nommer na die kubus te verhoog en te kyk of dit naby genoeg aan die verlangde resultaat is. In hierdie geval  is gelyk aan 8, en dit is nie regtig naby aan 10 nie, so jy moet aanbeweeg.
is gelyk aan 8, en dit is nie regtig naby aan 10 nie, so jy moet aanbeweeg. 
Skryf aan die linkerkant van die vertikale lyn die oplossing van die volgende deler neer, as die som van drie afsonderlike getalle. Dui die leë spasies vir hierdie nommers aan deur drie leë spasies met plustekens onder hulle te onderstreep. 


Bereken nou 3 keer 10 keer elk van die twee getalle wat in jou oplossing bo die radikaal bestaan. Vir hierdie eenvoudige probleem beteken dit 3*10*2*1, wat gelyk is aan 60. Voeg dit by die 1200 wat jy reeds gehad het en jy kry 1260. Voeg laastens die vierkant van die laaste syfer by. In hierdie voorbeeld is dit 1; en 1^2 is steeds 1. Die totale deler is dus 1200+60+1, of 1261. Let op dit aan die linkerkant van die vertikale lyn. 

Jy kan die akkuraatheid van hierdie resultaat nagaan deur die kubus te gebruik: 2.1*2.1*2.1. Die resultaat is 9 261. As jy dink die resultaat is presies genoeg, kan jy stop. As jy ’n meer presiese antwoord wil hê, moet jy deur nog ’n rondte gaan. 
Neem die volgende groep van drie getalle af. In hierdie geval is dit drie nulle, wat na die res 739 en dus 739 kom.000 vorms. Begin die deler by 300 keer die kwadraat van die getal tans bokant die radikaal. Dit is  , en dus 132.300.
, en dus 132.300. Kies die volgende syfer van jou oplossing sodat jy dit met 132 kan vermenigvuldig.300 en minder van die 739.000 van jou res. `n Goeie keuse sal 5 wees, want 5*132.300=661.500. Skryf die getal 5 in die volgende spasie bokant die radikale lyn. Soek 3 keer die vorige getal bokant die radikale lyn, 21, maal die laaste syfer wat jy sopas neergeskryf het, 5, maal 10. Dit gee  .
. Laastens vier jy die laaste syfer. Dit is 
Tel jou deler se terme bymekaar en jy kry 132.300+3150+25=135.475. 
Vermenigvuldig die deler met die laaste syfer van jou oplossing. 135.475*5=677.375. aftrek. 739.000-677.375=61.625. Oorweeg of die oplossing 2.15 presies genoeg is. Bereken sy kubus en jy kry  .
. 


In die voorbeeldprobleem val 600 (jou teikengetal) omtrent halfpad tussen die limietgetalle 512 en 729. Kies dus jou 5 as jou volgende nommer. 
In hierdie voorbeeld vermenigvuldig jy 

Byvoorbeeld, in hierdie probleem,  groter as teiken (600). Dus verminder jy die skatting na 8,4. Neem die kubus van hierdie nommer en vergelyk dit met jou teiken. jy sal dit sien
groter as teiken (600). Dus verminder jy die skatting na 8,4. Neem die kubus van hierdie nommer en vergelyk dit met jou teiken. jy sal dit sien  . Dit is nou laer as jou teiken. Dit sê vir jou dat die derdemagswortel van 600 ten minste 8,4 moet wees, maar minder as 8,5.
. Dit is nou laer as jou teiken. Dit sê vir jou dat die derdemagswortel van 600 ten minste 8,4 moet wees, maar minder as 8,5. 
In hierdie voorbeeldprobleem wys jou laaste rondte berekeninge dit  , terwyl
, terwyl  . Die teiken (600) is effens nader aan 592 as aan 614. Skat jy dus die volgende getal bietjie minder as halfpad tussen 0 en 9. `n Goeie keuse is 4, wat jou `n skatting van die derdemagswortel van 8,44 sal gee.
. Die teiken (600) is effens nader aan 592 as aan 614. Skat jy dus die volgende getal bietjie minder as halfpad tussen 0 en 9. `n Goeie keuse is 4, wat jou `n skatting van die derdemagswortel van 8,44 sal gee. 
Vir hierdie voorbeeldprobleem, begin deur dit op te let  . Dit is net bokant die teiken, so laat val `n paar en toets 8.43. Dit gee
. Dit is net bokant die teiken, so laat val `n paar en toets 8.43. Dit gee  as gevolg. So jy weet dat die derdemagswortel van 600 `n bietjie meer as 8,43 en `n bietjie minder as 8,44 is.
as gevolg. So jy weet dat die derdemagswortel van 600 `n bietjie meer as 8,43 en `n bietjie minder as 8,44 is. 
Vir die voorbeeld van die derdemagswortel van 600, met die aanname van twee desimale getalle, is 8,43 minder as 1 weg van die teikengetal. As jy voortgaan tot drie syfers na die desimale punt, sal jy dit sien  as die resultaat 0,1 minder is as die werklike antwoord.
as die resultaat 0,1 minder is as die werklike antwoord. 

Om meer te wete te kom oor Newton se binomiaal en hierdie resultaat te kry, lees meer oor die vermenigvuldiging van binomiale op wikiHow. As jy `n meer in-diepte, vinnige weergawe wil hê, lees meer oor Pascal se Driehoek. 

Die eerste term bevat `n meervoud van 1000. Jy kies eers `n getal wat tot die kubus verhoog kan word en steeds binne die reeks van langdeling bly as die eerste syfer. Dit lewer die term 1000A^3 in die binomiaal. Die tweede term van Newton se binomiaal het `n koëffisiënt van 300. (Dit is van  .) Onthou dat wanneer die derdemagswortel bereken word, die eerste syfer in elke stap vermenigvuldig is met 0300.
.) Onthou dat wanneer die derdemagswortel bereken word, die eerste syfer in elke stap vermenigvuldig is met 0300. Die tweede syfer in elke stap van die derdemagswortelberekening kom van die derde term van Newton se binomiaal. In Newton se binomiaal sien jy die term 30AB^2. Die laaste syfer van elke stap is die term B^3. 
Berekening van kubuswortels met die hand
Inhoud
Deur `n sakrekenaar te gebruik, om die derdemagswortel van enige getal te bereken, druk net `n paar sleutels. Maar miskien het jy nie `n sakrekenaar nie of wil jy jou vriende beïndruk met jou vermoë om `n derdemagswortel vanself te bereken. Daar is `n metode wat met die eerste oogopslag `n bietjie taai lyk, maar met `n bietjie oefening baie maklik werk. Dit is nuttig om `n bietjie gereed kennis te hê op die gebied van rekenkundige vaardighede en die berekening van kubieke getalle.
Trappe
Deel 1 van 3: Werk `n voorbeeldopdrag uit

1. Berei die opdrag voor. Om die derdemagswortel van `n getal op te los, sal lyk soos die oplossing van langdeling, met `n paar verskille hier en daar. Die eerste stap is om die probleem korrek neer te skryf.
- Skryf die getal neer waarvan jy die derdemagswortel wil vind. Skryf die getalle in groepe van drie, waar die komma die beginpunt is. In hierdie voorbeeld gaan jy die derdemagswortel van 10 vind. Skryf dit neer as 10,000000. Die nulle is nodig vir die akkuraatheid van die antwoord.
- Trek `n radikaal van die kubus oor die getal. Dit dien dieselfde doel as die lang verdelingslyn. Die enigste verskil is die vorm van die simbool.
- Plaas `n komma bo die lyn, direk bo die desimale punt in die oorspronklike getal.

2. Ken die kubusse van die eenhede. Jy sal dit in jou berekeninge gebruik. Dit gaan oor die volgende derde magte:











3. Vind die eerste syfer van jou antwoord. Kies `n getal wat, vir die kubus, die grootste moontlike uitkoms gee wat minder is as die eerste stel van drie getalle.
 , gelyk aan 8, onder die getal 10; trek `n lyn en trek die getalle af op dieselfde manier as in langdeling. Die resultaat is 2.
, gelyk aan 8, onder die getal 10; trek `n lyn en trek die getalle af op dieselfde manier as in langdeling. Die resultaat is 2. is gelyk aan 8, en dit is nie regtig naby aan 10 nie, so jy moet aanbeweeg.
is gelyk aan 8, en dit is nie regtig naby aan 10 nie, so jy moet aanbeweeg.
4. Maak die opstelling vir die volgende syfer. Skryf die volgende groep van drie getalle in die res, en trek `n kort vertikale lyn aan die linkerkant van die resulterende getal. Dit sal die getal wees wat ons gebruik om die volgende syfer in jou derdemagsworteloplossing te bepaal. In hierdie voorbeeld sal dit 2000 wees, wat geskep word uit die res 2 van die vorige minus som, met die groep van drie nulle wat jy afgeneem het.

5. Vind die begin van die volgende deler. Skryf vir die eerste deel van die deler driehonderd keer die kwadraat van wat ook al bo die radikaal is. In hierdie geval is dit 2; 2^2 is 4, en 4*300=1200. Skryf dus 1200 in die eerste leë spasie. Die deler vir hierdie stap van die oplossing gaan 1200 wees, plus iets anders wat jy binne `n minuut sal bereken.

6. Vind die volgende getal in jou derdemagswortel. Vind die volgende syfer van jou oplossing deur te kies wat jy kan vermenigvuldig met die deler (1200-en-iets), trek dan af van die res van 2000. Dit kan net 1 wees, want 2 keer 1200 is gelyk aan 2400, wat groter is as 2000. Skryf die nommer 1 in die volgende spasie bokant die radikaal.

7. Vind die res van die deler. Die deler in hierdie stap van die oplossing bestaan uit drie dele. Die eerste deel is die 1200 wat jy reeds het. Jy sal nou twee ekstra terme moet byvoeg om die deler te voltooi.

8. Vermenigvuldig en trek af. Rond hierdie deel van die oplossing af deur die laaste syfer van jou oplossing te vermenigvuldig - in hierdie geval die getal 1 - keer die deler wat jy pas bereken het (1261). 1*1261 =1261. Skryf dit hieronder 2000 en trek 1261 daarvan af om 739 te kry.

9. Besluit jy moet verder gaan vir `n meer akkurate antwoord. Nadat jy die minussom van elke stap voltooi het, moet jy kyk of jou antwoord presies genoeg is. Vir die derdemagswortel van 10: na die eerste minussom was die derdemagswortel net 2, en dit is nie regtig presies nie. Nou, na die tweede rondte, is die oplossing 2.1.

10. Bepaal die handelaar vir die volgende rondte. In hierdie geval, vir meer oefening en `n meer presiese antwoord, herhaal die stappe vir nog `n rondte, soos volg:
 , en dus 132.300.
, en dus 132.300. .
.

11. Vermenigvuldig die deler met die resultaat. Nadat u die deler in hierdie volgende rondte bereken het en u oplossing met nog een syfer uitgebrei het, gaan soos volg voort:
 .
.
12. Skryf jou finale antwoord neer. Die resultaat bokant die radikaal is die derdemagswortel, met `n akkuraatheid van drie beduidende syfers. In hierdie voorbeeld is die derdemagswortel van 10 gelyk aan 2,15. Kontroleer dit deur 2.15^3=9.94 te bereken wat na bo afgerond kan word na 10. As jy `n meer akkurate antwoord nodig het, hou aan totdat jy tevrede is.
Deel 2 van 3: Vind die derdemagswortel deur herhaalde skatting

1. Gebruik kubieke getalle om die boonste en onderste grense te stel. Wanneer jy gevra word vir `n derdemagswortel van `n sekere getal, begin deur `n derdemag te kies wat so na as moontlik daaraan is, sonder om groter as jou teikengetal te wees.
- Byvoorbeeld, as jy die derdemagswortel van 600 wil vind, onthou (of gebruik `n tabel van derdemagte) dat
en
. Daarom sal die oplossing vir die derdemagswortel van 600 iets tussen 8 en 9 wees. Gebruik die nommers 512 en 729 as boonste en onderste grense vir jou oplossing.

2. Raai die volgende nommer. Jy het die eerste syfer geken vanweë jou kennis van sekere kubieke getalle. Vir die volgende syfer, skat `n getal tussen 0 en 9 gebaseer op waar jou teikengetal tussen die twee grensgetalle val.

3. Toets jou raaiskoot deur sy kubus te bepaal. Probeer die skatting waarmee jy nou werk vermenigvuldig om te sien hoe naby jy aan die teikengetal is.


4. Pas jou skatting aan waar nodig. Nadat u tot die kubus van u laaste raai gekom het, kyk na die resultaat teenoor u teikengetal. As die resultaat groter is as die teiken, moet jou skatting kleiner wees. As die resultaat minder as die doelwit is, moet jy dit opwaarts aanpas totdat jy die doelwit bereik.
 groter as teiken (600). Dus verminder jy die skatting na 8,4. Neem die kubus van hierdie nommer en vergelyk dit met jou teiken. jy sal dit sien
groter as teiken (600). Dus verminder jy die skatting na 8,4. Neem die kubus van hierdie nommer en vergelyk dit met jou teiken. jy sal dit sien  . Dit is nou laer as jou teiken. Dit sê vir jou dat die derdemagswortel van 600 ten minste 8,4 moet wees, maar minder as 8,5.
. Dit is nou laer as jou teiken. Dit sê vir jou dat die derdemagswortel van 600 ten minste 8,4 moet wees, maar minder as 8,5.
5. Skat die volgende getal vir `n meer akkurate antwoord. Gaan voort met hierdie prosedure om getalle van 0 tot 9 te skat totdat jou antwoord so akkuraat is as wat jy wil hê dit moet wees. Vir elke skattingsronde, begin deur die posisie van jou laaste berekening tussen die grensgetalle na te gaan.
 , terwyl
, terwyl  . Die teiken (600) is effens nader aan 592 as aan 614. Skat jy dus die volgende getal bietjie minder as halfpad tussen 0 en 9. `n Goeie keuse is 4, wat jou `n skatting van die derdemagswortel van 8,44 sal gee.
. Die teiken (600) is effens nader aan 592 as aan 614. Skat jy dus die volgende getal bietjie minder as halfpad tussen 0 en 9. `n Goeie keuse is 4, wat jou `n skatting van die derdemagswortel van 8,44 sal gee.
6. Gaan voort om te skat en aan te pas Doen dit soveel keer as wat nodig is, verhoog jou skatting na die kubus en kyk hoe dit met die teikengetal vergelyk. Soek getalle wat net onder of net bokant die teikengetal is.
 . Dit is net bokant die teiken, so laat val `n paar en toets 8.43. Dit gee
. Dit is net bokant die teiken, so laat val `n paar en toets 8.43. Dit gee  as gevolg. So jy weet dat die derdemagswortel van 600 `n bietjie meer as 8,43 en `n bietjie minder as 8,44 is.
as gevolg. So jy weet dat die derdemagswortel van 600 `n bietjie meer as 8,43 en `n bietjie minder as 8,44 is.
7. Gaan voort totdat jy die verlangde akkuraatheid bereik. Gaan voort om te skat, te vergelyk en te herskat, so lank as wat nodig is, totdat jou oplossing so akkuraat is as wat jy wil hê dit moet wees. Let daarop dat met elke desimale, jou teikengetalle nader en nader aan die werklike getal kom.
 as die resultaat 0,1 minder is as die werklike antwoord.
as die resultaat 0,1 minder is as die werklike antwoord.Deel 3 van 3: Verstaan hoe hierdie berekening werk

1. Gaan weer oor Newton se binomiaal. Om te verstaan hoekom hierdie algoritme werk vir die bepaling van derdemagswortels, moet jy eers terugdink aan hoe die kubus as binomiaal lyk. Jy het dit waarskynlik in hoërskoolwiskunde geleer (en soos die meeste mense het jy dit waarskynlik redelik vinnig vergeet). Kies twee veranderlikes  en
en  vir die verteenwoordiging van eenhede. Dan bereken jy die binomiaal van
vir die verteenwoordiging van eenhede. Dan bereken jy die binomiaal van  vir die tiene.
vir die tiene.
 en
en  vir die verteenwoordiging van eenhede. Dan bereken jy die binomiaal van
vir die verteenwoordiging van eenhede. Dan bereken jy die binomiaal van  vir die tiene.
vir die tiene. - Gebruik die term
om `n dosyn te skep. Vir watter graad jy ook al kies
,
sal `n dosyn vorm. Byvoorbeeld, as
is 2 en
6 is, word dan
gelyk aan 26.

2. Skryf die binomiaal in `n kubus. Ons werk nou agteruit, deur eers die kubus te bepaal en dan te sien hoekom die kubusworteloplossing werk. Ons benodig die waardes van  vind. Jy doen dit deur te oefen
vind. Jy doen dit deur te oefen  . Dit is `n te lang berekening om hier te wys, maar die eindresultaat is
. Dit is `n te lang berekening om hier te wys, maar die eindresultaat is  .
.
 vind. Jy doen dit deur te oefen
vind. Jy doen dit deur te oefen  . Dit is `n te lang berekening om hier te wys, maar die eindresultaat is
. Dit is `n te lang berekening om hier te wys, maar die eindresultaat is  .
.
3. Ken die betekenis van lang verdeling. Let daarop dat die metode vir die berekening van die derdemagswortel net soos langdeling werk. In langdeling sien jy dat twee faktore saam vermenigvuldig, gee die getal waarmee jy begin het. In hierdie berekening is die getal waarna jy soek (die getal wat bo die radikaal eindig) die derdemagswortel. Dit beteken dit is gelyk aan die term (10A+B). Die werklike A en B is nou irrelevant, solank jy die verband met die antwoord verstaan.

4. Kyk na die uitgebreide weergawe. As jy na Newton se binomiaal kyk, sien jy hoekom die derdemagswortelalgoritme korrek is. Kyk hoe die deler by elke stap van die algoritme gelyk is aan die som van die vier terme wat jy nodig het om te bereken en bymekaar te tel. Hierdie terme ontstaan soos volg:
 .) Onthou dat wanneer die derdemagswortel bereken word, die eerste syfer in elke stap vermenigvuldig is met 0300.
.) Onthou dat wanneer die derdemagswortel bereken word, die eerste syfer in elke stap vermenigvuldig is met 0300.
5. Kyk na akkuraatheid groei. Deur langverdeling uit te werk, gee elke stap wat jy voltooi groot akkuraatheid aan jou antwoord. Byvoorbeeld, die voorbeeldprobleem wat in hierdie artikel uitgebrei word, is vir die bepaling van die derdemagswortel van 10. In die eerste stap is die oplossing 2, want  kom naby, maar is minder as 10. In werklikheid,
kom naby, maar is minder as 10. In werklikheid,  . Na die tweede rondte is jou oplossing 2.1. Sodra jy dit uitgewerk het, sal jy kry
. Na die tweede rondte is jou oplossing 2.1. Sodra jy dit uitgewerk het, sal jy kry , en dit is baie nader aan die gewenste resultaat (10). Na die derde rondte het jy 2.15, en dit gee jou
, en dit is baie nader aan die gewenste resultaat (10). Na die derde rondte het jy 2.15, en dit gee jou  . Hou aan om in groepe van drie getalle te werk en jy sal so akkuraat `n antwoord kry as wat jy wil.
. Hou aan om in groepe van drie getalle te werk en jy sal so akkuraat `n antwoord kry as wat jy wil.
 kom naby, maar is minder as 10. In werklikheid,
kom naby, maar is minder as 10. In werklikheid,  . Na die tweede rondte is jou oplossing 2.1. Sodra jy dit uitgewerk het, sal jy kry
. Na die tweede rondte is jou oplossing 2.1. Sodra jy dit uitgewerk het, sal jy kry , en dit is baie nader aan die gewenste resultaat (10). Na die derde rondte het jy 2.15, en dit gee jou
, en dit is baie nader aan die gewenste resultaat (10). Na die derde rondte het jy 2.15, en dit gee jou  . Hou aan om in groepe van drie getalle te werk en jy sal so akkuraat `n antwoord kry as wat jy wil.
. Hou aan om in groepe van drie getalle te werk en jy sal so akkuraat `n antwoord kry as wat jy wil.Wenke
- Soos enigiets, sal jou wiskunde vaardighede verbeter met oefening. Hoe meer jy oefen, hoe beter sal jy hierdie soort berekeninge kan doen.
Waarskuwings
- Dit is maklik om `n fout hier te maak. Gaan jou werk noukeurig na en gaan weer deur die uitwerking.
Benodigdhede
- Pen of potlood
- Papier
- Heerser
- Uitveër
Artikels oor die onderwerp "Berekening van kubuswortels met die hand"
Оцените, пожалуйста статью
Soortgelyk
Gewilde