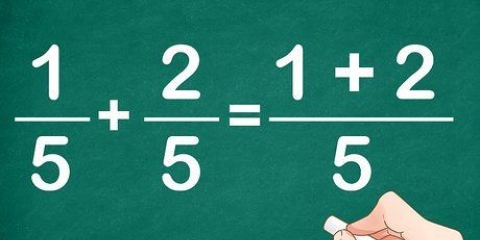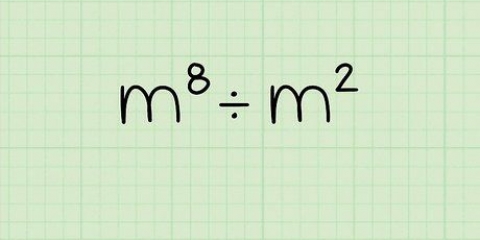Voorbeeld: die volgende uitdrukking 2x + 4(5 + 2) + 3 - (3 + 4/2). Los eers die terme tussen hakies op, dus 5 + 2 en 3 + 4/2. 5 + 2 = 7. 3 + 4/2 = 3 + 2 = 5. Die term tussen die tweede paar hakies word 5 want ons moet eers 4/2 bereken en dan eers die optelling uitwerk. As ons bloot van links na regs sal werk, dan sal die som 3 + 4 : 2 wees, waardeur eers 3 + 4 en dan 7 / 2 bereken sal word, wat lei tot die verkeerde antwoord 7/2. Let wel – as veelvuldige hakies geneste is (hakies binne hakies), los eers die binneste een op en werk na die buitenste hakies. 
Nadat die hakies opgelos is, het die voorbeeld so gelyk. 2x + 4(7) + 3 - 5. Die enigste krag in ons voorbeeld is 3, en dit is gelyk aan 9. Die uitdrukking word nou 2x + 4(7) + 9 - 5. 
Daar is twee vermenigvuldigings in die probleem: 2x (2x is 2 × x) en 4(7). Ons ken nie die waarde van x nie, so kom ons laat dit as 2x. 4(7) = 4 × 7 = 28. Ons kan dit anders skryf as 2x + 28 + 9 - 5. 
Aangesien ons reeds `n delingsprobleem opgelos het wat tussen hakies was, is daar geen delingsprobleme in ons probleem oor nie, so ons kan hierdie stap oorslaan. Dit bring `n belangrike punt na vore - as `n bewerking nie in `n uitdrukking voorkom nie, gaan dan voort na die volgende bewerking soos aangedui in die wiskundereëls. 
Ons uitdrukking is nou gedeeltelik vereenvoudig tot "2x + 28 + 9 - 5". Nou tel ons soveel as moontlik bymekaar – van links na regs. Ons kan nie 2x by die ander getalle tel nie, want ons ken nie die waarde van x nie, so ons slaan hierdie een oor. 28 + 9 = 37, sodat ons die uitdrukking kan herskryf as "2x + 37 - 5". 
In ons uitdrukking, "2x + 37 - 5", daar is net een aftrekking,37 - 5 = 32 
Ons finale antwoord is "2x + 32". Ons kan nie die optelling oplos sonder om die waarde van x te ken nie, maar sodra ons dit doen, is dit baie makliker om op te los as die oorspronklike uitdrukking. 

Gestel byvoorbeeld ons moet die breuk 36/60 oplos. As ons `n sakrekenaar byderhand het, word die antwoord (6) so bereken. As ons dit nie het nie, kan ons `n lang pad gaan deur soortgelyke faktore uit te skakel. Nog `n manier om oor 36/60 te dink, is as (6 × 6)/(6 × 10). Dit kan weer as 6/6 × 6/10 herskryf word. 6/6 = 1, dus word ons uitdrukking 1 × 6/10 = 6/10. Maar ons is nog nie daar nie – beide 6 en 10 het dieselfde faktor van 2. Deur die bogenoemde prosedure te herhaal, hou ons3/5 oor. 
Gestel ons het die uitdrukking (3x + 3x)/(-3x + 15x).Hierdie breuk kan herskryf word as (x + 1)(3x)/(3x)(5 - x), 3x kom in beide die teller en die noemer voor. Die verwydering van hierdie faktore uit die vergelyking gee (x + 1)/(5 - x). Net so is dit die geval met die vergelyking (2x + 4x + 6)/2. Aangesien elke term deelbaar is deur 2, kan ons dit herskryf as (2(x + 2x + 3))/2 en sodoende te vereenvoudig x + 2x + 3. Let wel, jy kan nie elke term uitskakel nie - net daardie faktore wat in beide die teller en die noemer is. Byvoorbeeld, die uitdrukking (x(x + 2))/x, waar die "X" kan uit die breuk verwyder word, en laat (x + 2)/1 = (x + 2). Maar (x + 2)/x is nie om te vereenvoudig tot 2/1 = 2. 
Byvoorbeeld, die uitdrukking 3(x + 8 kan vereenvoudig word na3x + 24, terwyl 3x(x + 8) vereenvoudig kan word na 3x + 24x. Let daarop dat in sommige gevalle, soos met veranderlike breuke, die konstante buite die hakies in die vereenvoudiging gebruik kan word en dus nie vermenigvuldig moet word nie. Byvoorbeeld, in die breuk (3(x + 8))/3x kom die faktor 3 in beide die teller en die noemer voor, dus kan ons dit kanselleer en die uitdrukking vereenvoudig tot (x + 8)/x. Dit is eenvoudiger en makliker om mee te werk as met (3x + 24x)/3x, wat die antwoord sou gewees het as ons vermenigvuldig het. 
Kyk weer na die uitdrukking x - 5x + 6. Dit kan opgelos word in (x - 3) (x - 2). So as x - 5x + 6 die teller is van `n vergelyking met een van hierdie faktore in die noemer (soos in (x - 5x + 6)/(2(x - 2))), dan kan ons dit in faktore soos dat ons van die noemer ontslae kan raak. Met ander woorde, by (x - 3)(x - 2)/(2(x - 2)), (x - 2) val uit, wat ons verlaat(x - 3)/2 oorgebly het. Soos hierbo aangedui, kan jy ook `n vergelyking met faktorisering oplos, veral as dit gelyk aan nul gestel is. Byvoorbeeld: neem die vergelyking x - 5x + 6 = 0. Faktorering gee ons (x - 3)(x - 2) = 0. Aangesien `n getal maal nul gelyk is aan nul, kan ons beide terme gelyk aan nul stel om die antwoord op hierdie probleem te vind. Die antwoord op die vergelyking is dus x=3 en x= 2.
Vereenvoudiging van wiskundige uitdrukkings
Inhoud
Wiskundeprobleme vra dikwels vir `n antwoord "so eenvoudig as moontlik" om neer te skryf — met ander woorde, om so elegant as moontlik `n antwoord te gee. Terwyl `n lang, lomp uitdrukking en `n korter, meer elegante weergawe daarvan tegnies dieselfde beteken, word `n antwoord dikwels nie aanvaar voordat dit so ver as moontlik vereenvoudig is nie.Boonop is vereenvoudigde antwoorde ook makliker om mee te werk. `Dit is hoekom leer om te vereenvoudig `n noodsaaklike vaardigheid vir toekomstige wiskundiges is.
Trappe
Metode 1 van 2: Die volgorde van wiskundige bewerkings

1. Die volgorde van operasies. Wanneer jy wiskundige uitdrukkings vereenvoudig, kan jy nie net van links na regs evalueer nie. Sekere operasies geniet voorrang bo ander en moet dus eers gedoen word. As jy dit nie doen nie, kan jy die verkeerde antwoord kry. Die volgorde van bewerkings in wiskunde is soos volg: Hakies, Eksponensiëring en wortels, Vermenigvuldiging en deling, Optel en aftrek. `n Mnemoniek om hierdie volgorde te onthou is "Hoe moet ons ontslae raak van die onvoldoende " of "HMWVDOA".
- Let daarop dat hoewel `n basiese kennis van die bewerkings voldoende is om die meeste standaard uitdrukkings op te los, is spesiale tegnieke nodig om uitdrukkings op te los wat veranderlikes bevat, insluitend die meeste polinome. Kyk na Metode Twee vir meer inligting.

2. Begin deur alle terme tussen hakies op te los. In wiskunde beteken hakies dat alle terme wat hulle insluit apart van die omringende uitdrukking opgelos moet word. Ongeag die bewerkings, maak seker dat jy eers alle terme binne hakies oplos as jy `n uitdrukking wil vereenvoudig. Hou in gedagte dat die berekeningsreëls vir die volgorde van bewerkings ook binne hakies geld. So ook hier eers hakies, dan eksponensiëring, ens.

3. Los nou die magte op. Nadat u die hakies uitgewerk het, kan u nou voortgaan met eksponensiëring. Los hulle een vir een op.

4. Los nou die vermenigvuldigingssomme op. Onthou dat `n vermenigvuldiging op verskeie maniere geskryf kan word. Met `n punt, sonder `n punt, of met `n ×-simbool. Maar ook iets soos 4(x)) dui op `n vermenigvuldiging.

5. Gaan voort met verdeelprobleme. As jy verdelingsprobleme soek, onthou dat dit ook op verskillende maniere geskryf kan word. Die eenvoudige ÷ simbool , met `n dubbelpunt, of `n skuinsstreep (soos 3/4) dui almal `n verdeling aan.

6. Tel op. Tel nou die verskillende terme by. Werk dit van links na regs uit, soos dit in die uitdrukking is en wat ook al die gerieflikste is. Byvoorbeeld, in die som 49 + 29 + 51 +71 is dit makliker om die probleem in die volgende blokke te verdeel: 49 + 51 = 100, 29 + 71 = 100 en 100 + 100 = 200. Dit is makliker as 49 + 29 = 78, 78 + 51 = 129 en 129 + 71 = 200.

7. aftrek. Die laaste stap van die bewerkings is om die oorblywende terme af te trek. Werk die res van jou uitdrukking uit, van links na regs. Jy kan die byvoeging van negatiewe getalle in hierdie of die vorige stap doen – dit maak nie saak vir jou antwoord nie.

8. Kyk na jou uitdrukking. Nadat u deur die volgorde van bewerkings gewerk het, het u `n aantal terme in die mees vereenvoudigde vorm. As daar een of meer veranderlikes in die uitdrukking is, bly hulle grootliks onveranderd. Om uitdrukkings met veranderlikes te vereenvoudig, vereis dat ons hierdie vergelykings verder oplos vir die onbekendes, of spesiale metodes gebruik (sien volgende stap).
Metode 2 van 2: Vereenvoudig komplekse uitdrukkings

1. Voeg gelyke veranderlike magte bymekaar. Wanneer ons te doen het met uitdrukkings wat veranderlikes bevat, is dit belangrik om te onthou dat terme met dieselfde veranderlike en dieselfde eksponent (of "gelyke terme") kan saamgetel (of afgetrek) word soos gewone getalle. Die terme moet het nie net dieselfde veranderlike nie, maar ook dieselfde eksponent. Byvoorbeeld, 7x en 5x kan saamgetel word, maar 7x en 5x kan nie.
- Hierdie reël kan ook uitgebrei word na meerveranderlike terme. Byvoorbeeld, 2xy kan by -3xy gevoeg word, maar nie -3xy of -3y nie.
- Neem die volgende uitdrukkings: x + 3x + 6 - 8x. In hierdie uitdrukking kan ons die terme 3x en -8x bymekaar tel, want hulle is gelyk aan mekaar. Ons uitdrukking word dan vereenvoudig: x - 5x + 6.

2. Vereenvoudig breuke deur faktore uit te skakel of te deel. Breuke wat slegs uit getalle (en geen veranderlikes) bestaan, kan op verskeie maniere vereenvoudig word. `n Breuk is net `n deelsom en moet as sodanig hanteer word. Daarbenewens, as dieselfde vermenigvuldiging in die teller of noemer voorkom, kan dit uitgeskakel word, want hulle gee reeds antwoord 1 wanneer dit gedeel word. Met ander woorde, as die teller en noemer albei dieselfde faktor het, kan dit uit die breuk verwyder word, wat die resultaat vereenvoudig.

3. As jy te doen het met breuke wat veranderlikes bevat, probeer om die veranderlikes uit te skakel. Hierdie uitdrukkings bied unieke moontlikhede om te vereenvoudig. Soos gewone breuke, laat veranderlike breuke jou toe om faktore te verwyder wat in beide die teller en noemer is. Maar in laasgenoemde geval kan hierdie faktore getalle sowel as veranderlikes wees.

4. Vermenigvuldig die terme tussen hakies met hul konstantes. Wanneer ons met veranderlike terme tussen hakies plus `n konstante handel, kan die vermenigvuldiging van enige term binne die hakies met die konstante buite die hakies `n eenvoudiger uitdrukking tot gevolg hê.Dit geld vir beide numeriese konstantes en konstantes met veranderlikes.

5. Vereenvoudig deur faktorisering. Dit is `n tegniek wat sommige vergelykings kan vereenvoudig. Wanneer jy faktoriseer, dink aan iets waarvan die teenoorgestelde is "hakies vermenigvuldig" – soms kan `n vergelyking eenvoudiger voorgestel word as twee terme vermenigvuldig met mekaar as as een vergelyking. Dit is veral waar as jy `n deel van die vergelyking daarmee kan uitskakel. In sekere gevalle (soos met kwadratiese vergelykings) kan jy ook die vergelyking self oplos met faktorisering.
Artikels oor die onderwerp "Vereenvoudiging van wiskundige uitdrukkings"
Оцените, пожалуйста статью
Gewilde