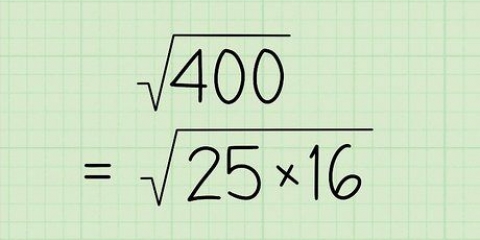Hoe om te kyk of 'n getal Prime is

Inhoud

Trappe
Wenke
Benodigdhede

Priemgetalle is getalle wat slegs deur hulself deelbaar is en 1 genoem word – ander getalle samestelling getalle. Wanneer dit kom by die toets of `n getal priemgetal is, is daar verskeie opsies. Sommige van hierdie metodes is relatief eenvoudig, maar beslis nie prakties vir groter getalle nie. Ander toetse wat dikwels gebruik word, is eintlik volledige algoritmes gebaseer op a waarskynlikheid wat soms verkeerdelik `n getal as priemgetal klassifiseer. Lees verder by stap 1 om te leer hoe om jouself te toets of jy met `n priemgetal te doen het.

Trappe

Metode 1 van 4: Probeer deur te deel

Om te probeer deur te deel is verreweg die maklikste manier om `n getal te toets. Vir klein getalle is dit gewoonlik ook die vinnigste manier. Die toets is gebaseer op die definisie van `n priemgetal: `n getal is priemgetal as dit net deur homself en 1 deelbaar is.

Prent getiteld Kyk of `n nommer eerste is Stap 1

1. Paar n is die nommer wat jy wil toets. Deel die getal n deur alle moontlike deelbare heelgetalle. Vir groter getalle soos n=101 is dit uiters onprakties om te deel deur elke moontlike heelgetal kleiner as n. Gelukkig is daar verskeie truuks om die aantal faktore wat getoets moet word, te verminder.

Prent getiteld Kyk of `n nommer eerste is Stap 2

2. Bepaal of n selfs is. Alle ewe getalle is volledig deelbaar deur 2. Daarom, as n ewe is, kan jy dit sê n is `n saamgestelde getal (en dus nie `n priemgetal nie). Om vinnig te bepaal of `n getal ewe is, moet jy net aandag gee aan die laaste syfer. As die laaste syfer 2, 4, 6, 8 of 0 is, dan is die getal ewe en nie priemgetal nie.

Die enigste uitsondering op hierdie reël is die getal 2 self, wat, omdat dit deur homself en 1 deelbaar is, ook priemgetal is. 2 is die enigste ewe priemgetal.

Prent getiteld Kyk of `n nommer eerste is Stap 3

3. Deel n met enige getal tussen 2 en n-1. Aangesien `n priemgetal geen ander faktore as homself en 1 het nie en omdat faktore van heelgetalle minder as hul produk is, sal die nagaan van die deelbaarheid van `n heelgetal kleiner as n en groter as 2 bepaal of n priemgetal is. Ons begin na 2 omdat ewe getalle (veelvoude van 2) nie priemgetalle kan wees nie. Dit is ver van `n doeltreffende manier om te toets, soos u hieronder sal sien.

As ons byvoorbeeld hierdie metode wil gebruik om te toets of 11 priemgetal is of nie, sal ons 11 deur 3, 4, 5, 6, 7, 8, 9 en 10 moet deel, elke keer op soek na `n heelgetalantwoord sonder res. Aangesien nie een van hierdie getalle heeltemal by 11 pas nie, kan ons sê dat 11 a is prima is.

Prent getiteld Kyk of `n nommer eerste is Stap 4

4. Om tyd te bespaar, toets slegs tot sqrt(n), afgerond. Om `n getal n te toets deur alle getalle tussen 2 en n-1 te kontroleer, kan vinnig baie tydrowend raak. Byvoorbeeld, as ons met hierdie metode wil kyk of 103 priem is, sal ons deur 3, 4, 5, 6, 7 moet deel ... ens., tot by 102! Gelukkig is dit nie nodig om so te toets nie. In die praktyk is dit slegs nodig om te toets deur die faktore tussen 2 en die vierkantswortel van n. As die vierkantswortel van n nie `n getal is nie, rond dit af tot die naaste heelgetal en toets tot hierdie getal. Sien hieronder vir `n verduideliking:

Kom ons ondersoek die faktore van 100. 100 = 1 × 100, 2 × 50, 4 × 25, 5 × 20, 10 × 10, 20 × 5, 25 × 4, 50 × 2 en 100 × 1. Let daarop dat na 10 × 10, die faktore dieselfde is as vir 10 × 10, slegs omgekeerd. Oor die algemeen kan ons die faktore van n groter as sqrt(n) ignoreer omdat hulle bloot `n voortsetting is van faktore kleiner as sqrt(n).

Kom ons probeer `n voorbeeld. As n = 37, hoef ons nie alle getalle van 3 tot 36 te toets om te bepaal of n priemgetal is nie. In plaas daarvan hoef ons net na die getalle tussen 2 en sqrt(37) (afgerond) te kyk.

sqrt(37) = 6.08 – ons gaan dit na 7 afrond.

37 is nie volledig deelbaar deur 3, 4, 5, 6 en 7 nie en daarom kan ons met vertroue sê dat dit `n priemgetal is.

Prent getiteld Kyk of `n nommer eerste is Stap 5

5. Om nog meer tyd te bespaar, gebruik ons net prima faktore. Dit is moontlik om die proses van toetsing deur deling nog korter te maak deur nie daardie faktore in te sluit wat nie priemgetalle is nie. Per definisie kan enige saamgestelde getal uitgedruk word as die produk van twee of meer priemgetalle. Dit is dus onnodig om die getal n deur `n saamgestelde getal te deel - dit is gelykstaande aan `n paar keer deur priemgetal te deel. Dus, ons kan die lys van moontlike faktore verder beperk tot slegs priemgetalle kleiner as sqrt(n).

Dit beteken dat alle ewe faktore, sowel as dié wat veelvoude van priemgetalle is, oorgeslaan kan word.

Byvoorbeeld, kom ons probeer vasstel of 103 priem is of nie. Die vierkantswortel van 103 is 11 (na bo). Die priemgetalle tussen 2 en 11 is 3, 5, 7 en 11. 4, 6, 8 en 10 is ewe en 9 is `n veelvoud van 3, `n priemgetal, so ons kan hierdie een oorslaan. Deur dit te doen, het ons ons lys van moontlike faktore tot net 4 nommers verminder!

103 is nie volledig deelbaar deur 3, 5, 7 of 11 nie, so ons weet nou dat 103 `n priemgetal is.

Metode 2 van 4: Gebruik Fermat . se klein stelling

In 1640 het die Franse wiskundige Pierre de Fermat vir die eerste keer `n stelling (wat nou na hom vernoem is) gestel wat baie nuttig kan wees om te bepaal of `n getal priemgetal is of nie. Tegnies is Fermat se toets bedoel om te kyk of `n getal saamgestel is, eerder as priem. Dit is omdat die toets met "absolute sekerheid" kan wys dat `n getal saamgestel is, maar slegs a "waarskynlikheid" of `n getal priemgetal is. Fermat se klein stelling is nuttig in situasies waar dit nie prakties is om deur te deel nie en wanneer `n lys getalle beskikbaar is wat uitsonderings op die stelling is.

Prent getiteld Kyk of `n nommer eerste is Stap 6

1. Veronderstel n die nommer is vir toetsing. Jy gebruik hierdie toets om te bepaal of `n gegewe getal n priemgetal is. Maar soos hierbo genoem, kan hierdie stelling soms verkeerdelik sekere samestellings as priemgetal karakteriseer. Dit is belangrik om dit in ag te neem en jou antwoord na te gaan, wat later verduidelik sal word.

Prent getiteld Kyk of `n nommer eerste is Stap 7

2. Kies `n heelgetal a tussen 2 en n-1 (insluitend). Die presiese heelgetal wat jy kies is nie belangrik nie. Aangesien die parameters vir a 2 en n-1 insluit, kan jy dit ook gebruik.

`n Voorbeeld: Is 100 `n priemgetal of nie?. Gestel ons neem 3 as toetswaarde - dit is tussen 2 en n-1, so dit is voldoende.

Prent getiteld Kyk of `n nommer eerste is Stap 8

3. bereken a (mod n). Om hierdie uitdrukking uit te werk, vereis `n mate van kennis van `n wiskundige stelsel genoem modulêre wiskunde. In modulêre wiskunde keer getalle terug na nul wanneer `n sekere waarde, bekend as die, bereik word modulus. Jy kan hieraan dink soos `n horlosie: uiteindelik sal die klokwyser terugskiet na 1 uur na 12 uur, nie na 1 uur nie. Die modulus word aangedui as (mod n). So by hierdie stap bereken jy met `n modulus van n.

Nog `n metode is om a te bereken en dan deur n te deel, en gebruik dan die res as jou antwoord. Gespesialiseerde sakrekenaars met `n modulusfunksie kan baie nuttig wees wanneer groot getalle gedeel word, omdat hulle die res van `n deling direk kan bereken.

Deur so `n sakrekenaar in ons voorbeeld te gebruik, kan ons sien dat 3/100 `n res van 1 het. Dus, 3 (mod 100) is 1.

Prent getiteld Kyk of `n nommer eerste is Stap 9

4. As ons dit met die hand bereken, gebruik ons die eksponent as kort notasie. As jy nie `n sakrekenaar met `n modulusfunksie het nie, gebruik eksponensiële notasie om die prosedure om die res te bepaal makliker te maak. Sien onder:

In ons voorbeeld bereken ons 3 met `n modulus van 100. 3 is `n baie, baie groot getal - 515,377,520,732,011,331,036,461,129,765,621,272,702,107,522,001 - so groot dat dit baie moeilik word om mee te werk. Eerder as om die 48-syfer-antwoord vir 3 te gebruik, sal ons dit beter as `n eksponent skryf, dus ((((((3)*3))))*3)). Onthou dat die neem van die eksponent van `n eksponent die effek gee van die vermenigvuldiging van die eksponente ((x) = x).

Nou kan ons die res bepaal. Begin oplos vir (((((((3)*3))))*3)) by die binneste stel hakies en werk jou pad uit, deel elke stap deur 100. Sodra ons die res gevind het, sal ons dit vir die volgende stap gebruik in plaas van as die werklike antwoord. Sien onder:

((((((9)*3))))*3)) - 9/100 het geen res nie, so ons kan voortgaan.

(((((((27))))*3)) - 27/100 het geen res nie, so ons kan voortgaan.

(((((729)))*3)) - 729/100 = 7 R 29. Ons res is 29. Ons gaan aan na die volgende stap, nie 729 nie.

((((29=841))*3)) - 841/100 = 8 R 41. Ons sal ons res 41 weer gebruik in die volgende stap.

(((41 = 1681)*3)) - 1681/100 = 16 R 81. Ons sal ons res 81 in die volgende stap gebruik.

((81*3 = 243)) - 243/100 = 2 R 43. Ons sal ons res 43 in die volgende stap gebruik.

(43 = 1849) - 1849/100 = 18 R 49. Ons sal ons res 49 in die volgende stap gebruik.

49 = 2401 - 2401/100 = 24 R 1. ons finale res is 1. Met ander woorde, 3 (mod 100) = 1. Let daarop dat dit dieselfde antwoord is wat ons in die vorige stap bereken het!

Prent getiteld Kyk of `n nommer eerste is Stap 10

5. Kyk of a (mod n) = a (mod n). Indien nie, dan is n saamgestel. As dit waar is, dan is n waarskynlik, (maar nie seker nie) `n priemgetal. Die herhaling van die toets met verskillende waardes vir `n kan die uitkoms meer seker maak, maar daar is seldsame saamgestelde getalle wat aan Fermat se stelling vir almal waardes van a. Dit word die Carmichael-getalle genoem - die kleinste van hierdie getalle is 561.

In ons voorbeeld, 3 (mod 100) = 1 en 3 (mod 100) = 3. 1 ≠ 3, dus kan ons sê dat 100 `n saamgestelde getal is.

6. Gebruik die Carmichael-nommers om seker te wees van jou uitkoms. Om te weet watter getalle aan die Carmichael-volgorde voldoen voordat jy voortgaan, kan jou baie kopsere spaar oor die vraag of `n getal priemgetal is of nie. Oor die algemeen is Carmichael-getalle die produk van individuele priemgetalle, waar dit vir alle priemgetalle geld dat as p `n deler van n is, dan is p-1 ook `n deler van n-1. Die aanlyn lys van Carmichael-getalle kan baie nuttig wees om te bepaal of `n getal priem is deur Fermat se klein stelling te gebruik.

Metode 3 van 4: Gebruik die Miller-Rabin-toets

Die Miller-Rabin-toets werk op dieselfde manier as Fermat se klein stelling, maar hanteer anomale getalle soos Carmichael-getalle op `n beter manier.

Prent getiteld Kyk of `n nommer eerste is Stap 12

1. Paar n is `n onewe getal wat ons vir primaliteit wil toets. Soos in die metodes hierbo aangedui, is n die veranderlike waarvan ons die primaliteit wil bepaal.

Prent getiteld Kyk of `n nommer eerste is Stap 13

2. Besig n-1 af in die vorm 2 × d waardeur d is vreemd. Die getal n is priemgetal as dit onewe is. So n - 1 moet ewe wees. Aangesien n - 1 ewe is, kan dit geskryf word as `n mag van 2 keer `n onewe getal . Dus,4 = 2 × 1; 80 = 2 × 5; en so aan.

Gestel ons wil bepaal of n = 321 `n priemgetal is. 321 - 1 = 320, wat ons kan uitdruk as 2×5.

In hierdie geval is n = 321 `n geskikte getal. Die bepaling van n – 1 vir n = 371 kan `n groot waarde vir d vereis, wat die hele proses in `n later stadium moeiliker maak. 371 - 1 = 370 = 2 × 185

Prent getiteld Kyk of `n nommer eerste is Stap 14

3. Kies enige nommer a tussen 2 en n-1. Die presiese getal wat jy kies maak nie saak nie – net dat dit minder as n en groter as 1 moet wees.

In ons voorbeeld met n = 321, kies ons a = 100.

Prent getiteld Kyk of `n nommer eerste is Stap 15

4. bereken a (mod n). as a = 1 of -1 (mod n), dan weerstaann die Miller-Rabin-toets en is waarskynlik `n priemgetal. Soos met Fermat se Klein Stelling, kan hierdie toets nie die primaliteit van `n getal met absolute sekerheid bepaal nie, maar het addisionele toetse nodig om dit te doen.

In ons voorbeeld met n = 321, a (mod n) = 100 (mod 321). 100 = 10 000 000 000 (mod 321) = 313. Ons gebruik `n spesiale sakrekenaar, of die snelskrifmetode met `n eksponent soos vroeër beskryf, om die res van 100/321 te vind.

Aangesien ons nie 1 of -1 gekry het nie, kan ons nie met sekerheid sê dat n priem is nie. Maar daar is meer wat ons moet doen – lees verder.

Prent getiteld Kyk of `n nommer eerste is Stap 16

5. Aangesien die resultaat nie gelyk is aan 1 of -1 nie, berekena, a,... en so aan, tot ad. Bereken a tot die mag van d keer, tot 2. As een van hierdie gelyk is aan 1 of -1 (mod n), dan weerstaan n die Miller-Rabin-toets en is waarskynlik prima. Sodra jy vasgestel het dat n die toets slaag, kontroleer dan jou antwoord (sien die stap hieronder). As n nie enige van hierdie toetse slaag nie, dan is dit a saamgestel nommer.

Ter herinnering, in ons voorbeeld is die waarde van a gelyk aan 100, die waarde van s is 6 en van d5. Ons sal voortgaan met toetsing soos hieronder aangedui:

100 = 1×10.

1×10 (mod 321) = 64. 64 ` 1 of -1. Bly kalm.

100 = 1×10.

1×10 (mod 321) = 244. 244 ≠ 1 of -1.

Op hierdie punt kan ons stop. s - 1 = 6 - 1 = 5. Ons het nou 4d = 2 bereik, en daar is geen magte van 2 maal d onder 5d nie. Aangesien geen van ons berekeninge `n 1 of -1 as `n antwoord gegee het nie, kan ons sê dat n = 321 a saamgestel nommer is.

Prent getiteld Kyk of `n nommer eerste is Stap 17

6. as n voldoen aan die Miller-Rabin-toets, herhaal dan vir die ander waardes van a. As jy gevind het dat die waarde van n wel priemgetal kan wees, probeer weer met `n ander ewekansige waarde vir a om die resultaat van die toets te bevestig. As n eintlik priem is, sal dit geld vir enige waarde van a. As n `n saamgestelde getal is, sal dit vir driekwart van die waardes van a misluk. Dit gee jou meer sekerheid as met Fermat se Klein Stelling, waarin sekere saamgestelde getalle (die Carmichael-getalle) die toets slaag vir elke waarde van `n.

Metode 4 van 4: Gebruik die Chinese resstelling

Prent getiteld Kyk of `n nommer eerste is Stap 18

1. Kies twee nommers. Een van die getalle is nie priemgetal nie en die tweede is die getal wat vir primaliteit getoets word.

"toets nommer 1" = 35
Toetsnommer2 = 97

Prent getiteld Kyk of `n nommer eerste is Stap 19

2. Kies twee datapunte groter as nul en minder as Toetsnommer1, onderskeidelik Toetsnommer2. Hulle kan nie dieselfde wees nie.

Data1 = 1

Data2 = 2

Prent getiteld Kyk of `n nommer eerste is Stap 20

3. Bereken die MMI (Mathematical Multiplicative Inverse) vir Toetsnommer1 en Toetsnommer2

Bereken die MMI

MMI1 = Toetsnommer2 ^ -1 Mod Toetsnommer1

MMI2 = Toetsnommer1 ^ -1 Mod Toetsnommer2

Slegs vir priemgetal (daar sal `n resultaat wees vir nie-prime, maar dit is nie die MMI nie):

MMI1 = (Toetsnommer2 ^ (Toetsnommer1-2)) %Toetsnommer1

MMI2 = (Toetsnommer1 ^ (Toetsnommer-2)) % Toetsnommer2

Dus:

MMI1 = (97^33) %35

MMI2 = (35^95) %97

Prent getiteld Kyk of `n nommer eerste is Stap 21

4. Skep `n binêre tabel vir elke MMI tot Log2 van die Modulus

Vir die MMI1

F(1) = Toetsnommer2 % Toetsnommer1 = 97 % 35 = 27

F(2) = F(1) * F(1) % Toetsnommer1 = 27 * 27 % 35 = 29

F(4) = F(2) * F(2) % Toetsnommer1 = 29 * 29 % 35 = 1

F(8) = F(4) * F(4) % Toetsnommer1 = 1 * 1 % 35 = 1

F(16) =F(8) * F(8) % Toetsnommer1 = 1 * 1 % 35 = 1

F(32) = F(16) * F(16) % Toetsnommer1 = 1 * 1 % 35 = 1

Bereken die binêre logaritme van Toetsnommer1 - 2

35 -2 = 33 (10001) basis 2

MMI1 = F(33) = F(32) * F(1) mod 35

MMI1 = F(33) = 1 * 27 Mod 35

MMI1 = 27

Vir MMI2

F(1) = Toetsnommer1 % Toetsnommer2 = 35 % 97 = 35

F(2) = F(1) * F(1) % Toetsnommer2 = 35 * 35 mod 97 = 61

F(4) = F(2) * F(2) % Toetsnommer2 = 61 * 61 mod 97 = 35

F(8)= F(4) * F(4) % Toetsnommer2 = 35 * 35 mod 97 = 61

F(16) = F(8) * F(8) % Toetsnommer2 = 61 * 61 mod 97 = 35

F(32)= F(16) * F(16) % Toetsnommer2 = 35 * 35 mod 97 = 61

F(64)= F(32) * F(32) % Toetsnommer2 = 61 * 61 mod 97 = 35

F(128) = F(64) * F(64) % Toetsnommer2 = 35 * 35 mod 97 = 61

Bereken die binêre logaritme van Toetsnommer2 - 2

97 - 2 = 95 = (1011111) basis 2

MMI2 = (((((F(64) * F(16) % 97) * F(8) % 97) * F(4) % 97) * F(2) % 97) * F(1) % 97 )

MMI2 = ((((((35 * 35) %97) * 61) % 97) * 35% 97) * 61% 97) * 35% 97)

MMI2 = 61

Prent getiteld Kyk of `n nommer eerste is Stap 22

5. Bereken (Data1 * Toetsnommer2 * MMI1 + Data2 * Toetsnommer1 * MMI2) % (Toetsnommer1 * Toetsnommer)

Antwoord = (1 * 97 * 27 + 2 * 35 * 61) % (97 * 35)

Antwoord = (2619 + 4270) % 3395

Antwoord = 99

Prent getiteld Kyk of `n nommer eerste is Stap 23

6. Kyk of "toets nommer 1" is nie priem 1 nie

Bereken (Antwoord - Data1) % Toetsnommer1

99 -1 % 35 = 28

Aangesien 28 groter as 0 is, is 35 nie priemgetal nie

Prent getiteld Kyk of `n nommer eerste is Stap 24

7. Kyk of Toetsnommer2 `n priemgetal is

Bereken (Antwoord - Data2) % Toetsnommer2

99 - 2% 97 = 0

Aangesien 0 gelyk is aan 0, is 97 `n potensiële priemgetal

Prent getiteld Kyk of `n nommer eerste is Stap 25

8. Herhaal stappe 1 tot 7 ten minste nog twee keer.

As stap 7 gelyk is aan 0:

Gebruik `n ander "toets nommer 1" as Toetsnommer1 nie priemgetal is nie.

Gebruik `n ander Toetsnommer1 waar `n Toetsnommer1 eintlik `n priemgetal is.In hierdie geval is stappe 6 en 7 gelyk aan 0.

Gebruik verskillende datapunte vir data1 en data2.

As stap 7 altyd gelyk is aan 0, dan is die waarskynlikheid dat getal2 priem is, baie hoog.

Dit is bekend dat stappe 1 tot 7 verkeerd is in sekere gevalle wanneer die eerste getal nie priemgetal is nie en die tweede `n priemfaktor van die nie-priemgetal is "toets nommer 1".Dit werk in alle scenario`s waar beide getalle priemgetalle is.

Die rede waarom stappe 1 tot 7 herhaal word, is omdat daar `n paar scenario`s is waar, selfs al is Toetsnommer1 nie priemgetal nie en Toetsnommer2 nie priemgetal nie, enige getal van Stap 7 steeds nul is.Hierdie toestande is skaars.Deur Toetsnommer1 na `n ander nie-priemgetal te verander, as Toetsnommer2 nie priemgetal is nie, sal Toetsnommer2 nie meer gelyk wees aan nul nie, in stap 7. Met die uitsondering van die geval waar "toets nommer 1" `n faktor van ToetsGetal2 is, sal priemgetalle altyd nul wees in stap 7.

Wenke

Die 168 priemgetalle onder 1000 is: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79 , 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157. , 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293. , 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461. , 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607. , 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 812, 8, 8, 8, 8, 8, 8, 3 , 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 9
Wanneer probeer om te verdeel stadiger is as die meer gesofistikeerde metodes, is dit steeds doeltreffend vir kleiner getalle. Selfs wanneer groter getalle getoets word, is dit nie ongewoon om eers die klein getalle na te gaan voordat na die meer gevorderde metodes oorgeskakel word nie.