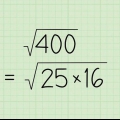is `die absolute waarde van 2.`
is `die absolute waarde van 2.`



Opdrag:
Vereenvoudig binne hakies:
Optel en aftrek:
Maak alles binne die absolute waarde positief:
Finale antwoord: 19 
Opdrag:
Doen die volgorde van bewerkings binne en buite die absolute waarde:
Bepaal die absolute waardes:
Orde van operasies:
Vereenvoudig die finale antwoord: 

 =
= 
 =
= 
 =
= 


 = (1, 6)
= (1, 6) = (2, -1)
= (2, -1) = (-8, 6)
= (-8, 6)

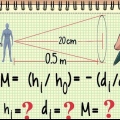
Koëffisiënte: (3, -4) Afstand Formule:
Kwadra die koëffisiënte: ` 
Gee aandag: Oefen die afstandformule weer as jy dit nie verstaan nie. Let daarop dat die kwadraat van beide getalle hulle positief maak, wat jou in wese die absolute waarde gee. 
Koëffisiënte: (3, -4) Afstand Formule:
Kwadra die koëffisiënte:
Voeg die produk van die koëffisiënte bymekaar:

Koëffisiënte: (3, -4) Afstand Formule:
Kwadra die koëffisiënte:
Voeg die produk van die koëffisiënte bymekaar:
Trek die vierkantswortel af vir die finale antwoord: 5 

 = √37
= √37 = √5
= √5 = 10
= 10
Bereken die absolute waarde van 'n getal
Inhoud
Die absolute waarde van `n getal is maklik om te vind, en die teorie daaragter is belangrik vir die oplossing van vergelykings met `n absolute waarde. Elke absolute waarde is `n maatstaf van hoe ver daardie getal van nul is. As jy aan `n getallelyn dink, met die nul in die middel, kan jy uitvind hoe ver die betrokke getal van daardie nul af is.
Trappe
Metode 1 van 2: Bepaal absolute waarde

1. Onthou dat die absolute waarde die afstand van `n getal vanaf nul is. `n Absolute waarde is die afstand van die getal tot nul langs `n getallelyn. óf, dui dus eenvoudig aan hoe ver weg -4 van nul is. Aangesien afstand altyd `n posisienommer is (jy kan nie in `negatiewe` stappe beweeg nie, net in `n ander rigting), is die resultaat van die absolute waarde altyd positief.
dui dus eenvoudig aan hoe ver weg -4 van nul is. Aangesien afstand altyd `n posisienommer is (jy kan nie in `negatiewe` stappe beweeg nie, net in `n ander rigting), is die resultaat van die absolute waarde altyd positief.
 dui dus eenvoudig aan hoe ver weg -4 van nul is. Aangesien afstand altyd `n posisienommer is (jy kan nie in `negatiewe` stappe beweeg nie, net in `n ander rigting), is die resultaat van die absolute waarde altyd positief.
dui dus eenvoudig aan hoe ver weg -4 van nul is. Aangesien afstand altyd `n posisienommer is (jy kan nie in `negatiewe` stappe beweeg nie, net in `n ander rigting), is die resultaat van die absolute waarde altyd positief.
2. Maak die getal binne die absolute waardebalkies positief. Eenvoudig gestel, die absolute waarde maak enige getal positief. Dit is nuttig om afstand te meet, of waardes in finansiële sake te bepaal, om met negatiewe getalle soos skuld of lenings te werk.

3. Gebruik eenvoudige, vertikale stawe om `n absolute waarde aan te dui. Die formaat vir `n absolute waarde is maklik. Enkele reëls (gevind naby die Enter-sleutel op `n sleutelbord) om `n getal of uitdrukking, soos  , dui op `n absolute waarde.
, dui op `n absolute waarde.
 , dui op `n absolute waarde.
, dui op `n absolute waarde. is `die absolute waarde van 2.`
is `die absolute waarde van 2.`
4. Laat minustekens vir die getal binne die absolute waardemerke weg. Byvoorbeeld: |-5| word dan |5|.

5. Laat die absolute waarde punte weg. Die getal wat oorbly is die antwoord, dus |-5| word |5| en toe 5. Die volgende is al wat jy hoef te doen:


6. Vereenvoudig die uitdrukking binne die absolute waarde. Is dit `n eenvoudige uitdrukking, soos  , dan kan jy dit net positief maak. Maar `n uitdrukking soos
, dan kan jy dit net positief maak. Maar `n uitdrukking soos  moet vereenvoudig word voordat jy die absolute waarde daarvan kan vind. Die vaste volgorde van operasies geld steeds:
moet vereenvoudig word voordat jy die absolute waarde daarvan kan vind. Die vaste volgorde van operasies geld steeds:
 , dan kan jy dit net positief maak. Maar `n uitdrukking soos
, dan kan jy dit net positief maak. Maar `n uitdrukking soos  moet vereenvoudig word voordat jy die absolute waarde daarvan kan vind. Die vaste volgorde van operasies geld steeds:
moet vereenvoudig word voordat jy die absolute waarde daarvan kan vind. Die vaste volgorde van operasies geld steeds:




7. Gebruik altyd hierdie volgorde van bewerkings voordat die absolute waarde bereken word. Wanneer jy langer vergelykings uitwerk, doen jy al die vereiste werk voordat jy die absolute waarde bepaal. Moenie probeer om absolute waardes te vereenvoudig totdat alles korrek opgetel, afgetrek en gedeel is nie. Byvoorbeeld:






8. Hou aan om aan `n paar voorbeeldoefeninge te werk om dit onder die knie te kry. Om die absolute waarde van `n getal te bereken is baie maklik, maar dit beteken nie dat oefenprobleme nie nuttig sal wees om jou kennis op te knap nie:
 =
= 
 =
= 
 =
= 
Metode 2 van 2: Los komplekse vergelykings op met absolute waardes (vergelykings met `i`)

1. Wees versigtig wanneer jy met komplekse vergelykings handel wat denkbeeldige getalle behels, soos `i` of - 1  , en los dit afsonderlik op. Jy kan nie die absolute waarde van denkbeeldige getalle vind op dieselfde manier as wat jy rasionale getalle kan vind nie. Jy kan die absolute waarde van `n komplekse vergelyking vind deur dit in die afstandformule uit te werk. Neem die uitdrukking
, en los dit afsonderlik op. Jy kan nie die absolute waarde van denkbeeldige getalle vind op dieselfde manier as wat jy rasionale getalle kan vind nie. Jy kan die absolute waarde van `n komplekse vergelyking vind deur dit in die afstandformule uit te werk. Neem die uitdrukking  as `n voorbeeld.
as `n voorbeeld.
 , en los dit afsonderlik op. Jy kan nie die absolute waarde van denkbeeldige getalle vind op dieselfde manier as wat jy rasionale getalle kan vind nie. Jy kan die absolute waarde van `n komplekse vergelyking vind deur dit in die afstandformule uit te werk. Neem die uitdrukking
, en los dit afsonderlik op. Jy kan nie die absolute waarde van denkbeeldige getalle vind op dieselfde manier as wat jy rasionale getalle kan vind nie. Jy kan die absolute waarde van `n komplekse vergelyking vind deur dit in die afstandformule uit te werk. Neem die uitdrukking  as `n voorbeeld.
as `n voorbeeld. - Opdrag:
- Gee aandag: As jy `n uitdrukking gebruik soos
jy kan dit vervang met `i.` Die vierkantswortel van -1 is `n denkbeeldige getal, i.

2. Vind die koëffisiënte van die komplekse vergelyking. Neem 3-4i as die vergelyking van `n lyn. Die absolute waarde is die afstand tot nul, so jy bepaal die afstand na nul vir die punt (3, -4) op hierdie lyn.Die koëffisiënte is bloot die twee getalle wat nie `i` is nie. Alhoewel die getal langs die i gewoonlik die tweede getal is, maak dit nie saak wanneer jy oplos nie. Oefen dit met die volgende koëffisiënte:
 = (1, 6)
= (1, 6) = (2, -1)
= (2, -1) = (-8, 6)
= (-8, 6)
3. Verwyder die absolute waardesimbole uit die vergelyking. Jy het nou net die koëffisiënte nodig. Onthou dat jy die afstand van die vergelyking vanaf nul bepaal. Aangesien jy die afstandsformule in die volgende stap gaan gebruik, is dit dieselfde as om die absolute waarde te bepaal.

4. Vierkant beide koëffisiënte. Om die afstand te bepaal, gebruik jy die afstandformule, ook bekend as  . So as `n eerste stap moet jy beide koëffisiënte van die komplekse vergelyking vierkantig maak. Ons gaan voort met die voorbeeld:
. So as `n eerste stap moet jy beide koëffisiënte van die komplekse vergelyking vierkantig maak. Ons gaan voort met die voorbeeld:  :
:
 . So as `n eerste stap moet jy beide koëffisiënte van die komplekse vergelyking vierkantig maak. Ons gaan voort met die voorbeeld:
. So as `n eerste stap moet jy beide koëffisiënte van die komplekse vergelyking vierkantig maak. Ons gaan voort met die voorbeeld:  :
:


5. Plaas die produk van die getalle onder die radikaal. Die radikale teken dui aan dat jy die vierkantswortel van die getal daaronder aftrek. Tel nou eers die getalle bymekaar, sonder om iets aan die radikale teken te doen.




6. Neem die vierkantswortel vir jou finale antwoord. Jy hoef net die vergelyking vir die finale antwoord te vereenvoudig. Dit is die afstand vanaf jou `punt` op `n denkbeeldige getallelyn tot by die nulpunt. As daar geen vierkantswortel is nie, laat net die antwoord van die laaste stap onder die radikale teken - dit is `n korrekte antwoord.





7. Probeer `n paar oefenoefeninge. Klik met jou muis direk agter die vrae om die antwoorde in wit te sien.
 = √37
= √37 = √5
= √5 = 10
= 10Wenke
- As jy `n veranderlike binne `n absolute waarde het, kan jy nie die absolute waardetekens met hierdie metode verwyder nie, want as die waarde van die veranderlike negatief is, dan sal die absolute waarde dit positief maak.
- As jy `n uitdrukking binne `n absolute waarde het, vereenvoudig die uitdrukking voordat jy die absolute waarde daarvan bepaal.
- Wanneer `n positiewe getal binne die absolute waardemerkers is, is die antwoord altyd daardie getal.
- Jy benodig `n ander metode om absolute waardevergelykings met `n x en y op te los, alhoewel die teorie agter die absolute waarde as basis gebruik word.
- `n Absolute waarde kan nooit `n negatiewe getal wees nie, so as jy iets sien soos | 2 - 4x| = -7, dan weet jy hierdie vergelyking is onwaar sonder om dit op te los.
Artikels oor die onderwerp "Bereken die absolute waarde van 'n getal"
Оцените, пожалуйста статью
Gewilde