Hoe om die aantal diagonale in 'n veelhoek te bepaal: 11 stappe (met prente)

Inhoud

Trappe
- Metode 1 van 2: Teken die hoeklyne
- Metode 2 van 2: Gebruik die formule vir die diagonaal

Om diagonale in `n veelhoek te vind is `n noodsaaklike vaardigheid om in wiskunde te vorder. Dit lyk dalk aanvanklik moeilik, maar is redelik maklik sodra jy die basiese formule leer. `n Diagonaal is enige segment getrek tussen hoekpunte van `n veelhoek wat nie die sye van daardie veelhoek bevat nie. `n Veelhoek is enige vorm wat meer as drie sye het. Deur `n baie eenvoudige formule te gebruik, kan jy die aantal diagonale in enige veelhoek bereken, of dit vier sye of 4000 sye het.

Trappe

Metode 1 van 2: Teken die hoeklyne

Prent getiteld Vind hoeveel diagonale is in `n veelhoek Stap 1

1. Ken die name van die verskillende veelhoeke. Jy sal dalk eers moet bepaal hoeveel sye die veelhoek het. Elke veelhoek het `n voorvoegsel wat die aantal sye aandui. Hier is die name van veelhoeke tot twintig kante:

Vierhoek/Tetragoon: 4 kante
Vyfhoek/vyfhoek: 5 kante
Seshoek/Heksagon: 6 kante
Seshoek: 7 kante
Octagon/Ocagon: 8 kante
Nonagoon/Enneagon: 9 kante
Dekagon: 10 kante
Hendecagon: 11 kante
Dodekagon: 12 kante
Triskaidecagon: 13 kante
Tetradekagon: 14 kante
Pentadekagon: 15 kante
Seshoek: 16 kante
Heptadekagon: 17 kante
Oktadekagon: 18 kante
Enneadekagon: 19 kante
Ikonsoon: 20 kante
Let daarop dat `n driehoek geen hoeklyne het nie.

Prent getiteld Vind hoeveel diagonale is in `n veelhoek Stap 2

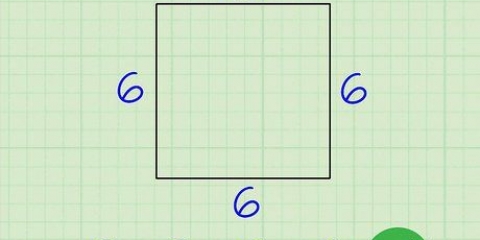
2. Teken die veelhoek. As jy wil weet hoeveel hoeklyne daar in `n vierkant is, begin jy deur die vierkant te teken. Die maklikste manier om diagonale te vind en te tel, is om die veelhoek simmetries te teken, waar elke sy dieselfde lengte het. Dit is belangrik om daarop te let dat selfs al is die veelhoek nie simmetries nie, dit steeds dieselfde aantal diagonale het.

Om die veelhoek te teken, gebruik `n liniaal en teken elke kant ewe lank en verbind alle kante.

As jy nie seker is hoe die veelhoek lyk nie, soek prente aanlyn. Byvoorbeeld, `n stopteken is `n agthoek.

Prent getiteld Vind hoeveel diagonale is in `n veelhoek Stap 3

3. Teken die hoeklyne. `n Diagonaal is `n segment wat van een hoek van die vorm na `n ander getrek word, die sye van die veelhoek uitgesluit. Gebruik `n liniaal om `n diagonaal na enige ander beskikbare hoekpunt te trek.

Vir `n vierkant, trek `n lyn van die onderste linkerhoek na die regter boonste hoek en `n ander lyn van die onderste regterhoek na die boonste linkerhoek.

Teken hoeklyne in verskillende kleure om dit makliker te maak om te tel.

Let daarop dat hierdie metode baie moeiliker word met veelhoeke met meer as tien sye.

Prent getiteld Vind hoeveel diagonale is in `n veelhoek Stap 4

4. Tel die hoeklyne. Daar is twee opsies om hoeklyne te tel: jy kan hulle tel wanneer jy die hoeklyne teken of wanneer hulle geteken word. Wanneer elke diagonaal getel word, skryf `n klein getal bokant die diagonaal om aan te dui dat dit getel is. Dit is maklik om te verdwaal terwyl jy tel wanneer baie hoeklyne inmekaar vleg.

Vir die vierkant is daar twee hoeklyne: een diagonaal vir elke twee hoekpunte.

’n Seshoek het nege hoeklyne: daar is drie hoeklyne vir elke drie hoekpunte.

’n Septigon het 14 diagonale. Anderkant die sewehoek word dit moeiliker om die hoeklyne te tel omdat daar so baie hoeklyne is.

Prent getiteld Vind hoeveel diagonale is in `n veelhoek Stap 5

5. Wees versigtig om nie jou hoeklyne meer as een keer te tel nie. Elke hoekpunt kan veelvuldige hoeklyne hê, maar dit beteken nie dat die aantal hoeklyne gelyk is aan die aantal hoekpunte maal die aantal hoeklyne nie. Wanneer jy die hoeklyne tel, maak seker dat jy elke hoeklyn net een keer tel.

Byvoorbeeld, `n vyfhoek (vyf sye) het net vyf hoeklyne. Elke hoekpunt het twee hoeklyne, so as jy elke hoeklyn van elke hoekpunt twee keer tel, sou jy dink daar is 10 hoeklyne. Dit is verkeerd, want jy het elke diagonaal twee keer getel!

Prent getiteld Vind hoeveel diagonale is in `n veelhoek Stap 6

6. Oefen met `n paar voorbeelde. Teken `n paar ander veelhoeke en tel die aantal hoeklyne. Die veelhoek hoef nie simmetries te wees vir hierdie metode om te werk nie. In die geval van `n konkawe veelhoek moet jy dalk `n paar diagonale buite die werklike veelhoek teken.

’n Seshoek of seshoek het 9 diagonale.

’n Septigon het 14 diagonale.

Metode 2 van 2: Gebruik die formule vir die diagonaal

Prent getiteld Vind hoeveel diagonale is in `n veelhoek Stap 7

1. Definieer die formule. Die formule om die aantal hoeklyne van `n veelhoek te vind is n(n-3)/2 waar `n` gelyk is aan die aantal sye van die veelhoek. Deur die distribusie-eienskap te gebruik, kan dit herskryf word as (n - 3n)/2. Jy kan albei maniere daarna kyk, albei vergelykings is identies.

Hierdie vergelyking kan gebruik word om die aantal hoeklyne van enige veelhoek te vind.
Let daarop dat die driehoek `n uitsondering op hierdie reël is. Weens die vorm van die driehoek het dit geen diagonale nie.

Prent getiteld Vind hoeveel diagonale is in `n veelhoek Stap 8

2. Bepaal die aantal sye van die veelhoek. Om hierdie formule te gebruik, moet jy die aantal sye van die veelhoek ken. Die aantal sye word in die naam van die veelhoek gegee, so jy hoef net te weet wat elke naam beteken. Hier is `n paar algemene voorvoegsels wat jy met veelhoeke kan teëkom:

Tetra (4), penta (5), hexa (6), hepta (7), octa (8), ennea (9), deca (10), hendeca (11), dodeca (12), trideca (13), tetradeca (14), pentadeca (15), ens.

Vir baie groot veelhoeke met baie sye kan jy net `n-goon` sien waar `n` die aantal sye is. Byvoorbeeld, `n 44-sydige veelhoek word geskryf as 44-goon.

Wanneer jy `n beeld van die veelhoek kry, kan jy eenvoudig die aantal sye tel.

Prent getiteld Vind hoeveel diagonale is in `n veelhoek Stap 9

3. Inkorporeer die aantal sye in die vergelyking. Sodra jy weet hoeveel sye die veelhoek het, moet jy net daardie getal in die vergelyking inreken en die vergelyking oplos. Waar jy ook al `n` in die vergelyking sien, word die aantal sye van die veelhoek vervang deur die aantal sye van die veelhoek.

Voorbeeld: `n Dodekagon het 12 kante.

Skryf die vergelyking: n(n-3)/2

Verwerk dit in die veranderlike: (12(12 - 3))/2

Prent getiteld Vind hoeveel diagonale is in `n veelhoek Stap 10

4. Los die vergelyking op. Laastens, los die vergelyking in die korrekte volgorde van bewerkings op. Begin deur die aftrekking op te los, dan die vermenigvuldiging en laastens die deling. Die laaste antwoord is die aantal hoeklyne wat die veelhoek het.

Byvoorbeeld: (12(12 - 3))/2

Trek af: (12*9)/2

Vermenigvuldig: (108)/2

Deel: 54

So `n dodecagon het 54 diagonale.

Prent getiteld Vind hoeveel diagonale is in `n veelhoek Stap 11

5. Oefen met meer voorbeelde. Hoe meer oefening jy met `n wiskunde konsep het, hoe beter kan jy dit gebruik. Om baie oefenvrae uit te werk, sal jou ook help om die formule te onthou ingeval jy dit nodig het vir `n vasvra, toets of eksamen. Onthou dat hierdie formule werk vir `n veelhoek met enige aantal sye groter as drie.

Seshoek (6 kante): n(n-3)/2=6(6-3)/2=6*3/2=18/2=9 hoeklyne.

Dekagon (10 sye): n(n-3)/2=10(10-3)/2=10*7/2=70/2=35 hoeklyne.

Ikosagon (20 kante): n(n-3)/2=20(20-3)/2=20*17/2=340/2=170 hoeklyne.

96-goon (96 kante): 96(96-3)/2=96*93/2=8928/2=4464 diagonale.