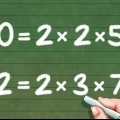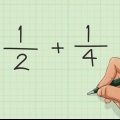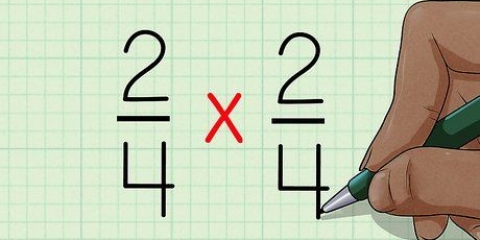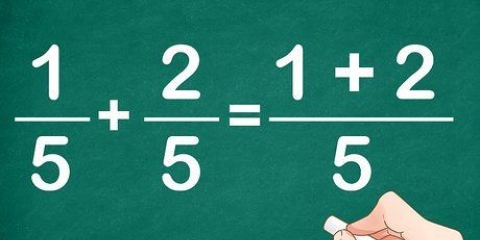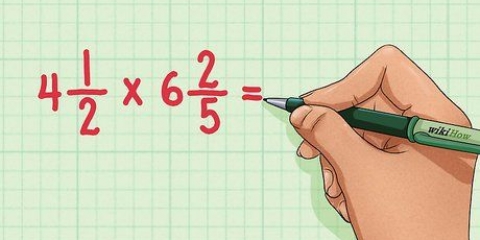Vind die kleinste gemene veelvoud van twee noemers

Inhoud

Trappe
Benodigdhede

Om breuke met verskillende noemers op te tel of af te trek. dit is nodig om eers die kleinste gemene veelvoud van hierdie twee getalle te vind. Dit is die kleinste veelvoud van enige noemer in `n vergelyking. Hier is `n paar verskillende metodes wat jy kan gebruik om die lcm te vind en dit te gebruik om breukprobleme op te los.

Trappe

Metode 1 van 4: Lys veelvoude

Prent getiteld Vind die minste gemene deler Stap 1

1. Lys die veelvoude van elke noemer. Elke lys moet bestaan uit die noemer van die breuk vermenigvuldig met 1, 2, 3, 4, ensovoorts.

Voorbeeld: 1/2 + 1/3 + 1/5
Veelvoude van 2: 2 *1=2; 2 *2=4; 2 *3=6; 2 *4=8; 2 *5=10; 2 *6=12; 2 *7=14; ens.
Veelvoude van 3: 3 *1=3; 3 *2=6; 3 *3=9; 3 *4=12; 3 *5=15; 3 *6=18; 3 *7=21; ens.
Veelvoude van 5: 5 *1=5; 5 *2=10; 5 *3=15; 5 *4=20; 5 *5=25; 5 *6=30; 5 *7=35; ens.

Prent getiteld Vind die minste gemene deler Stap 2

2. Vind die kleinste gemene veelvoud. Skandeer deur elke lys en merk enige gemeenskaplike veelvoud van beide noemers uit. Nadat u die gemene veelvoude bepaal het, bepaal watter die kleinste is.

Let daarop dat as daar tans geen gemene veelvoud is nie, moet jy voortgaan totdat jy wel `n veelvoud kry wat geldig is vir beide noemers.

Voorbeeld: 2 *15=30; 3 *10=30; 5 *6=30

Die kgv=30

Prent getiteld Vind die minste gemene deler Stap 3

3. Herskryf die oorspronklike probleem. Om elke breuk in hierdie som te skryf sodat dit dieselfde waarde as die oorspronklike probleem het, is dit nodig om die breuk se teller en noemer te vermenigvuldig met die toepaslike waarde, wat ooreenstem met die gemene veelvoud gevind.

Voorbeeld: 15 *(1/2); 10 *(1/3); 6 *(1/5)

Nuwe som: 15/30 + 10/30 + 6/30

Prent getiteld Vind die minste gemene deler Stap 4

4. Los op. Nadat jy die LCF gevind het en die breuke gewysig is, behoort jy hierdie probleem sonder enige probleme op te los.

Voorbeeld: 15/30 + 10/30 + 6/30=31/30=1 1/30

Metode 2 van 4: Gebruik die grootste gemene deler

Prent getiteld Vind die minste gemene deler Stap 5

1. Vind die grootste gemene deler van elke noemer. Vind uit of daar `n grootste gemene deler vir beide noemers is deur uit te vind watter getalle deur die noemers deelbaar is.

Voorbeeld: 3/8 + 5/12
Faktore van 8: 1, 2, 4, 8
Faktore van 12: 1, 2, 3, 4, 6, 12

Prent getiteld Vind die minste gemene deler Stap 6

2. Identifiseer die grootste gemene deler tussen beide noemers. Omkring alle GCD`s nadat jy die faktore van elke noemer gevind het. Die grootste van die GCD`s is die grootste gemene deler wat jy kan gebruik om die probleem verder op te los.

In ons voorbeeld deel 8 en 12 die noemer 1, 2 en 4.

Die grootste gemene deler is 4.

3. Vermenigvuldig die noemers saam. Gaan na die volgende stap deur die twee noemers saam te vermenigvuldig.

Voorbeeld: 8 *12=96

Prent getiteld Vind die minste gemene deler Stap 7

4. Deel deur die gcd. Nadat jy die produk van beide noemers gevind het, deel dit deur die voorheen gevind gcd. Die resultaat van hierdie deling is jou kleinste gemene veelvoud.

Voorbeeld: 96 / 4=24

Prent getiteld Vind die minste gemene deler Stap 8

5. Herskryf die oorspronklike probleem. Herskryf die tellers deur hulle te vermenigvuldig met dieselfde getal wat dit geneem het om die ooreenstemmende noemers gelyk te maak aan die lcg. Vind die faktor vir elke breuk deur die lcm deur die oorspronklike noemer te deel.

Voorbeeld: 24 / 8=3; 24/12=2

3 *(3/8)=9/24; 2 *(5/12)=10/24

24/9 + 24/10

Prent getiteld Vind die minste gemene deler Stap 9

6. Los die probleem op. Met die kgv gevind behoort dit nou moontlik te wees om op te tel en af te trek sonder enige probleme.

Voorbeeld: 9/24 + 10/24=19/24

Metode 3 van 4: Faktorering van breuke in priemfaktore

Prent getiteld Vind die minste gemene deler Stap 10

1. Verdeel die noemers in priemgetalle. Verdeel elke noemer in `n reeks priemgetalle. Onthou dat priemgetalle daardie getalle is wat nie deur enige ander getal behalwe 1 en homself gedeel kan word nie.

Voorbeeld: 1/4 + 1/5 + 1/12
Die priemfaktore van 4: 2 *2
Die priemfaktore van 5: 5
Die priemfaktore van 12: 2 *2 *3

Prent getiteld Vind die minste gemene deler Stap 11

2. Tel die aantal kere wat elke priemgetal in die stel priemfaktore voorkom. Turf die aantal kere wat elke priemgetal in die priemfaktore van elke noemer voorkom.

Voorbeeld: Daar is twee 2-en in 4; nul 2-en in 5; twee 2-en in 12

Daar is nul 3-en in 4 en 5; a 3 in 12

Daar is nul 5-en in 4 en 12; a 5 in 5

Prent getiteld Vind die minste gemene deler Stap 12

3. Neem die grootste getal vir enige priemgetal. Let op hoeveel keer jy elke priemgetal gebruik het.

Voorbeeld: Die grootste getal vir 2 is twee; die grootste getal vir 3 is `n; die grootste getal vir 5 is `n.

Prent getiteld Vind die minste gemene deler Stap 13

4. Skryf dit hieronder as `n voorbeeld.

Voorbeeld: 2, 2, 3, 5

Prent getiteld Vind die minste gemene deler Stap 14

5. Vermenigvuldig alle priemgetalle so. Vermenigvuldig die priemgetalle van die vorige reeks. Die produk van hierdie getalle is gelyk aan die lcm van die oorspronklike probleem.

Voorbeeld: 2 *2 *3 *5=60

kgf=60

Prent getiteld Vind die minste gemene deler Stap 15

6. Herskryf die oorspronklike probleem. Verdeel die LCF deur die oorspronklike noemer. Vermenigvuldig elke teller met dieselfde getal wat nodig is om die ooreenstemmende noemer die LCF te maak.

Voorbeeld: 60/4=15; 60/5=12; 60/12=5

15 *(1/4)=15/60; 12 *(1/5)=12/60; 5 *(1/12)=5/60

15/60 + 12/60 + 5/60

Prent getiteld Vind die minste gemene deler Stap 16

7. Los op. Met die LCF gevind en soortgelyke noemers het dit maklik geword om die breuke op te tel en af te trek soos gewoonlik.

Voorbeeld: 15/60 + 12/60 + 5/60=32/60=8/15

Metode 4 van 4: Werk met heelgetalle en gemengde getalle

Prent getiteld Vind die minste gemene deler Stap 17

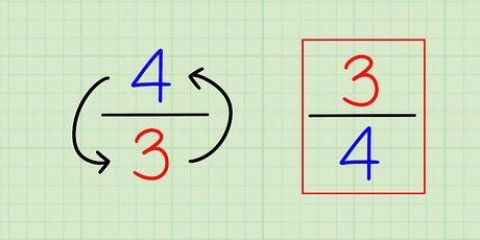
1. Skakel enige heelgetal en gemengde getal om na `n onbehoorlike breuk. Skakel gemengde getalle om na onbehoorlike breuke deur die heelgetal voor die breuk met die noemer te vermenigvuldig en die teller by die produk te voeg. Skakel `n heelgetal om na `n onbehoorlike breuk deur dit as `n teller in `n breuk met die noemer `1` te plaas.

Voorbeeld: 8 + 2 1/4 + 2/3
8=8/1
2 1/4; 2 *4 + 1=8 + 1=9; 9/4
Hergeskrewe opdrag: 8/1 + 9/4 + 2/3

Prent getiteld Vind die minste gemene deler Stap 18

2. Vind die kleinste gemene veelvoud van die noemers. Pas een van die metodes toe om die LCF van `n gewone breuk te vind, soos hierbo beskryf. Let daarop dat ons in hierdie voorbeeld die `Lysveelvoude`-metode gebruik, `n lys van veelvoude vir elke noemer skep en die lcm hieruit aflei.

Let daarop dat jy nie veelvoude van hoef te lys nie 1 want elke getal is `n veelvoud van 1.

Voorbeeld: 4 *1=4; 4 *2=8; 4 *3=12; 4 *4=16; ens.

3 *1=3; 3 *2=6; 3 *3=9; 3 *4=12; ens.

Die kgv=12

Prent getiteld Vind die minste gemene deler Stap 19

3. Herskryf die oorspronklike probleem. In plaas daarvan om net die noemer te vermenigvuldig, is dit nodig om ook die teller te vermenigvuldig met die getal wat nodig is om die noemer `n lcg te maak.

Voorbeeld: 12 *(8/1)=96/12; 3 *(9/4)=27/12; 4 *(2/3)=8/12

96/12 + 27/12 + 8/12

Prent getiteld Vind die minste gemene deler Stap 20

4. Los die probleem op. Nadat die breuk aangepas is en die lcm in die noemer gevind is, behoort dit maklik te wees om die breuke op te tel en af te trek sonder enige probleme.

Voorbeeld: 96/12 + 27/12 + 8/12=131/12=10 11/12