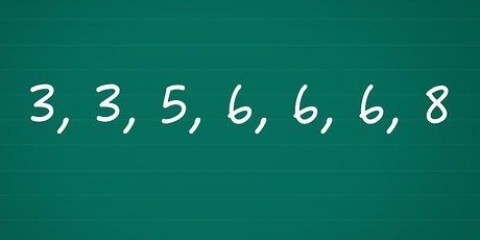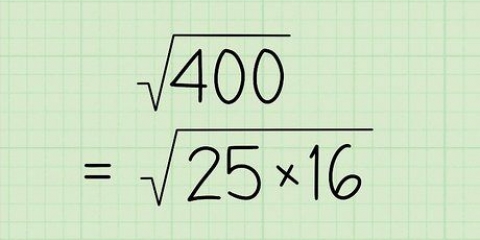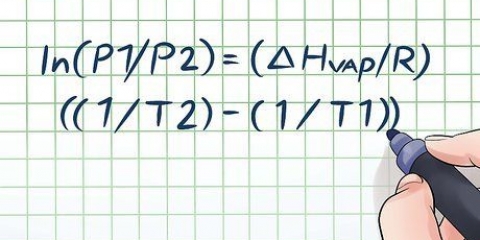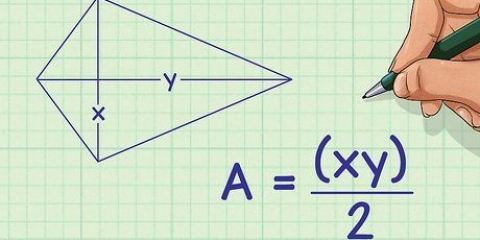Berekening van die omvang: 4 stappe (met prente)

Inhoud

Trappe
Wenke

Die `reeks` in die statistiek verteenwoordig die verskil tussen die hoogste en laagste waardes in `n datastel. Die reeks wys hoe verspreid die waardes in `n reeks is. As die reeks wyd is, is die waardes in die reeks ver uitmekaar; as die reeks klein is, dan is die waardes naby aan mekaar. As jy wil weet hoe om die strooiwydte te bereken, hoef jy net hierdie stappe te volg.

Trappe

1. Lys die elemente in jou datastel. Om die omvang van `n stel te vind, moet jy al die elemente van die stel in lyn bring sodat jy die hoogste en laagste getalle kan vind. Skryf al die elemente neer. Die nommers in hierdie stel is: 14, 19, 20, 24, 25 en 28.

Dit is makliker om die hoogste en laagste getalle in die stel te vind as jy die getalle in stygende volgorde plaas. In hierdie voorbeeld is die stel soos volg gerangskik: 14, 19, 20, 24, 24, 25, 28.
Die organisering van die datastel kan jou ook help om ander berekeninge te doen, soos om die modus, gemiddelde of mediaan van die stel te vind.

2. Vind die hoogste en laagste getalle in die stel. In hierdie geval is die laagste getal in die stel 14, en die hoogste getal is 28.

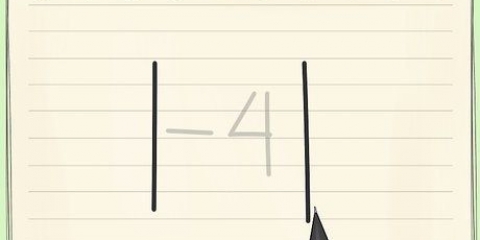
3. Trek die kleinste getal in jou datastel van die grootste getal af. Noudat jy die kleinste en grootste getal in die stel gevind het, hoef jy dit net af te trek. Trek 14 af van 28 (28 - 14) en jy kry 14, die verspreidingswydte van die stel.

4. Benoem die verspreidingswydte. Sodra jy die verspreiding gevind het, merk dit duidelik. Dit voorkom verwarring met enige ander statistiese berekeninge wat jy dalk vir die stel moet maak, soos om die mediaan, modus of gemiddelde te vind.

Wenke

Die mediaan van `n statistiese datastel verteenwoordig die `middel` van die datastel in terme van verspreiding en nie die omvang van die data. Dus, hoewel dit aanloklik is om te aanvaar dat die mediaan van `n gegewe datastel die reeks is gedeel deur 2 - of halfpad tussen die uiterstes van die reeks - is dit gewoonlik nie die geval nie. Om die korrekte mediaan te vind moet jy eers die data-elemente in volgorde plaas, en dan die element in die middel van die lys vind. Daardie element is die mediaan. Byvoorbeeld, as jy `n lys met 29 elemente het, is die 15de element ewe ver van beide die bo- en onderkant van die geordende lys. Die 15de element is dus die mediaan, ongeag hoe daardie waarde met die reeks verband hou.
Jy kan ook `verspreiding` in `n algebraïese konteks verstaan, waar dit gewoonlik `reeks` genoem word. Om dit te verstaan moet jy eers `n idee kry van die konsep van die algebraïese funksie, of volgorde van bewerkings op `n gegewe getal. Omdat die funksie se bewerkings op enige getal uitgevoer kan word - selfs `n onbekende getal - word die getal voorgestel deur `n letterveranderlike, gewoonlik "x". Die domein is die stel van alle moontlike invoerwaardes wat u met hierdie onbekende nommer kan vervang. Die omvang van die funksie is die stel van alle moontlike resultate wat u kan kry as u een van die domeinwaardes invoer en al die bewerkings van die funksie uitvoer. Ongelukkig is daar nie een manier om die omvang van `n funksie te bereken nie. Soms kan die grafiek van die funksie of die berekening van veelvuldige waardes `n duidelike patroon toon. Jy kan ook wat jy weet oor die domein van die funksie gebruik om moontlike uitvoerwaardes uit te sluit, of om die datastel wat die omvang aandui te beperk.