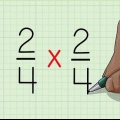(/2) = /2 × /2 of (/2). Om elke getal te kwadraat gee (/4). 
Die teller bly bo-op die breuk en die noemer bly aan die onderkant. Byvoorbeeld: (/2) = (/2 x 2) = (/4). 
Om dit na `n gemengde getal om te skakel, deel 25 deur 4. Dit is 6 (6 x 4 = 24), met `n res van 1. Daarom is die gemengde getal 6/4. 

Byvoorbeeld: (-/4) = (–/4) x (–/4) 
Byvoorbeeld: (-2) x (-8) = (+16) 
Gaan voort met die voorbeeld, die resulterende breuk sal `n positiewe getal wees. (–/4) x (–/4) = (+/16) Die gebruik is om die plusteken van positiewe getalle weg te laat. 
Byvoorbeeld: (/16) het `n gemeenskaplike faktor van vier. Deel die breuk deur 4: 4/4 = 1, 16/4= 4 Herskryf die vereenvoudigde breuk: (/4) 

Byvoorbeeld: 16 × (/16) Vier die hakies en skakel die gemeenskaplike faktor van 16 uit: 16 * /16 * /16 Aangesien jy hier te doen het met `n 16 as `n heelgetal en twee keer `n 16 in die noemer, kan jy een van hulle uitskakel. Herskryf die vereenvoudigde vergelyking: 12 × /16 vereenvoudig /16 deur te deel deur 4: /4 Vermenigvuldig: 12 × /4 = 36/4 Deel: 36/4 = 9 
Byvoorbeeld: 16 * (/16) Herskryf met die kwadraat teller en noemer: 16 * (/16) Trek die eksponent in die noemer af: 16 * /16 Stel jou die eerste 16 voor as `n eksponent van 1:16. Deur die reëls vir die aftrekking van magte/eksponente te gebruik, trek jy die eksponente van mekaar af. 16/16, gee 16 = 16 of 1/16. Nou gaan jy voort met /16 Herskryf en vereenvoudig die breuk: /16 =* /4. Vereenvoudig: 12 × /4 = 36/4 Deel: 36/4 = 9
Kwadrateer breuke
Inhoud
Om breuke te kwadraat is een van die eenvoudigste bewerkings wat jy op breuke kan uitvoer. Dit is baie soortgelyk aan kwadratering van heelgetalle deurdat jy net beide die teller en noemer met hulself kan vermenigvuldig. Daar is sommige gevalle waar die vereenvoudiging van die breuk voor kwadratering die prosedure makliker maak. As jy nog nie hierdie vaardigheid aangeleer het nie, bied hierdie artikel `n kort oorsig om jou begrip te verbeter.
Trappe
Deel 1 van 3: Kwadratering van breuke

1. Verstaan hoe om heelgetalle te vier. Wanneer jy `n getal sien wat tot die tweede mag verhoog word, weet jy om die getal te kwadraat. Dit is dieselfde as om die getal met homself te vermenigvuldig. Byvoorbeeld:
- 5 = 5 × 5 = 25

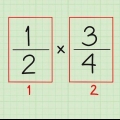
2. Besef jy daardie kwadraatbreuke werk op dieselfde manier. Om `n breuk te kwadraat, vermenigvuldig die breuk met homself. Nog `n manier om hieroor te dink, is om die teller met homself en die noemer met homself te vermenigvuldig. Byvoorbeeld:

3. Vermenigvuldig die teller met homself en die noemer met homself. Die werklike volgorde waarin jy hierdie getalle met hulself vermenigvuldig, maak nie saak nie, solank jy albei getalle vierkantig maak. Om dinge eenvoudig te hou, begin met die teller: vermenigvuldig dit net met homself. Vermenigvuldig dan die noemer met homself.

4.Vereenvoudig die breuk om dit af te sluit. Wanneer ons met breuke handel, is die laaste stap altyd om die breuk tot sy eenvoudigste vorm te vereenvoudig of `n onbehoorlike breuk in `n gemengde getal om te skakel. Ons voorbeeld, /4 is `n onbehoorlike breuk omdat die teller groter is as die noemer.
Deel 2 van 3: Kwadrateer breuke met negatiewe getalle

1. Soek `n minusteken voor die breuk. As jy met `n negatiewe breuk te doen het, is daar `n minusteken voor. Dit is wys om altyd hakies om `n negatiewe getal te sit sodat jy weet dat die minusteken na die getal verwys en nie bedoel is as `n minussom nie.
- Byvoorbeeld: (-/4)

2. Vermenigvuldig die breuk met homself. Kwadrateer die breuk soos jy normaalweg sou doen, deur die teller met homself te vermenigvuldig en dan die noemer met homself te vermenigvuldig. Jy kan ook net die breuk met homself vermenigvuldig.

3. Verstaan dat die vermenigvuldiging van twee negatiewe getalle saam `n positiewe getal maak. Wanneer `n minusteken teenwoordig is, word die hele breuk negatief. Wanneer jy die breuk vierkantig, vermenigvuldig jy twee negatiewe getalle. Wanneer twee negatiewe getalle met mekaar vermenigvuldig word, is die produk altyd positief.

4. Verwyder die minusteken na kwadratering. As jy die breuk gekwadraeer het, het jy twee negatiewe getalle vermenigvuldig. Dit beteken dat die kwadraatbreuk positief is. Moenie vergeet om die minusteken in die finale antwoord weg te laat nie.

5. Vereenvoudig die breuk so ver as moontlik. Die laaste stap om breukberekeninge te doen, is om te vereenvoudig. Onbehoorlike breuke moet eers na gemengde getalle vereenvoudig en dan verder vereenvoudig word.
Deel 3 van 3: Gebruik vereenvoudigings en kitsoplossings

1. Kyk of jy die breuk kan doenvereenvoudig voordat jy dit vierkantig maak. Dit is gewoonlik makliker om breuke te vereenvoudig voor kwadratering. Onthou, om `n breuk te vereenvoudig, behels dit om dit deur `n gemeenskaplike faktor te deel totdat 1 die enigste getal oor is wat deur beide die teller en die noemer gedeel kan word. Om eers `n breuk te vereenvoudig, beteken dat jy dit nie weer aan die einde hoef te vereenvoudig wanneer die getalle groter is nie.
- Byvoorbeeld: (/16)
- 12 en 16 kan albei deur 4 gedeel word. 12/4 = 3 en 16/4 = 4; dus kan jy/16 vereenvoudig tot /4.
- Nou kan jy die breuk doen /4 vierkantig te maak.
- (/4) = /16, wat jy nie meer kan vereenvoudig nie.
- Om dit te bewys, vier ons die oorspronklike breuk sonder om te vereenvoudig:
- (/16) = (/16x16) = (/256)
- (/256) het `n gemeenskaplike faktor van 16. Deur beide die teller en noemer deur 16 te deel, vereenvoudig die breuk tot (/16), dieselfde breuk wat ons gekry het deur eers te vereenvoudig.

2. Leer wanneer om op te hou om `n breuk te vereenvoudig. Het jy te doen met meer komplekse vergelykings, dan is dit dalk moontlik om een van die faktore uit te skakel. In so `n geval is dit dus geriefliker om te wag met die vereenvoudiging van die breuk. Deur `n ekstra faktor by die voorbeeld hierbo te voeg, maak dit duideliker.

3. Verstaan hoe om dit vinnig te doen met dieeksponent. Nog `n manier om dieselfde probleem op te los, is om eers die eksponent te vereenvoudig. Die resultaat sal dieselfde wees, slegs verkry deur `n ander roete.
Benodigdhede
- Papier of `n rekenaar
- Potlood/pen (indien papier gebruik word)
Artikels oor die onderwerp "Kwadrateer breuke"
Оцените, пожалуйста статью
Gewilde