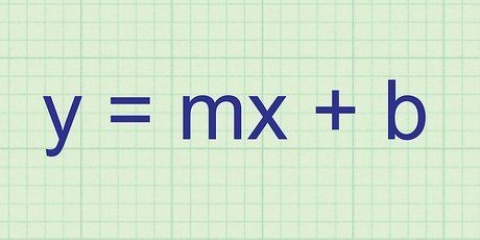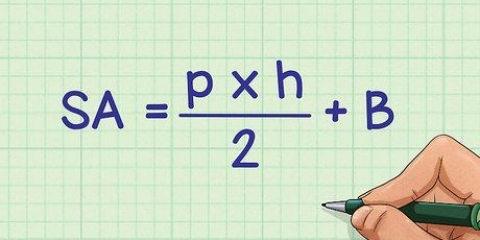Hoe om die lengte van die hipotenusa te bepaal

Inhoud

Trappe

Alle reghoekige driehoeke het `n regte hoek (van 90 grade), en die skuinssy is die kant teenoor daardie hoek. Die skuinssy is die langste sy van die driehoek, en is ook baie maklik om te vind met behulp van `n aantal verskillende metodes. Hierdie artikel sal jou leer hoe om die lengte van die skuinssy met behulp van die Pythagoras-stelling te bepaal, mits jy weet wat die lengte van die ander twee sye van die driehoek is. Dan sal jy leer hoe om die skuinssy van `n paar spesiale reghoekige driehoeke te bereken wat jy dikwels in toetse sal teëkom. En uiteindelik sal jy leer hoe om die lengte van die skuinssy met behulp van die Sinus-reël te bereken, wanneer slegs die lengte van een van die sye bekend is en die grootte van een van die hoeke.

Trappe

Metode 1 van 3: Gebruik die Pythagoras-stelling

Prent getiteld Vind die lengte van die hipotenusa Stap 1

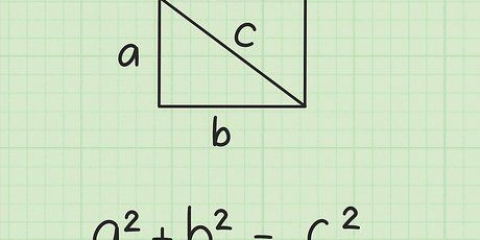
1. Leer Pythagoras se Stelling. Die Pythagoras-stelling beskryf die verwantskap tussen die sye van `n reghoekige driehoek. Dit stel dat vir `n arbitrêre reghoekige driehoek met sye a en b, en skuinssy van lengte c, ons het a + b = c.

Prent getiteld Vind die lengte van die hipotenusa Stap 2

2. Maak seker jou driehoek is `n reghoekige driehoek.Die Pythagoras-stelling werk net vir reghoekige driehoeke, en per definisie kan slegs `n reghoekige driehoek `n skuinssy hê.As jou driehoek `n hoek van presies 90 grade bevat, dan is dit `n reghoekige driehoek en jy kan voortgaan.

Regte hoeke word dikwels in handboeke en toetse aangedui met `n klein vierkant in die regterhoek. Hierdie spesiale merk beteken "90 grade."

Prent getiteld Vind die lengte van die hipotenusa Stap 3

3. Ken veranderlikes a, b en c toe aan die sye van jou driehoek.Die veranderlike "c" word altyd aan die skuinssy toegewys, dit wil sê die langste sy.Kies een van die ander kante vir die a, en noem die oorblywende kant b (dit maak nie saak watter een nie, die wiskunde bly dieselfde).Verwerk dan die lengtes van a en b in die formule, soos getoon in die volgende voorbeeld:

As jou driehoek sye van 3 en 4 het, en jy het letters aan daardie sye toegewys sodat a = 3 en b = 4, werk jy die vergelyking uit soos: 3 + 4 = c.

Prent getiteld Vind die lengte van die hipotenuse Stap 4

4. Bepaal die vierkante van a en b.Om die kwadraat van `n getal te vind, vermenigvuldig net daardie getal met homself, dus a = a x a. Vind die vierkante van beide a en b, en inkorporeer hulle in die formule.

As a = 3, a = 3 x 3, of 9.As b = 4, dan is b = 4 x 4, of 16.

Wanneer jy daardie waardes in jou vergelyking inreken, moet dit nou soos volg lyk: 9 + 16 = c.

Prent getiteld Vind die lengte van die hipotenusa Stap 5

5. Tel die waardes vana en b saam aan. Faktoreer dit in jou vergelyking, en dit gee jou die waarde van c. Nou is daar net een stap om te gaan, en jy het die skuinssy bepaal!

In ons voorbeeld, 9 + 16 = 25, neem dan kennis 25 = c.

Prent getiteld Vind die lengte van die hipotenusa Stap 6

6. Bepaal die vierkantswortel van c. Gebruik die vierkantswortelfunksie op jou sakrekenaar (of vermenigvuldigingstabelle, as jy dit uit die kop ken) om die vierkantswortel van c te vind. Die antwoord is die lengte van jou skuinssy!

In ons voorbeeld, c = 25.Die vierkantswortel van 25 is 5 (5 x 5 = 25, Dus Sqrt(25) = 5).En dit beteken c = 5, die lengte van ons skuinssy!

Metode 2 van 3: Bepaling van die skuinssy van spesiale reghoekige driehoeke

Prent getiteld Vind die lengte van die hipotenusa Stap 7

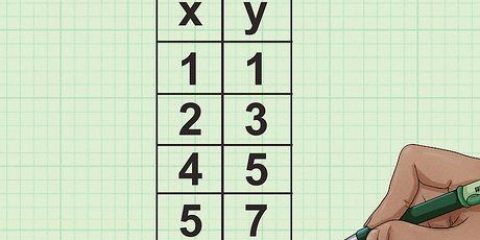
1. Leer om die driehoeke van `n Pythagorese drietal te herken. Die lengtes van die sye van `n Pythagorese triade is heelgetalle wat die Pythagoreaanse Stelling gehoorsaam. Jy sal gereeld hierdie spesiale driehoeke in meetkundehandboeke en in standaardtoetse soos die SAT en die GRE teëkom.In die besonder, as jy die eerste 2 Pythagorese driehoeke memoriseer, kan jy jouself baie tyd op daardie toetse bespaar omdat jy dadelik die skuinssy van enige van hierdie driehoeke ken deur net na die lengtes van die sye te kyk!

Die eerste Pythagorese trio is 3-4-5 (3 + 4 = 5, 9 + 16 = 25).Wanneer jy `n reghoekige driehoek met sye van lengte 3 en 4 sien, weet jy dadelik vir seker dat die skuinssy 5 sal wees sonder dat jy enige berekeninge hoef te doen.
Die verhouding van `n Pythagorese trippel bly dieselfde selfs wanneer die sye met `n ander getal vermenigvuldig word. Byvoorbeeld: `n reghoekige driehoek met sye 6 en 8 sal `n skuinssy van 10 (6 + 8 = 10, 36 + 64 = 100).Dieselfde geld vir9-12-15, selfs 1,5-2-2,5.Doen die berekeninge en jy sal sien!
Die tweede Pythagorese trio wat jy dikwels in toetse sal teëkom is 5-12-13 (5 + 12 = 13, 25 + 144 = 169).Wees ook op die uitkyk vir die meervoude daarvan, soos 10-24-26 en 2,5-6-6,5.

Prent getiteld Vind die lengte van die hipotenusa Stap 8

2. Leer die verhouding van die sye van `n reghoekige driehoek met hoeke 45-45-90. `n Regte driehoek van 45-45-90 het hoeke van 45, 45 en 90 grade, en word ook `n gelykbenige reghoekige driehoek genoem. Hierdie een word gereeld op standaardtoetse gevind, en is `n baie maklike driehoek om op te los. Die verhouding van die sye van hierdie driehoek is 1:1:Sqrt(2), wat beteken dat die lengte van die bene gelyk is, en die lengte van die skuinssy is dan bloot die lengte van die bene vermenigvuldig met die vierkantswortel van twee.

Jy bereken die skuinssy van hierdie driehoek gebaseer op die lengte van een van die bene, en vermenigvuldig sy lengte met Sqrt(2).

Dit is nuttig om hierdie verhouding te ken, veral as jou toets- of huiswerkprobleme jou die lengtes van sye in die vorm van veranderlikes in plaas van heelgetalle gee.

Prent getiteld Vind die lengte van die hipotenusa Stap 9

3. Leer die proporsies van `n reghoekige 30-60-90 driehoek. Hierdie driehoek het hoeke van 30, 60 en 90 grade en kan gemaak word deur `n gelyksydige driehoek in die helfte te deel. Die sye van die regte driehoek 30-60-90 het altyd die verhouding 1:Sqrt(3):2, of x:Sqrt(3)x:2x.As die lengte van een been van die regte 30-60-90 driehoek gegee word en gevra word om die skuinssy te bepaal, is dit baie maklik om te doen:

Gegewe die lengte van die kortste been (die een teenoor die 30 grade hoek), vermenigvuldig die lengte van daardie been met 2 om die lengte van die skuinssy te kry. Byvoorbeeld, as die lengte van die kortste been 4 is, dan weet jy dat die skuinssy 8 moet wees.

As jy die lengte van die langer been ken (teenoor die 60 grade hoek), vermenigvuldig daardie lengte met2/Sqrt(3) om die lengte van die skuinssy te vind.Byvoorbeeld, as die lengte van die kortste been 4 is, dan weet jy dat die skuinssy 4,62 moet wees.

Metode 3 van 3: Berekening van die skuinssy met die sinusreël

Prent getiteld Vind die lengte van die hipotenusa Stap 10

1. Verstaan wat die "Sinus" beteken. Die terme "sinus," "kosinus" en "raaklyn" almal verwys na sekere verhoudings tussen die hoeke en/of sye van `n reghoekige driehoek.In `n reghoekige driehoek is die is sinus van `n hoek gedefinieer as die lengte van die sy oorkant die hoek gedeel deur die skuinssy van die driehoek. Die afkorting vir sinus soos dit op jou sakrekenaar verskyn is sonde.

Prent getiteld Vind die lengte van die hipotenuse Stap 11

2. Leer hoe om die sinus te bereken. Selfs `n eenvoudige wetenskaplike sakrekenaar het `n sinusfunksie. Kyk na die sleutel gemerk sonde.Om die sinus van `n hoek te vind sal jy gewoonlik op die druk sonde-sleutel en sleutel dan die hoek in grade in.Op sommige sakrekenaars moet jy egter eers die hoek in grade invoer en dan die druk sonde-druk knoppie. Jy sal met jou sakrekenaar moet eksperimenteer of in die handleiding moet kyk om te bepaal watter een dit is.

Om die sinus van `n 80-grade hoek te vind, sal jy sonde 80 moet tik gevolg deur die gelykheidsteken of Enter, of80 sonde. (Die antwoord is -0,9939.)

Jy kan ook soek vir "sonde sakrekenaar" met jou blaaier vir `n paar maklik-om-te gebruik sakrekenaars sodat jy nie hoef te raai nie.

Prent getiteld Vind die lengte van die hipotenusa Stap 12

3. Leer die sinusreël.Die sinusreël is `n nuttige hulpmiddel om driehoekprobleme op te los. Jy kan dit hoofsaaklik gebruik om die skuinssy van `n reghoekige driehoek te vind, as jy die lengte van een sy ken, en een van sy hoeke anders as die regte hoek. Vir enige driehoek met sye a, b en c en die hoeke a, B en C, die sinusreël bepaal dat `n / sonde a = b / sonde B = c / sonde C.

Die sinusreël kan in werklikheid gebruik word om op te los elk driehoek, maar slegs `n reghoekige driehoek sal `n skuinssy hê.

Prent getiteld Vind die lengte van die hipotenusa Stap 13

4. Ken die veranderlikes a, b en c toe aan die sye van jou driehoek. Die skuinssy (die langste sy) moet altyd die "c" is. Vir eenvoud, benoem die kant van bekende lengte as "a" en ander "b". Ken dan die veranderlikes A, B en C toe aan die hoeke van die driehoek. Die regte hoek oorkant die skuinssy word dan "C".Die hoek oorkant "a" is hoek "a" en die hoek teenoorgestelde kant "b" is "B".

Prent getiteld Vind die lengte van die hipotenusa Stap 14

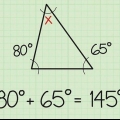
5. Bereken die derde hoek. Omdat dit `n regte hoek is, weet jy dit reeds C = 90 grade en jy weet ook watter hoek a of B is. Aangesien die som van alle hoeke in `n driehoek altyd gelyk moet wees aan 180 grade, is dit maklik om die derde hoek te bereken deur die formule te gebruik: 180 – (90 + A) = B. Jy kan ook hierdie vergelyking omkeer sodat 180 – (90 + B) = A.

Byvoorbeeld, as jy dit weet A = 40 grade, dan B = 180 – (90 + 40). Vereenvoudig dit tot B = 180 – 130 en jy kan dit vinnig aflei B = 50 grade.

Prent getiteld Vind die lengte van die hipotenusa Stap 15

6. Ondersoek jou driehoek.Op hierdie punt ken jy al die hoeke van die driehoek en die lengte van sy a. Nou is dit tyd om hierdie waardes in die sinusreël te verwerk, om die lengte van die ander twee sye te bereken.

Om voort te gaan met ons voorbeeld, kom ons sê dat die lengte van sy a = 10.Hoek C = 90 grade, hoek A = 40 grade, en hoek B = 50 grade.

Prent getiteld Vind die lengte van die hipotenusa Stap 16

7. Pas die sinusreël toe op jou driehoek.Ons hoef net ons getalle te verwerk en die volgende vergelyking op te los om die lengte van skuinssy c te vind: lengte van sy a / sonde A = lengte van sy c / sonde C.Dit lyk dalk nog ietwat intimiderend, maar die 90 grade sinus is `n konstante en is altyd gelyk aan 1!Ons vergelyking kan dus vereenvoudig word na: `n / sonde A = c / 1, of eenvoudiger `n / sonde A = c.

Prent getiteld Vind die lengte van die hipotenusa Stap 17

8. Verdeel die lengte van sya deur die sinus van hoek a om die lengte van die skuinssy te vind!Jy kan dit in twee afsonderlike stappe bereken, deur eers: sonde Bereken en skryf A en deel dan deur a. Of toets dit alles op een slag in jou sakrekenaar. As jy dit doen, moenie die hakies na die verdelingsteken vergeet nie.Sleutel byvoorbeeld in 10 / (sonde 40) of 10 / (40 sonde), afhangende van jou sakrekenaar.

Om van ons voorbeeld te begin, sien ons dit sonde 40 = 0,64278761.Om die waarde van c te vind, deel ons die lengte van a deur hierdie getal, en vind dit 10 / 0,64278761 = 15,6, die lengte van ons skuinssy!