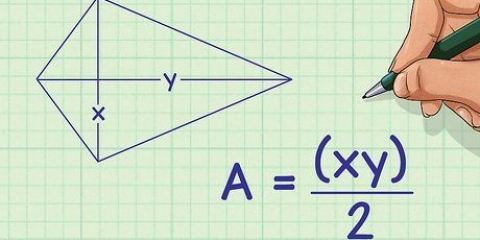Berekening van die oppervlakte van 'n ellips: 5 stappe (met prente)

Inhoud

Trappe
- Deel 1 van 2: Berekening van die oppervlakte
- Deel 2 van 2: Verstaan hoekom dit werk
Wenke

`n Ellips is `n tweedimensionele vorm wat jy dalk reeds uit die meetkundeklas ken, wat soos `n langwerpige sirkel lyk. Om die oppervlakte van `n ellips te bereken is maklik as jy die lengte van die grootste radius en die kleinste radius ken.

Trappe

Deel 1 van 2: Berekening van die oppervlakte

Prent getiteld Bereken die oppervlakte van `n ellips Stap 1

1. Vind die grootste radius van die ellips. Dit is die afstand vanaf die middel van die ellips tot by die uiterste rand van die ellips. Beskou dit die radius van die `dik` deel van die ellips. Meet dit of soek die toepaslike etiket in die grafiek. Ons noem dit waarde a.

Jy kan dit ook die `hoof-as` noem.

Prent getiteld Bereken die oppervlakte van `n ellips Stap 2

2. Vind die kleinste radius. Soos jy dalk geraai het, is die kleinste radius die afstand vanaf die middelpunt na die naaste punt op die rand. Ons noem dit waarde b.

Hierdie radius is loodreg op die grootste radius, maar jy hoef nie hoeke vir hierdie probleem te meet nie.

Jy kan hierdie radius ook die `klein hoofas` noem.

Prent getiteld Bereken die oppervlakte van `n ellips Stap 3

3. Vermenigvuldig met pi. Die area van die ellips is a X b x. Aangesien jy twee lengte-eenhede met mekaar vermenigvuldig, is jou antwoord `n vierkant.

Byvoorbeeld, as `n ellips `n grootste radius van 5 en `n kleinste radius van 3 het, dan is die oppervlakte van die ellips 3 x 5 x π, of ongeveer 47 eenhede kwadraat.

As jy nie `n sakrekenaar het nie, of as jou sakrekenaar nie `n π-simbool het nie, gebruik `3.14` as die waarde vir pi.

Deel 2 van 2: Verstaan hoekom dit werk

Prent getiteld Bereken die oppervlakte van `n ellips Stap 4

1. Oorweeg die oppervlakte van `n sirkel. Jy onthou dalk dat die oppervlakte van `n sirkel gelyk aan πr, wat dieselfde is as π x r X r. Gestel ons wil die oppervlakte van `n sirkel bepaal asof dit `n ellips is? Ons meet die radius in een rigting: r. Meet dit met regte hoeke: ook r. Pas dit toe op die formule vir die oppervlakte van `n ellips: π x r x r! Dit blyk dat `n sirkel net `n spesifieke tipe ellips is.

Prent getiteld Bereken die oppervlakte van `n ellips Stap 5

2. Stel jou `n afgeplatte sirkel voor. Stel jou voor dat `n sirkel in die vorm van `n ellips gedruk word. Soos die sirkel verder en verder saamgepers word, sal een radius verkort en die ander langer. Die area bly dieselfde, want niks gaan uit die sirkel uit nie. Solank ons beide radiusse in die vergelyking gebruik, sal die `druk` en `rek` mekaar uitkanselleer en kry ons steeds die korrekte antwoord.