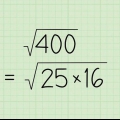As die skuif jou na `n "boks" bokant die towervierkant neem, bly in daardie blokkie se kolom, maar plaas die nommer in die onderste ry van daardie kolom. As die skuif jou na `n blokkie regs van die towervierkant neem, bly in daardie ry, maar plaas die nommer in die kolom van daardie ry, heel links van die vierkant. As die skuif jou na `n blokkie neem wat reeds `n nommer het, gaan terug na die vorige blokkie wat ingevul is, en plaas die volgende nommer direk bo dit. 

som = [6 * (62 + 1)] / 2 som = [6 * (36 + 1)] / 2 som = (6 * 37) / 2 som = 222 / 2 Die towerkonstante van `n 6x6 vierkant is 222/2, of 111. Alle rye, kolomme en diagonale moet bymekaar getel word om hierdie getal te lewer. 
Dus, vir elke 6x6 vierkant, word elke kwadrant `n 3x3 vierkant. 
In die voorbeeld van `n 6x6 vierkant word Kwadrant A opgelos met die getalle van 1-9; Kwadrant B met dié van 10-18; Kwadrant C met 19-27, en Kwadrant D met 28-36. 
Behandel die eerste nommer van elke kwadrant asof dit `n een is. Plaas dit in die middelste boks op die boonste ry van elke kwadrant. Behandel elke kwadrant as `n klein towervierkant. Selfs as die boks in `n aangrensende kwadrant beskikbaar is, ignoreer dit en spring na die `uitsonderingsreël` wat by hierdie situasie pas. 
Gebruik ’n potlood om al die blokkies in die boonste ry te merk totdat jy die middelste boks van Kwadrant A bereik. So in `n 6x6 vierkant merk jy blokkie 1 (met die nommer 8), maar in `n 10x10 vierkant merk jy blokkies 1 en 2 (met die nommers 17 en 24, onderskeidelik). Merk `n vierkant met die blokkies wat jy sopas as die boonste ry gemerk het. As jy net een blokkie gemerk het, sal jou vierkant uit nie meer as een blokkie bestaan nie. Ons noem dit Merk A-1. Dus, in `n 10x10 magiese vierkant, bestaan merker A-1 uit blokkies 1 en 2 in rye 1 en 2, wat `n 2x2 vierkant in die boonste linkerkwadrant skep. Slaan die nommer in die eerste kolom oor in die ry direk onder Merker A-1 en merk dan soveel blokkies van kant tot kant as wat jy in Merker A-1 aangedui het. Ons noem hierdie middelste ry Merking A-2. Seleksie A-3 is `n boks soortgelyk aan A-1, maar geplaas in die onderste linkerhoek van die kwadrant. Seleksie A-1, A-2 en A-3 vorm saam Merker A. Herhaal hierdie proses in Kwadrant D en skep `n identiese merkerarea, Merker D. 

Hier is twee beelde van `n 14x14 Magic Square voor en na beide skakelaars. Die skakeloppervlak van Kwadrant A is in blou gemerk, die oppervlak vir Kwadrant D is groen, vir Kwadrant C geel en vir Kwadrant B oranje. Magic Square van 14x14 voor die skakelaar (stappe 6, 7 en 8) Magic Square van 14x14 nadat die vervangings uitgevoer is (stappe 6, 7 en 8) 

som = [4 * (42 + 1)] / 2 som = [4 * (16 + 1)] / 2 som = (4 * 17) / 2 som = 68/2 Die towerkonstante van `n 4x4 vierkant is 68/2, of 34. Alle rye, kolomme en hoeklyne moet hierdie getal vorm. 
Merk net die vier hoekblokkies in `n 4x4-vierkant. In `n 8x8 vierkant is elke merker `n 2x2 area in die hoeke. In `n 12x12 vierkant is elke merker `n 3x3 area in die hoeke, ens. 
In `n 4x4-vierkant is die Sentrale Merker `n 2x2-area in die middel. In `n 8x8-vierkant is die Sentrale Merker `n 4x4-area in die middel, ens. 
1 in die boonste linker boks en 4 in die boonste regterkantste boks 6 en 7 in die middelste blokkies in Ry 2 10 en 11 in die middelste blokkies in Ry 3 13 in die onderste linker boks en 16 in die onderste regter boks. 
15 en 14 in die middelste blokkies in Ry 1 12 in die boks heel links en 9 in die boks heel regs in ry 2 8 in die boks heel links en 5 in die boks heel regs in ry 3 3 en 2 in die middelste blokkies in Ry 4 Op hierdie punt moet alle kolomme, rye en diagonale `n som gelyk aan die voorheen berekende towerkonstante hê.
Los magiese blokkies op
Inhoud
Magiese vierkante het net in gewildheid gegroei sedert die opkoms van wiskunde-gebaseerde speletjies soos Sudoku. `n Magiese vierkant is `n rangskikking van getalle in `n vierkant op so `n manier dat die som van elke ry, kolom en diagonaal `n konstante getal is, die sogenaamde towerkonstante. Hierdie artikel gaan verduidelik hoe om enige soort towervierkant op te los, of dit nou `n onewe, enkel ewe of dubbel ewe vierkant is.
Trappe
Metode 1 van 3: Los `n vreemde towervierkant op

1. Bereken die towerkonstante. Jy kan hierdie getal vind deur `n eenvoudige wiskundige formule te gebruik, waar n = die aantal rye of kolomme in jou towervierkant. So, byvoorbeeld, in `n 3x3 magiese vierkant, n = 3. Die towerkonstante = [n * (n2 + 1)] / 2. So in die voorbeeld van die 3x3 vierkant:
- som = [3 * (32 + 1)] / 2
- som = [3 * (9 + 1)] / 2
- som = (3 * 10) / 2
- som = 30/2
- Die towerkonstante van `n 3x3 vierkant is 30/2, of 15.
- Alle rye, kolomme en hoeklyne het hierdie getal as som.

2. Plaas die nommer 1 in die middelste blokkie van die boonste ry. Dit is altyd die punt waar jy begin as jou magiese vierkant van sye `n onewe aantal sye het, maak nie saak hoe groot of klein daardie getal is nie. Dus, as jy `n 3x3 vierkant het, plaas die nommer 1 in blokkie 2; in `n 15x15 vierkant, plaas die nommer 1 in blokkie 8.

3. Vul die oorblywende getalle in in `n een-op, een-na-regs patroon. Jy vul altyd die getalle volgens `n reeks in (1, 2, 3, 4, ens.) deur een ry op te gaan en dan een kolom na regs. Jy merk dadelik op dat om die nommer 2 te plaas jy bo die boonste ry eindig, buite die towervierkant. Dit is goed – hoewel jy altyd die een-na-regs-metode gebruik, is daar drie uitsonderings wat ook `n voorspelbare patroon volg:
Metode 2 van 3: Los `n eenvoudige ewe magiese vierkant op

1. Verstaan wat `n eenvoudige ewe vierkant is. Almal weet dat `n ewe getal deur 2 deelbaar is, maar met magiese vierkante is daar verskillende metodes om enkel- en dubbele ewe vierkante op te los.
- `n Eenvoudige ewe vierkant het `n aantal vierkante per sy wat deelbaar is deur 2, maar nie deur 4 nie.
- Die kleinste enkele ewe magiese vierkant is 6x6, want 2x2 magiese vierkante kan nie gemaak word nie.

2. Bereken die towerkonstante. Gebruik dieselfde metode as wat jy sou met vreemde towerkwadrate: die towerkonstante = [n * (n2 + 1)] / 2, waar n = die aantal vierkante per sy. Dus, in die voorbeeld van `n 6x6 vierkant:

3. Verdeel die towervierkant in vier ewe groot kwadrante . Benoem hulle A (links bo), C (regs bo), D (links onder) en B (regs onder). Om te bepaal hoe groot elke vierkant moet wees, verdeel die aantal bokse in elke ry of kolom in die helfte.

4. Ken `n reeks getalle aan elke kwadrant toe. Kwadrant A kry `n kwart van die getalle; Kwadrant B die tweede kwartaal; Kwadrant C die derde kwartaal en Kwadrant D die laaste kwart van die totale getalreeks van `n 6x6 towervierkant.

5. Los elke kwadrant op met behulp van die towervierkantmetode met `n onewe aantal bokse per kant. Kwadrant A is maklik om in te vul aangesien dit met die nommer 1 begin, soos magiese vierkante gewoonlik doen. Kwadrante B-D begin egter met onewe getalle - 10, 19 en 28, soos vir ons voorbeeld.

6. Maak die merkers A en D. As jy dadelik probeer het om kolomme, rye en diagonale by te voeg, het jy opgemerk dat hulle nie by die towerkonstante optel nie. Jy sal `n paar bokse van die boonste linker- en onderste linkerkwadrante moet omruil om jou towervierkant te voltooi. Ons noem hierdie areas Merker A en Merker D.

7. Ruil merkers A en D om. Dit is `n 1-tot-1-uitruil. Beweeg die blokkies tussen Kwadrant A en Kwadrant D sonder om die volgorde te verander. Sodra jy dit gedoen het, moet alle rye, kolomme en diagonale in jou towervierkant die voorheen berekende towerkonstante as hul som hê.

8. Ruil een ekstra keer vir individueel selfs Magic Squares groter as 6x6. Benewens die oorskakeling vir Kwadrante A en D hierbo genoem, moet jy ook `n oorskakeling vir Kwadrante C en B doen. Merk die kolomme van die regterkant van die vierkant na links, een minder as die aantal kolomme gemerk vir hoogtepunt A-1. Ruil die waardes in Kwadrant C met die waardes in Kwadrant B vir daardie kolomme, met dieselfde een-tot-een metode.
Metode 3 van 3: Los `n dubbele ewe magiese vierkant op

1. Verstaan wat `n dubbel ewe vierkant is. `n Eenvoudige ewe vierkant het `n aantal vierkante per sy wat deelbaar is deur 2. `n Dubbele ewe vierkant het `n aantal vierkante per sy wat deelbaar is deur 4.
- Die kleinste dubbel gelyke vierkant wat gemaak kan word, is die 4x4 vierkant.

2. Bereken die towerkonstante. Gebruik dieselfde metode as vir die onewe of enkelvoud ewe magiese vierkante: die towerkonstante = [n * (n2 + 1)] / 2, waar n = die aantal vierkante per sy. Dus, in die voorbeeld van `n 4x4 vierkant:

3. Pas merkers A-D toe. In elke hoek van die towervierkant, plaas `n klein vierkant met sye van n/4, waar n = die lengte van een sy van die hele towervierkant. Benoem hulle teenkloksgewys as Merkers A, B, C en D.

4. Plaas die sentrale merk. Merk al die blokkies in die middel van die towervierkant in `n vierkantige area van lengte n/2, waar n = die lengte van elke sy van `n volledige towervierkant. Die Sentrale Merker moet nie met Merkers A-D oorvleuel nie, maar moet hulle in die hoeke raak.

5. Vul die magiese vierkant in, maar slegs in die gemerkte areas. Begin om jou towervierkantgetalle van links na regs in te vul, maar plaas net `n nommer as die blokkie binne `n merker val. Dus, in `n 4x4-boks, vul die volgende blokkies in:

6. Vul die res van die towervierkant in deur agteruit te tel. Dit is in wese die omgekeerde van die vorige stap. Begin weer met die blokkie links bo, maar slaan hierdie keer alle blokkies oor wat in die gemerkte area val, en vul die ongeselekteerde blokkies in deur terug te tel. Begin met die grootste getal in jou getallereeks. Dus, in `n 4x4 magiese vierkant, vul in:
Wenke
- Probeer variasies op hierdie stappe om jou eie oplossingsmetodes te ontdek.
Benodigdhede
- Potlood
- Papier
- Uitveër
Artikels oor die onderwerp "Los magiese blokkies op"
Оцените, пожалуйста статью
Gewilde