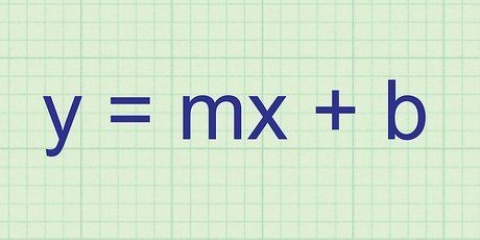Funksies word dikwels geskryf as  Dit beteken dat die funksie
Dit beteken dat die funksie  tel altyd 3 by die getal waarvoor jy het
tel altyd 3 by die getal waarvoor jy het  voltooi. As jy 2 invoer, skryf jy neer
voltooi. As jy 2 invoer, skryf jy neer  of
of 
Funksies kan ook komplekse bewegings vertoon. NASA het byvoorbeeld `n funksie om die spoed van `n vuurpyl te beskryf, gebaseer op die brandstofverbruiktempo, windweerstand en die gewig van die vuurpyl. 

Limiete is die maklikste om op `n grafiek te visualiseer - byvoorbeeld is daar punte wat naby aan `n grafiek raak, maar nooit heeltemal nie? Limiete kan getal, oneindig of selfs nie bestaan nie. Byvoorbeeld, met die optelvolgorde 1 + 2 + 2 + 2 + 2 + ... en dit gaan onbepaald aan, dan word die finale getal oneindig groot. Die limiet word dan oneindig. 
Algebra. Jy moet die verskillende prosesse verstaan en in staat wees om vergelykings en stelsels vergelykings met veelvuldige veranderlikes op te los. Verstaan die basiese beginsels van versamelings. Oefen om grafieke te maak. Meetkunde. Meetkunde is die studie van vorms. Jy moet die basiese kennis hê van driehoeke, reghoeke en sirkels, en hoe om dinge soos omtrek en oppervlakte te bereken. Verstaan hoeke, lyne en koördinate trigonometrie. Trigonometrie is die tak van wiskunde wat gemoeid is met die eienskappe van sirkels en reghoekige driehoeke. Weet hoe om trigonometriese identiteite, grafieke, funksies en inverse trigonometriese funksies te gebruik. 
Baie slimfone en tablette bied vandag goedkoop dog effektiewe grafiese toepassings as jy nie `n grafiese sakrekenaar wil of kan koop nie. 

Versnelling is `n afgeleide - dit vertel jou hoe vinnig iets versnel of vertraag, dit wil sê hoe sy spoed verander. 
Die helling van die lyn is die verandering in y gedeel deur die verandering in x`.` Hoe groter die helling die helling, hoe steiler die lyn. Steil lyne verandering verteenwoordig dus `n vinnige verandering. Verfris jou kennis oor die bepaling van die helling van `n lyn as dit `n bietjie gesink het. 
Byvoorbeeld, in  jy kan enige twee punte kies en die helling bereken. neem
jy kan enige twee punte kies en die helling bereken. neem  en
en  Die helling tussen hierdie punte is dan gelyk aan
Die helling tussen hierdie punte is dan gelyk aan  Dit beteken dat die verandering tussen
Dit beteken dat die verandering tussen  en
en  gelyk aan 2.
gelyk aan 2. 
Wetenskaplikes ondersoek byvoorbeeld hoe vinnig sommige spesies uitsterf om hulle te red. Meer diere vrek egter in die winter as in die somer, daarom is dit nie nuttig om die tempo van verandering oor die hele jaar te bestudeer nie - dit is beter om die tempo van verandering binne `n kleiner tydperk, soos van 1 Julie tot 1 Augustus te bepaal. 
Dink aan die voorbeeld waar jy aanhou om 1 deur 2 te deel, en daarmee saam 1/2, 1/4, 1/8, ens. kry. So op die ou end kom jy naby aan nul, en die antwoord is `amper nul`. Die punte is so naby aan mekaar dat hulle `amper gelyk` is. Dit is die aard van afgeleides. 

Daar is verskillende notasies vir afgeleides. In die vorige stap is afgeleides aangedui met `n karet – die afgeleide van  skryf dit dan neer as
skryf dit dan neer as  Dit word Lagrange se notasie genoem.
Dit word Lagrange se notasie genoem. Daar is `n ander manier wat dikwels gebruik word om afgeleides te skryf. In plaas van met `n sorg, let jy op  Onthou dat die funksie
Onthou dat die funksie  hang af van die veranderlike
hang af van die veranderlike  So skryf ons die afgeleide as
So skryf ons die afgeleide as  --- die afgeleide van
--- die afgeleide van  tot
tot Dit word Leibniz . se notasie genoem.
Dit word Leibniz . se notasie genoem. 
Hoe vinnig beweeg die albaster?? Teen watter spoed verander die posisie (of afgeleide) van die bewegende albaster?? Ons noem hierdie afgeleide `spoed`. Rol die albaster by `n oprit af en kyk hoe die spoed verander. Wat is die tempo van verandering, of afgeleide, van die spoed van die albaster?? Hierdie afgeleide is wat ons `versnelling` noem. Rol die albaster langs `n golwende baan, soos `n tuimeltrein. Hoeveel kry die albaster spoed wanneer dit afrol, en hoeveel vertraag die albaster opdraand?? Hoe vinnig gaan die albaster presies wanneer dit halfpad op die eerste heuwel is? Dit is dan die oombliklike tempo van verandering, of die afgeleide, van daardie albaster op daardie een spesifieke punt. 




Gestel jy tel `n klomp klein segmente onder die grafiek bymekaar, en dat die breedte van elke segment amper nul is. 
Die eerste simbool,  is die simbool vir integrasie (dit is eintlik `n uitgerekte S).
is die simbool vir integrasie (dit is eintlik `n uitgerekte S). Die tweede deel,  is die funksie. As dit binne die integraal is, word dit de genoem integrale.
is die funksie. As dit binne die integraal is, word dit de genoem integrale. En uiteindelik die  aan die einde, wat jou vertel watter veranderlike jy integreer en met watter. Omdat die funksie
aan die einde, wat jou vertel watter veranderlike jy integreer en met watter. Omdat die funksie  hang af van
hang af van  is dit waarteen jy integreer.
is dit waarteen jy integreer. Onthou dat die veranderlike wat jy integreer dalk nie altyd is nie  sal wees, wees dus versigtig wat jy neerskryf.
sal wees, wees dus versigtig wat jy neerskryf. 
Integreer deur vervanging. Berekening van onbepaalde integrale. Integreer deur te deel. 
Onthou byvoorbeeld dat die afgeleide van snelheid versnelling is, dus kan jy snelheid gebruik om versnelling te vind. Maar as jy net die versnelling van iets ken (soos voorwerpe wat as gevolg van swaartekrag val), kan jy integreer om die spoed weer te vind! 
Dit laat jou toe om die volume van enige vaste stof te bepaal, solank jy `n funksie het wat dit verteenwoordig. Byvoorbeeld, jy kan `n funksie skep wat die bodem van `n meer volg, en dit dan gebruik om die volume van die meer te bepaal, of hoeveel water dit bevat.
Verstaan analise
Inhoud
Analise (ook genoem calculus) is `n tak van wiskunde wat gefokus is op limiete, funksies, afgeleides, integrale en oneindige reekse. Hierdie vak dek baie van wiskunde, en onderlê baie van die formules en vergelykings wat in fisika en meganika gebruik word. Jy sal waarskynlik verskeie jare van wiskunde op hoërskool nodig hê om analise behoorlik te verstaan, maar hierdie artikel sal jou aan die gang kry om die sleutelkonsepte te herken, sowel as `n beter begrip van die teorie.
Trappe
Deel 1 van 3: Die basiese beginsels van analise

1. Analise is die studie van hoe dinge verander. Analise is `n tak van wiskunde wat getalle en grafieke ondersoek, gewoonlik geneem uit werklike wêrelddata, en verduidelik hoe hulle verander. Alhoewel dit aanvanklik nie baie nuttig lyk nie, is analise een van die mees gebruikte vertakkings van wiskunde. Stel jou voor dat jy die gereedskap het wat jou kan vertel hoe vinnig jou besigheid op enige gegewe tydstip groei, of om die verloop van `n ruimteskip te karteer, en hoe vinnig die brandstof opgebruik word. Analise is `n belangrike hulpmiddel in ingenieurswese, ekonomie, statistiek, chemie en fisika, en het bygedra tot baie uitvindings en ontdekkings.

2. Funksies is verwantskappe tussen twee getalle en word gebruik om verwantskappe te karteer. Dit is reëls vir die verwantskap tussen getalle, en wiskundiges gebruik dit om grafieke te maak. In `n funksie het elke inset presies een uitkoms. Byvoorbeeld: in  gee enige waarde van
gee enige waarde van  `n nuwe waarde vir
`n nuwe waarde vir  In die geval dat
In die geval dat  dan is
dan is  In die geval dat
In die geval dat  , dan
, dan  Analise bestudeer altyd funksies en hoe hulle verander, deur hierdie funksies te gebruik om verwantskappe te karteer.
Analise bestudeer altyd funksies en hoe hulle verander, deur hierdie funksies te gebruik om verwantskappe te karteer.
 gee enige waarde van
gee enige waarde van  `n nuwe waarde vir
`n nuwe waarde vir  In die geval dat
In die geval dat  dan is
dan is  In die geval dat
In die geval dat  , dan
, dan  Analise bestudeer altyd funksies en hoe hulle verander, deur hierdie funksies te gebruik om verwantskappe te karteer.
Analise bestudeer altyd funksies en hoe hulle verander, deur hierdie funksies te gebruik om verwantskappe te karteer. Dit beteken dat die funksie
Dit beteken dat die funksie  tel altyd 3 by die getal waarvoor jy het
tel altyd 3 by die getal waarvoor jy het  voltooi. As jy 2 invoer, skryf jy neer
voltooi. As jy 2 invoer, skryf jy neer  of
of 

3. Dink aan die konsep van oneindigheid. Oneindigheid is die voortdurende herhaling van `n proses. Dit is nie `n spesifieke plek nie (jy kan nie tot in oneindigheid gaan nie), maar eerder die gedrag van `n getal of vergelyking, as dit vir ewig gedoen word. Dit is belangrik om verandering te bestudeer: jy wil dalk weet hoe vinnig jou motor op `n gegewe oomblik beweeg, maar is dit hoe vinnig jou motor gedurende die huidige sekonde beweeg?? millisekonde? Nanosekonde? Jy kan oneindig kleiner stukkies tyd vind om selfs meer presies te wees, en dit is wanneer ontleding inskop.

4. Verstaan die konsep van limiete. ’n Limiet vertel jou wat gebeur wanneer iets oneindig nader. Neem die getal 1 en deel dit deur 2. Hou aan om deur 2 te deel, oor en oor. 1 word ½ en dan 1/4, 1/8, 1/16, 1/32, ens. Elke keer word die getal kleiner en kleiner, `nader aan` nul. Maar waar hou dit op? Hoeveel keer moet jy 1 deur 2 deel om nul te kry?? In plaas daarvan om hierdie vraag te beantwoord, stel jy in ontleding `n voor beperk In hierdie geval is die limiet.

5. Gaan deur die noodsaaklike wiskundige konsepte van algebra, trigonometrie en die basiese beginsels van wiskunde. Ontleding maak staat op baie van die wiskunde wat jy voorheen geleer het. Om goed vertroud te wees met alle onderwerpe maak dit baie makliker om analise te leer en te verstaan. Sommige onderwerpe om jou kennis van te verfris is:

6. Kry `n grafiese sakrekenaar. Ontleding is nie maklik om te verstaan sonder om te sien wat jy doen nie. Grafiese sakrekenaars maak funksies visueel sodat jy beter kan verstaan met watter vergelykings jy te doen het. Dikwels word die limiete ook op die skerm vertoon, en die afgeleides en funksies word outomaties bereken.
Deel 2 van 3: Verstaan afgeleides

1. Analise word gebruik om `verandering op `n spesifieke oomblik` te bestudeer. Om te weet hoekom iets op `n presiese oomblik verander, is die kern van analise. Byvoorbeeld, analise gee jou nie net die spoed van `n motor nie, maar ook hoeveel daardie spoed op `n gegewe oomblik verander. Dit is een van die eenvoudigste gebruike van analise, maar baie belangrik. Stel jou voor hoe belangrik sulke inligting is om die spoed te bepaal wat nodig is om `n ruimteskip na die maan te kry!
- Bepaling van verandering op `n gegewe oomblik het onderskei. Differensiasie is die eerste van die twee groot vertakkings van analise.

2. Gebruik afgeleides om te verstaan hoe dinge op `n gegewe oomblik verander. `n `Afgeleide` is `n spoggerige woord vir iets wat studente dikwels senuweeagtig maak. Die konsep self is egter nie so moeilik om te verstaan nie - dit beteken net `hoe vinnig iets verander`. Die afgeleides wat jy die meeste in die daaglikse lewe sal teëkom het te make met spoed. Jy noem dit egter gewoonlik nie `die afgeleide van spoed` nie, maar bloot `versnelling`.

3. Weet dat die tempo van verandering gelyk is aan die helling tussen twee punte. Dit is een van die belangrikste ontdekkings van analise. Die tempo van verandering tussen twee punte is gelyk aan die helling van die lyn tussen daardie twee punte. Dink net aan `n eenvoudige lyn, soos dié van die vergelyking  Die helling van die lyn is 3, wat beteken dat vir elke nuwe waarde van
Die helling van die lyn is 3, wat beteken dat vir elke nuwe waarde van 
 verander met 3. Die helling is dieselfde as die tempo van verandering: `n helling van drie beteken dat die lyn met 3 verander (drie keer groter word) vir elke verandering in
verander met 3. Die helling is dieselfde as die tempo van verandering: `n helling van drie beteken dat die lyn met 3 verander (drie keer groter word) vir elke verandering in  Wanneer
Wanneer  wanneer
wanneer 
 Die helling van die lyn is 3, wat beteken dat vir elke nuwe waarde van
Die helling van die lyn is 3, wat beteken dat vir elke nuwe waarde van 
 verander met 3. Die helling is dieselfde as die tempo van verandering: `n helling van drie beteken dat die lyn met 3 verander (drie keer groter word) vir elke verandering in
verander met 3. Die helling is dieselfde as die tempo van verandering: `n helling van drie beteken dat die lyn met 3 verander (drie keer groter word) vir elke verandering in  Wanneer
Wanneer  wanneer
wanneer 

4. Weet dat jy die helling van geboë lyne kan bepaal. Die bepaling van die helling van `n reguit lyn is relatief eenvoudig: hoeveel verander  vir enige waarde van
vir enige waarde van  Maar komplekse vergelykings soos
Maar komplekse vergelykings soos  vir `n kromme, is baie moeiliker om te bepaal. Jy kan egter steeds die tempo van verandering tussen twee punte bepaal -- trek net `n lyn tussen die twee punte en bereken die helling.
vir `n kromme, is baie moeiliker om te bepaal. Jy kan egter steeds die tempo van verandering tussen twee punte bepaal -- trek net `n lyn tussen die twee punte en bereken die helling.
 vir enige waarde van
vir enige waarde van  Maar komplekse vergelykings soos
Maar komplekse vergelykings soos  vir `n kromme, is baie moeiliker om te bepaal. Jy kan egter steeds die tempo van verandering tussen twee punte bepaal -- trek net `n lyn tussen die twee punte en bereken die helling.
vir `n kromme, is baie moeiliker om te bepaal. Jy kan egter steeds die tempo van verandering tussen twee punte bepaal -- trek net `n lyn tussen die twee punte en bereken die helling. jy kan enige twee punte kies en die helling bereken. neem
jy kan enige twee punte kies en die helling bereken. neem  en
en  Die helling tussen hierdie punte is dan gelyk aan
Die helling tussen hierdie punte is dan gelyk aan  Dit beteken dat die verandering tussen
Dit beteken dat die verandering tussen  en
en  gelyk aan 2.
gelyk aan 2.
5. As jy die verandering meer akkuraat wil bereken, maak seker dat die punte nader aan mekaar is. Hoe nader jy die twee punte kies, hoe meer akkuraat is jou antwoord. Gestel jy wil weet hoeveel jou motor versnel wanneer jy die versnellerpedaal druk. Jy wil nie die verandering in spoed tussen jou huis en die supermark meet nie, maar die verandering in spoed vanaf die oomblik dat jy op die versneller trap. Hoe nader jou lesing aan daardie breukdeel van `n sekonde kom, hoe meer akkuraat is jou berekening van die verandering.

6. Gebruik oneindig kort lyne om die `oombliklike tempo van verandering` te bepaal, of vind die afgeleide. Dit is waar ontleding dikwels `n bietjie verwarrend raak, maar dit is eintlik die resultaat van twee eenvoudige feite. Eerstens weet jy dat die helling van `n lyn gelyk is aan hoe vinnig daardie lyn verander. Tweedens, jy weet dat hoe nader die punte van die lyn aan mekaar is, hoe meer akkuraat sal die lesing word. Maar hoe vind jy die tempo van verandering by `n gegewe punt as die helling die verhouding tussen twee punte is? Die antwoord: Jy kies twee punte wat oneindig naby aan mekaar is.

7. Leer hoe om verskillende afgeleides te bepaal. Daar is baie verskillende tegnieke om `n afgeleide te vind, afhangende van die vergelyking, maar die meeste van hulle maak sin sodra jy die basiese beginsels van afgeleides hierbo onthou. Alle afgeleides is `n manier om die helling van `n `oneindig klein` lyn te vind. Noudat jy meer van afgeleide teorie weet, is baie van die werk om die antwoorde te vind.

8. Bepaal die afgeleide vergelykings om die tempo van verandering te eniger tyd te voorspel. Dit is nuttig om die tempo van verandering op enige gegewe oomblik met behulp van afgeleides te bepaal, maar die skoonheid van analise is dat jy `n nuwe model vir enige funksie kan skep. Die afgeleide van  byvoorbeeld is
byvoorbeeld is  Dit beteken dat jy die afgeleide vir enige punt op `n grafiek kan vind
Dit beteken dat jy die afgeleide vir enige punt op `n grafiek kan vind  deur die afgeleide te vervang. Op die punt
deur die afgeleide te vervang. Op die punt  waardeur
waardeur  is die afgeleide 4, want
is die afgeleide 4, want 
 byvoorbeeld is
byvoorbeeld is  Dit beteken dat jy die afgeleide vir enige punt op `n grafiek kan vind
Dit beteken dat jy die afgeleide vir enige punt op `n grafiek kan vind  deur die afgeleide te vervang. Op die punt
deur die afgeleide te vervang. Op die punt  waardeur
waardeur  is die afgeleide 4, want
is die afgeleide 4, want 
 skryf dit dan neer as
skryf dit dan neer as  Dit word Lagrange se notasie genoem.
Dit word Lagrange se notasie genoem. Onthou dat die funksie
Onthou dat die funksie  hang af van die veranderlike
hang af van die veranderlike  So skryf ons die afgeleide as
So skryf ons die afgeleide as  --- die afgeleide van
--- die afgeleide van  tot
tot Dit word Leibniz . se notasie genoem.
Dit word Leibniz . se notasie genoem.
9. Probeer om praktiese voorbeelde van afgeleides te onthou, as jy dit moeilik vind om te verstaan. Die eenvoudigste voorbeeld is gebaseer op spoed, wat baie verskillende afgeleides insluit wat ons elke dag teëkom. Moenie vergeet nie: `n afgeleide is `n maatstaf van hoe vinnig iets verander. Dink aan `n eenvoudige eksperiment. Jy rol `n albaster op `n tafel en meet hoe ver dit elke keer beweeg en hoe vinnig. Stel jou nou voor dat die rollende albaster `n lyn op `n grafiek volg - jy gebruik afgeleides om die oombliklike veranderinge enige tyd op daardie lyn te meet.
Deel 3 van 3: Verstaan integrale

1. Weet dat jy analise kan gebruik om komplekse areas en volumes te vind. Met ontleding kan jy komplekse vorms meet wat andersins moeilik is om te meet. Dink byvoorbeeld aan die vraag om te wil weet hoeveel water daar in `n lang, onreëlmatige gevormde meer is - dit is onmoontlik om elke liter water individueel te meet of om `n liniaal te gebruik om die vorm van die meer te meet. Met ontleding kan jy bestudeer hoe die rande van die meer verander, en dan daardie inligting gebruik om uit te vind hoeveel water dit bevat.
- Die maak van meetkundige modelle en die studie van volumes het integreer. Integraalrekening is die tweede belangrike tak van analise.

2. Weet dat integrasie die area onder `n grafiek is. Integrasie word gebruik om die spasie onder `n lyn te meet, wat jou toelaat om die area van vreemde of onreëlmatige vorms te bepaal. Neem die vergelyking  Dit lyk soos `n omgekeerde `U`. Jy kan bereken hoeveel spasie daar onder die U is deur integraalrekening te gebruik. Jy wonder dalk wat die punt daarvan is, maar dink aan die gebruik daarvan in die vervaardigingsprosesse -- jy kan `n funksie skep wat soos `n nuwe deel lyk, en integrale rekenkunde gebruik om die oppervlakte van daardie deel te vind, en om help jou om die regte hoeveelheid materiaal te bestel.
Dit lyk soos `n omgekeerde `U`. Jy kan bereken hoeveel spasie daar onder die U is deur integraalrekening te gebruik. Jy wonder dalk wat die punt daarvan is, maar dink aan die gebruik daarvan in die vervaardigingsprosesse -- jy kan `n funksie skep wat soos `n nuwe deel lyk, en integrale rekenkunde gebruik om die oppervlakte van daardie deel te vind, en om help jou om die regte hoeveelheid materiaal te bestel.
 Dit lyk soos `n omgekeerde `U`. Jy kan bereken hoeveel spasie daar onder die U is deur integraalrekening te gebruik. Jy wonder dalk wat die punt daarvan is, maar dink aan die gebruik daarvan in die vervaardigingsprosesse -- jy kan `n funksie skep wat soos `n nuwe deel lyk, en integrale rekenkunde gebruik om die oppervlakte van daardie deel te vind, en om help jou om die regte hoeveelheid materiaal te bestel.
Dit lyk soos `n omgekeerde `U`. Jy kan bereken hoeveel spasie daar onder die U is deur integraalrekening te gebruik. Jy wonder dalk wat die punt daarvan is, maar dink aan die gebruik daarvan in die vervaardigingsprosesse -- jy kan `n funksie skep wat soos `n nuwe deel lyk, en integrale rekenkunde gebruik om die oppervlakte van daardie deel te vind, en om help jou om die regte hoeveelheid materiaal te bestel.
3. Weet om `n area te kies om te integreer. Jy kan nie net `n hele funksie integreer nie. Byvoorbeeld,  is `n diagonale lyn wat vir ewig aanhou, en jy kan nie die hele ding integreer nie, want dit sal nooit ophou nie. Wanneer u funksies integreer, moet u `n area kies, soos alle punte tussenin
is `n diagonale lyn wat vir ewig aanhou, en jy kan nie die hele ding integreer nie, want dit sal nooit ophou nie. Wanneer u funksies integreer, moet u `n area kies, soos alle punte tussenin en
en 
 is `n diagonale lyn wat vir ewig aanhou, en jy kan nie die hele ding integreer nie, want dit sal nooit ophou nie. Wanneer u funksies integreer, moet u `n area kies, soos alle punte tussenin
is `n diagonale lyn wat vir ewig aanhou, en jy kan nie die hele ding integreer nie, want dit sal nooit ophou nie. Wanneer u funksies integreer, moet u `n area kies, soos alle punte tussenin en
en 

4. Hoe bereken jy die oppervlakte van `n reghoek?. Gestel jy het `n plat lyn bokant `n grafiek, soos  Om die area daaronder te vind, vind die area van `n reghoek tussen
Om die area daaronder te vind, vind die area van `n reghoek tussen  en
en  Dit is maklik om te meet, maar dit sal nie met golwende lyne werk nie, want jy kan dit nie maklik na reghoeke omskakel nie.
Dit is maklik om te meet, maar dit sal nie met golwende lyne werk nie, want jy kan dit nie maklik na reghoeke omskakel nie.
 Om die area daaronder te vind, vind die area van `n reghoek tussen
Om die area daaronder te vind, vind die area van `n reghoek tussen  en
en  Dit is maklik om te meet, maar dit sal nie met golwende lyne werk nie, want jy kan dit nie maklik na reghoeke omskakel nie.
Dit is maklik om te meet, maar dit sal nie met golwende lyne werk nie, want jy kan dit nie maklik na reghoeke omskakel nie.
5. Weet dat in integraalrekening baie klein reghoeke bymekaar getel word om die oppervlakte van `n area te vind. As jy `n kromme geweldig vergroot, lyk dit soos `n reguit lyn. Jy sien dit elke dag -- jy kan nie die kromming van die Aarde sien nie, want jy is so naby aan die Aarde se oppervlak. Integrasie skep `n oneindige aantal klein reghoeke onder `n kromme wat so klein is dat hulle basies plat is, wat jou toelaat om hulle te tel. Al hierdie reghoeke saamgevoeg vorm die area van die area onder `n kromme.

6. Weet hoe om integrale korrek te lees en te skryf. Integrale bestaan uit 4 dele. `n Tipiese integraal lyk soos volg:


 is die simbool vir integrasie (dit is eintlik `n uitgerekte S).
is die simbool vir integrasie (dit is eintlik `n uitgerekte S). is die funksie. As dit binne die integraal is, word dit de genoem integrale.
is die funksie. As dit binne die integraal is, word dit de genoem integrale. aan die einde, wat jou vertel watter veranderlike jy integreer en met watter. Omdat die funksie
aan die einde, wat jou vertel watter veranderlike jy integreer en met watter. Omdat die funksie  hang af van
hang af van  is dit waarteen jy integreer.
is dit waarteen jy integreer. sal wees, wees dus versigtig wat jy neerskryf.
sal wees, wees dus versigtig wat jy neerskryf.
7. Kom meer te wete oor die vind van integrale. Integraalrekening kom in baie vorme voor, en jy moet baie verskillende formules leer om elke funksie te integreer. Hulle volg egter almal die beginsels wat hierbo uiteengesit is: integrasie is die som van `n oneindige aantal dinge.

8. Weet dat integrasie die omgekeerde van differensiasie is, en omgekeerd. Dit is `n reël van analise wat so belangrik is dat dit sy eie naam gekry het: die Fundamentele Stelling van Integrale Rekening. Aangesien integrasie en differensiasie so nou verwant is, kan `n kombinasie van die twee gebruik word om die tempo van verandering, versnelling, snelheid, ligging, beweging, ens. om te bepaal, maak nie saak watter inligting jy het nie.

9. Weet dat integrasie jou ook toelaat om die volume van 3D-voorwerpe te beheer. Om `n plat vorm te draai is `n manier om 3D-vaste stowwe te skep. Stel jou net `n muntstuk op die tafel voor wat draai - let op hoe die munt lyk asof dit die vorm van `n bol aanneem soos dit draai. Hierdie konsep laat jou toe om volume te bepaal deur `n proses bekend as `volume deur rotasie`.
Wenke
- Oefening maak perfek, so doen die oefenoefeninge in jou handboek – selfs dié wat jou onderwyser nie gespesifiseer het nie – en kontroleer jou antwoorde sodat jy die konsepte beter verstaan.
- As jy iets nie kan uitvind nie, vra jou onderwyser.
Artikels oor die onderwerp "Verstaan analise"
Оцените, пожалуйста статью
Gewilde