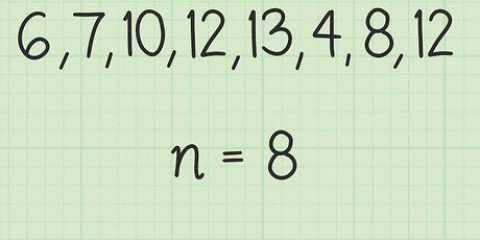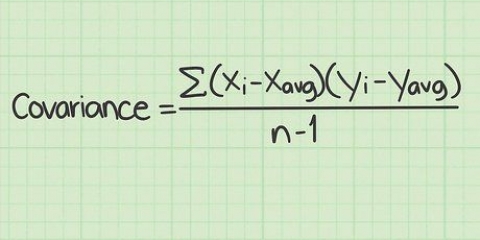As `n algemene reël word die betekenisvlak (of alfa) dikwels op 0.05 gestel, wat beteken dat die waarskynlikheid om per ongeluk die verskille in jou data waar te neem slegs 5% is. `n Hoër vertrouensvlak (en dus `n laer p-waarde) beteken dat die resultate meer betekenisvol is. As jy wil hê die data moet meer betroubaar wees, stel die p-waarde onder 0.01. Laer p-waardes word algemeen in die industrie gebruik wanneer produkte ontfout word. Dit is baie belangrik om groot vertroue te kan hê dat elke onderdeel presies werk soos dit moet. Vir die meeste eksperimente na `n hipotese is `n betekenisvlak van 0,05 aanvaarbaar. 
As jy nie seker is of jou data bo of onder die kontrolegroep is nie, gebruik `n tweeledige toets. Laat jou toe om te toets vir betekenis in beide rigtings. As jy weet watter rigting jou data geneig is om te beweeg, gebruik `n eensydige toets. In die voorbeeld wat gegee word, verwag jy dat die studente se grade sal verbeter; daarom gebruik jy `n eensydige toets. 
Navorsers doen gewoonlik `n klein loodsstudie om hul sterkte-analise in te lig en om die steekproefgrootte te bepaal wat nodig is vir `n groter, meer omvattende studie. As jy nie die hulpbronne het om `n komplekse loodsstudie te doen nie, maak `n paar skattings van moontlike gemiddeldes gebaseer op die lees van die literatuur en die studies wat ander individue moontlik gedoen het. Dit sal jou `n goeie beginpunt gee vir steekproefgrootte om mee te begin. 

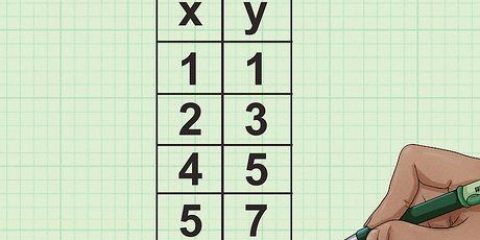
Om byvoorbeeld die gemiddelde graad van die groep te vind wat die materiaal voor die klas gelees het, kom ons kyk na sommige data. Vir eenvoud gebruik ons `n datastel van 5 punte: 90, 91, 85, 83 en 94. Voeg al die data bymekaar: 90 + 91 + 85 + 83 + 94 = 443. Deel die som deur die aantal data, N = 5:443 / 5 = 88,6. Die gemiddelde graad van hierdie groep is 88,6. 
(90 – 88.6), (91–88.6), (85–88.6), (83–88.6) en (94–88.6). Die berekende getalle is nou 1.4, 2.4, -3.6, -5.6 en 5.4. 
In ons voorbeeld werk ons nou met 1.96 5.76, 12.96, 31.36 en 29.16. Deur hierdie vierkante bymekaar te tel, gee jy: 1.96 + 5.76 + 12.96 + 31.36 + 29.16 = 81.2. 
Trek af: N – 1 = 5 – 1 = 4 Deel: 81.2/4 = 20.3 
In ons voorbeeld is die standaardafwyking van die finale grade van studente wat die materiaal voor die klas gelees het: s = √20.3 = 4.51. 

µ1 is die gemiddelde van die eerste groep. µ2 is die gemiddelde van die tweede groep. sd is die variansie tussen die monsters. Gebruik die groter gemiddelde as µ1, dus het jy nie `n negatiewe waarde vir t nie. In ons voorbeeld, kom ons sê die steekproefgemiddelde vir Groep 2 (diegene wat nie gelees het nie) was 80. Die t-telling is dan: t = (µ1 – µ2)/sd = (88.6 – 80)/3.29 = 2.61. 

met 8 d.f. en `n t-telling van 2,61, val die p-waarde vir `n eensydige toets tussen 0,01 en 0,025. Omdat ons vasgestelde betekenisvlak minder as of gelyk aan 0.05 is, is ons data statisties beduidend. Met hierdie data verwerp ons die nulhipotese en aanvaar die alternatiewe hipotese: Studente wat die materiaal voor klas lees, kry beter finale punte. 
Evalueer statistiese betekenisvolheid
Inhoud
Hipotesetoetsing word deur statistiese analise ondersteun. Statistiese betekenisvolheid word bereken vanaf `n p-waarde, wat die waarskynlikheid van die waargenome resultaat aandui, gegewe dat `n bepaalde stelling (die nulhipotese) bevredig is. As hierdie p-waarde minder is as die gestelde betekenisvlak (gewoonlik 0.05), dan kan die eksperimenteerder aanvaar dat die nulhipotese vals is en die alternatiewe hipotese aanvaar. Deur `n eenvoudige t-toets te gebruik, kan jy `n p-waarde bereken en die betekenisvolheid tussen twee verskillende groepe van `n datastel vergelyk.
Trappe
Deel 1 van 3: Stel jou eksperiment op

1. Definieer jou hipotese. Die eerste stap in die assessering van statistiese betekenisvolheid is om die vraag wat beantwoord moet word te definieer en jou hipotese te stel. Die hipotese is `n stelling oor jou eksperimentele data en die verskille wat in die populasie kan bestaan. In elke eksperiment is daar beide `n nul- en `n alternatiewe hipotese. Oor die algemeen sal jy twee groepe vergelyk om te sien of hulle dieselfde of verskillend is.
- Die nulhipotese (H0) sê oor die algemeen dat daar geen verskil tussen jou twee stelle data is nie. Byvoorbeeld: studente wat die materiaal voor die klas gelees het, behaal nie beter finale punte nie.
- Die alternatiewe hipotese (Ha) is die teenoorgestelde van die nulhipotese en is die bewering wat jy probeer ondersteun met jou eksperimentele data. Byvoorbeeld: studente wat die materiaal voor die klas gelees het, behaal beter finale punte.

2. Stel die betekenisvlak om te bepaal hoe ongewoon jou data moet wees voordat dit as betekenisvol beskou kan word. Die betekenisvlak (ook alfa genoem) is die drempel wat jy stel om betekenis te bepaal. As die p-waarde minder as of gelyk is aan die vasgestelde betekenisvolheid, kan die data as statisties beduidend beskou word.

3. Besluit om `n eenkant- of tweesterttoets te gebruik. Een van die aannames wat `n t-toets maak, is dat data normaal versprei is. `n Normale verspreiding van data vorm `n klokkurwe met die meeste van die toetsdata wat in die middel val. Die t-toets is `n wiskundige toets om te sien of data buite die normaalverspreiding (bo of onder), in die `sterte` van die kromme val.

4. Bepaal die steekproefgrootte met `n kragontleding. Die krag van `n toets is die waarskynlikheid dat die verwagte resultaat waargeneem sal word, gegewe `n spesifieke steekproefgrootte. Die algemene drempel vir krag (of β) is 80%. `n Kragontleding kan `n bietjie moeilik raak sonder `n paar voorlopige data, want jy benodig inligting oor die verwagte middelwaardes tussen elke groep en hul standaardafwykings. Gebruik `n aanlyn kraganalise sakrekenaar om die optimale steekproefgrootte vir jou data te bepaal.
Deel 2 van 3: Berekening van die standaardafwyking

1. Vind die formule vir die standaardafwyking. Die standaardafwyking is `n maatstaf van die verspreiding van jou data. Dit gee jou inligting oor hoe soortgelyk elke datapunt binne jou steekproef is. Met die eerste oogopslag kan die vergelyking `n bietjie ingewikkeld lyk, maar die volgende stappe sal jou deur die berekening lei. Die formule is: s = √∑((xi – µ)/(N – 1)).
- s is die standaardafwyking.
- ∑ dui aan dat jy al die versamelde steekproefwaardes moet bymekaartel.
- Xi verteenwoordig elke individuele waarde van jou data.
- µ is die gemiddelde (of middelpunt) van jou data vir elke groep.
- N is die totaal van die steekproef.

2. Maak `n gemiddelde van die toetsdata in elke groep. Om die standaardafwyking te bereken, moet jy eers die gemiddelde toetsdata in die individuele groepe bereken. Die gemiddelde word aangedui deur die Griekse letter mu of µ. Om dit te doen, tel elke stuk data by en deel dit dan deur die totale aantal data.

3. Trek elke maatstaf van die gemiddelde af. Die volgende deel van die berekening sluit die deel (xi – µ) van die vergelyking. Jy trek elke data van die pas berekende gemiddelde af. In ons voorbeeld eindig jy met vyf aftrekkings.

4. Kwadra elkeen van hierdie getalle en tel hulle bymekaar. Elkeen van die nuwe getalle wat jy so pas bereken het, sal nou gekwadraat wees. Hierdie stap skep ook negatiewe tekens. As jy `n minus teken na hierdie stap of aan die einde van jou berekening het, het jy dalk hierdie stap vergeet.

5. Deel dit deur die grootte van die totale steekproef, minus 1. Die formule deel deur N-1, want dit maak reg vir die feit dat jy nog nie `n hele bevolking getel het nie; jy neem `n steekproef uit die populasie van alle studente om `n skatting te maak.

6. Neem die vierkantswortel. Sodra jy gedeel het deur die aantal data minus een, bereken die vierkantswortel van hierdie laaste getal. Dit is die laaste stap in die berekening van die standaardafwyking. Daar is statistiese programme wat hierdie berekening vir jou kan doen, nadat jy die rou data ingevoer het.
Deel 3 van 3: Bepaal die beduidendheid

1. Bereken die verskil tussen jou twee groepe van die steekproef. Tot op hierdie stadium het die voorbeeld slegs een van die steekproefgroepe gedek. As jy twee groepe wil vergelyk, sal jy natuurlik data van albei groepe hê. Bereken die standaardafwyking van die tweede groep toetsdata en gebruik dit om die verskil tussen die twee eksperimentele groepe te bereken. Die formule vir variansie is sd = √((s1/N1) + (s2/N2)).
- sd is die verskil tussen jou groepe.
- s1 is die standaardafwyking van groep 1, en N1 is die steekproefgrootte van groep 1.
- s2 is die standaardafwyking van groep 2, en N2 is die steekproefgrootte van groep 2.
- Ter wille van ons voorbeeld, kom ons sê dat die data van Groep 2 (studente wat nie voor die klas gelees het nie) `n steekproefgrootte van 5 en `n standaardafwyking van 5,81 gehad het. Die variansie is:
- sd = √((s1)/N1) + ((s2)/N2))
- sd = √(((4.51)/5) + ((5.81)/5)) = √((20.34/5) + (33.76/5)) = √(4.07 + 6.75) = √10.82 = 3.29.

2. Bereken die t-telling van jou data. Met `n t-telling kan jy data omskep in `n vorm wat jy dit met ander data kan vergelyk. Met t-tellings kan jy `n t-toets uitvoer om die waarskynlikheid te bereken dat twee groepe aansienlik van mekaar verskil. Die formule vir `n t-telling is: t = (µ1 – µ2)/sd.

3. Bepaal die mate van vryheid van jou monster. Wanneer die t-telling gebruik word, word die vryheidsgrade bepaal deur die steekproefgrootte te gebruik. Tel die aantal toetsdata van elke groep bymekaar en deel dan deur twee. In ons voorbeeld, die grade van vryheid; d.f.) 8, want daar was vyf data in die eerste groep en vyf in die tweede groep ((5 + 5) – 2 = 8).

4. Gebruik `n t-tabel om betekenisvolheid te bepaal. `n Tabel met t-tellings en die aantal grade van vryheid kan in `n standaardstatistiekboek of aanlyn gevind word. Kyk na die ry vryheidsgrade vir jou data en vind die p-waarde wat ooreenstem met jou t-telling.

5. Oorweeg `n opvolgstudie. Baie navorsers doen `n klein loodsstudie met `n paar metings om te verstaan hoe om `n groter studie op te stel. Nog `n studie, met meer metings, sal help om jou vertroue in jou gevolgtrekking te verhoog.
Wenke
- Statistiek is `n uitgebreide en ingewikkelde veld. Neem `n hoërskool- of hoëronderwysklas oor statistiese afleiding om statistiese betekenisvolheid beter te verstaan.
Waarskuwings
- Hierdie analise is spesifiek vir `n t-toets om die verskille tussen twee normaalverspreide populasies te toets. Jy sal dalk `n ander statistiese toets nodig hê, afhangende van die kompleksiteit van jou data-insameling.
Artikels oor die onderwerp "Evalueer statistiese betekenisvolheid"
Оцените, пожалуйста статью
Gewilde