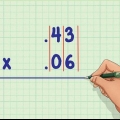
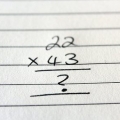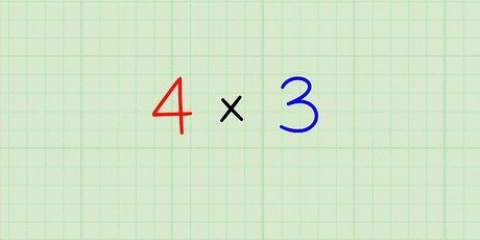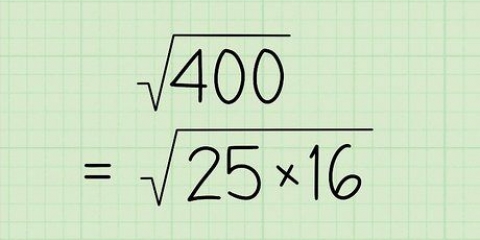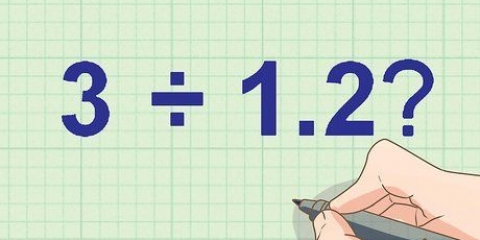Byvoorbeeld, as jy 6 x 7 wil vermenigvuldig, skryf 6 en skryf die 7 direk onder dit neer. Trek die lyn net onder 7. Alhoewel Vediese Wiskunde `n vorm van hoofrekene is wat sonder `n pen en papier gebruik kan word, kan dit nuttig wees vir diegene wat daarmee begin om `n probleem neer te skryf en sodoende die stappe beter te visualiseer. As jy egter meer vaardig is om wiskundeprobleme in jou kop op te los, kan jy net hierdie opmaak visualiseer in plaas daarvan om dit neer te skryf. 
Byvoorbeeld, om 6 x 7 te vermenigvuldig, sal jy eers 10 – 6 = 4 doen. Skryf die 4 regs van die 6. Bereken dan 10 - 7 = 3. Skryf die 3 regs van die 7, net onder die 4. Om van 10 af te trek neem die `basis` van die getalle. Die term `basis` verwys na die basis 10-getalstelsel wat in Vediese wiskunde gebruik word, sowel as die feit dat die `basisgetal` of basis as basis vir die berekeninge geneem word. Die basisse in Vediese wiskunde is 10, 100, 1000 en 100.000. Vir enkelsyfergetalle, gebruik die basis van 10, want dit is die naaste basis aan enkelsyfergetalle. 
Byvoorbeeld: vir die oorspronklike probleem 6 x 7 het jy nou byvoorbeeld 4 en 3 in die regterkolom. Bereken 4 x 3 = 12. Skryf die 2, die heel regterkantste nommer, onder die lyn. Neem die 1, die linker syfer, na die volgende stap. Om jou te help om die nommer heel links te onthou, kan jy die nommers langs mekaar skryf. Skryf egter die linker syfer `n bietjie weg van die som af, sodat jy nie deurmekaar raak nie. 
Byvoorbeeld, as die oorspronklike probleem 6 x 7 is, word die 6 bo die 7 in die linkerkolom geskryf en 4 bo 3 in die regterkolom. So jy kan óf 6 - 3 óf 7 - 4 uitvoer, wat albei gelyk is aan 3. 
Vir die oorspronklike probleem word die 6 van 6 x 7 dan aangeteken bo die 7 in die linkerkolom, en 4 bo die 3 in die regterkolom. Dan bereken jy 4 x 3 = 12, en skryf die 2 neer, die syfer heel regs, onder die lyn van die regterkolom, en onthou 1, die syfer heel links. Dan voeg jy die onthou 1 by die 3 wat uit 6 - 3 of 7 - 4 in die vorige stap voortgespruit het, met 4 as die resultaat. Skryf die 4 in die linkerkolom onder die reël van die probleem neer. 
In die voorbeeld van die probleem 6 x 7 het jy nou `n 4 in die linkerkolom en `n 2 in die regterkolom onder die reël van die probleem. Die antwoord op jou oorspronklike probleem, 6 x 7, is dus 42. 

Byvoorbeeld, wanneer 20 x 21 vermenigvuldig word, vermenigvuldig eers die 2 (die eerste, linker syfer in 20) met 2 (die eerste, linker syfer in 21), wat gelyk is aan 4. Skryf die 4 onder die vermenigvuldigingslyn in die linkerkolom. 
Byvoorbeeld, wanneer 20 x 21 vermenigvuldig word, vermenigvuldig eers die 2 (die nommer van die boonste linkerkolom in die 20) met 1 (die nommer van die onderste regterkolom in die 21), wat gelyk is aan 2. Dan vermenigvuldig jy 2 (die nommer van die onderste linkerkolom in die 21) met 0 (die nommer van die boonste regterkantste kolom in die 20), wat gelyk is aan 0. Voeg die oplossings (2 en 0) bymekaar, en jy kry 2 as `n antwoord. Skryf die 2 onder die vermenigvuldigingslyn regs van die 4 wat jy reeds onder die vermenigvuldigingslyn geskryf het. 
Byvoorbeeld, wanneer jy 20 x 21 vermenigvuldig, sal jy 0 (die boonste getal in die regterkolom) vermenigvuldig met 1 (die onderste getal in die regterkolom), wat gelyk is aan 0. Skryf 0 onder die vermenigvuldigingslyn regs van die 4 en die 2 wat jy reeds neergeskryf het. Dan sien jy dat die antwoord op jou oorspronklike vergelyking, 20 x 21, gelyk is aan 420. 

Byvoorbeeld, wanneer 121 x 151 vermenigvuldig word, vermenigvuldig eers die 1 (die eerste, linker syfer in 121) met 1 (die eerste, linker syfer in 151), wat gelyk is aan 1. Skryf die 1 onder die vermenigvuldigingslyn in die linkerkolom. 
Byvoorbeeld, wanneer 121 x 151 vermenigvuldig word, vermenigvuldig eers die 1 (die boonste linkerkolom syfer in 121) met 5 (die onderste middelste kolom syfer in 151), wat gelyk is aan 5. Dan vermenigvuldig jy 1 (die getal van die onderste linkerkolom in die 151) met 2 (die getal van die boonste middelste kolom in die 121), wat gelyk is aan 2. Voeg die oplossings 5 en 2 bymekaar en jy kry 7. Skryf 7 onder die vermenigvuldigingslyn regs van die 1 wat jy reeds onder die vermenigvuldigingslyn geskryf het. 
Byvoorbeeld, wanneer jy 121 x 151 vermenigvuldig, vermenigvuldig jy 1 (die syfer heel links) met 1 (die syfer heel regs), wat gelyk is aan 1. Vermenigvuldig dan 1 (die linkerkantste syfer onder) met 1 (die regterkantste syfer bo), wat gelyk is aan 1. Voeg hierdie oplossings bymekaar, en jy kry 2 as `n antwoord. 
Byvoorbeeld, wanneer jy 121 x 151 vermenigvuldig, sal jy 2 (die middelste syfer van 121) vermenigvuldig met 5 (die middelste syfer van 151), wat gelyk is aan 10. Voeg hierdie 10 by die 2 wat jy in die vorige stap gevind het, wat gelyk is aan 12. Aangesien 12 groter as 9 is, skryf die 2 (die regterkantste syfer van 12) in die derde plek onder die vermenigvuldigingslyn regs van die 1 en 7 wat jy reeds geskryf het. Tel dan die 1 (die syfer heel links in 12) by 7 (die syfer links onder die vermenigvuldigingslyn). Dit is hoekom jy op hierdie stadium 1, 8 en 2 onder die vermenigvuldigingslyn geskryf het. 
Byvoorbeeld, wanneer jy 121 x 151 vermenigvuldig, sal jy 2 (die middelste syfer van 121) vermenigvuldig met 1 (die regter onderste syfer van 151), wat gelyk is aan 2. Vermenigvuldig dan 1 (die regter boonste syfer van 121) met 5 (die middelste syfer van 151), wat gelyk is aan 5. Tel hierdie bymekaar, wat gelyk is aan 7. Skryf die 7 langs die 1, 8 en 2 wat jy reeds neergeskryf het. 
Byvoorbeeld, wanneer jy 121 x 151 vermenigvuldig, sal jy 1 (die regterkantste syfer van 121) vermenigvuldig met 1 (die regterkantste syfer van 151), wat gelyk is aan 1. Skryf die 1 regs van die 1, 8, 2 en 7 wat jy reeds neergeskryf het. Die antwoord op jou oorspronklike probleem van 121 x 151 is dus 18.271.
Vediese vermenigvuldiging
Inhoud
Vediese Wiskunde is `n vorm van hoofrekene wat ontwerp is om jou te help om rekenkundige vergelykings op `n eenvoudiger en vinniger manier op te los. Deur net `n paar eenvoudige tegnieke te gebruik, help Vedic Mathematics jou om komplekse vermenigvuldiging af te breek in eenvoudige vermenigvuldigings-, aftrek- en optelstappe. Met `n bietjie oefening kan jy Vediese vermenigvuldiging gebruik om beide groot en klein probleme maklik en binne sekondes op te los.
Trappe
Metode 1 van 3: Vediese vermenigvuldiging van getalle met een syfer

1. Gebruik Vediese Wiskunde om getalle groter as 5 te vermenigvuldig. As een van die getalle wat jy vermenigvuldig groter as 5 is, kan Vedic Math jou help om die vermenigvuldiging vinniger en makliker op te los. As een van die getalle egter minder as 6 is, is dit waarskynlik dat dit vinniger sal wees om die antwoord uit die geheue te herroep.
- Vediese vermenigvuldiging is ontwerp vir groter getalle. As u dus met 1, 2, 3, 4 of 5 vermenigvuldig, is dit gewoonlik baie vinniger en makliker om die probleem op te los sonder om Vediese wiskunde te gebruik.

2. Skryf die getalle neer wat jy wil vermenigvuldig. Skryf op `n stuk papier die eerste nommer van die probleem en die tweede nommer direk daaronder. Trek `n lyn onder die tweede nommer (jy sal later die oplossing vir die probleem onder hierdie lyn neerskryf).

3. Trek beide die boonste en onderste getalle van die Vediese basis 10 af. As jy die berekeninge een op `n slag doen, trek eers die boonste getal van 10 af en skryf die resultaat regs van die oorspronklike getal neer. Dan trek jy die onderste getal van 10 af en skryf dit regs van die oorspronklike getal en direk onder die nuwe berekening van die boonste getal neer. Jy het nou twee kolomme nommers, met die oorspronklike nommers in `n kolom aan die linkerkant en jou nuwe nommers in `n kolom aan die regterkant.

4. Vermenigvuldig die getalle in die regterkolom. Vermenigvuldig die boonste getal in die regterkolom met die onderste getal in die regterkolom op die gewone manier. As die antwoord op die vermenigvuldiging groter as 10 is, skryf die regterkantste syfer onder die lyn en dra die heel linkse syfer oor na die volgende stap. As die antwoord een syfer is, skryf net die een syfer antwoord onder die reël onder die regterkolom.

5. Trek `n getal van die regterkolom af van die getal in die diagonale linkerkolom. Kies die boonste of onderste nommer uit die linkerkolom (dit maak nie saak watter een jy kies nie - die oplossing sal altyd dieselfde wees). Trek dan die getal af wat diagonaal in die regterkolom is.

6. Voeg die nommer wat jy onthou het (indien van toepassing) by die resultaat. As die oplossing vir die vermenigvuldiging van die getalle in die regterkolom meer as 10 was, skryf die syfer heel regs onder die lyn van die regterkolom en dra die syfer heel links oor. Op hierdie punt, tel die onthou getal by die oplossing van die diagonale aftrekking in die vorige stap, en skryf die som onder die lyn in die linkerkolom.

7. Lees die nommer onder die reël van die probleem om die oorspronklike probleem te beantwoord. Jy het nou twee nommers onder die lyn geskryf. Hierdie getalle verteenwoordig saam `n enkele getal, wat die oplossing vir jou oorspronklike vergelyking is.
Metode 2 van 3: Vermenigvuldiging van tweesyfergetalle

1. Skryf jou vermenigvuldiging neer. Skryf op `n stuk papier die eerste getal met twee syfers van die vermenigvuldiging bo-op en die tweede getal direk daaronder. Trek `n lyn onder die tweede nommer (jy sal later die oplossing vir die probleem onder hierdie reël neerskryf).
- Byvoorbeeld, as jy Vediese wiskunde wil gebruik om 20 x 21 te vermenigvuldig, skryf 20 en 21 reg onder dit. Trek `n lyn net onder 21.
- As jy besonder bedrewe is om wiskundeprobleme in jou kop op te los, kan jy hierdie uitleg visualiseer in plaas daarvan om dit neer te skryf. Dit kan egter nuttig wees om die vermenigvuldiging neer te skryf wanneer jy eers met Vediese vermenigvuldiging begin.

2. Gebruik tradisionele vermenigvuldiging om die getalle in die linkerkolom te vermenigvuldig. Vermenigvuldig eers die boonste linker syfer van die eerste nommer met die onderste linker syfer van die tweede nommer. Skryf jou antwoord onder die vermenigvuldigingslyn, in die mees linkerkolom. Hierdie nommer is die eerste deel van die oplossing.

3. Vermenigvuldig die diagonale getalle en tel die oplossings by. Vermenigvuldig eers die nommer van die boonste linkerkolom met die nommer van die onderste regterkolom. Vermenigvuldig dan die getal in die linkerkolom met die getal in die boonste regterkantste kolom. Voeg die oplossings bymekaar en skryf die antwoord onder die vermenigvuldigingslyn regs van die oplossing in die vorige stap neer.

4. Bepaal die finale antwoord deur die getalle in die regterkolom te vermenigvuldig. Vermenigvuldig die boonste getal in die regterkolom met die getal onderaan die regterkolom. Skryf die oplossing onder die vermenigvuldigingslyn in die mees regterkantste kolom. Lees dan die getal onder die vermenigvuldigingslyn van links na regs om jou finale antwoord op die oorspronklike probleem te kry.
Metode 3 van 3: Vediese vermenigvuldiging met driesyfergetalle

1. Skryf die getalle neer wat jy vermenigvuldig. Skryf eers die eerste driesyfergetal van die vermenigvuldiging neer. Skryf dan die tweede nommer direk daaronder. Trek `n lyn onder die tweede nommer (jy sal later die oplossing vir die probleem onder hierdie reël neerskryf). Jy behoort nou drie kolomme nommers te hê.
- Byvoorbeeld, as jy Vediese wiskunde gebruik om 121 x 151 te vermenigvuldig, skryf 121 en skryf 151 direk daaronder. Trek `n lyn onder 151.
- Alhoewel jy dalk dink dat jy na `n bietjie oefening in staat sal wees om `n Vediese vermenigvuldiging uit die kop te doen, kan dit nuttig wees om die vermenigvuldiging uit te skryf wanneer jy die eerste keer begin.

2. Vermenigvuldig die getalle in die linkerkolom. Vermenigvuldig eers die boonste linker syfer van die eerste nommer, met die onderste linker syfer van die tweede nommer. Skryf jou antwoord onder die vermenigvuldigingslyn, in die mees linkerkolom. Hierdie nommer is die eerste deel van die oplossing.

3. Vermenigvuldig die getalle van die linkerkolom met die diagonale middelgetalle. Vermenigvuldig eers die boonste getal van die linkerkolom met die onderste getal van die middelste kolom. Vermenigvuldig dan die onderste getal van die linkerkolom met die boonste getal van die middelste kolom. Voeg die resultaat van hierdie twee berekeninge bymekaar. Die gevolglike getal is die tweede deel van die oplossing.

4. Vermenigvuldig die getalle heel links en regs. Vermenigvuldig eers die getal links bo met die getal regs onder. Vermenigvuldig dan die syfer heel links met die syfer heel regs. Voeg hierdie twee oplossings bymekaar en skryf die antwoord aan die kant sodat jy nie vergeet nie.

5. Tel die vermenigvuldiging van die middelste syfers by die vorige oplossing. Vermenigvuldig die boonste getal van die middelste kolom met die onderste getal van die middelste kolom. Voeg dan die oplossing by die getal wat jy in die vorige stap gevind het. As die antwoord minder as 10 is, skryf net die antwoord onder die vermenigvuldigingsreël regs van die getalle wat jy reeds neergeskryf het. As die antwoord groter as 9 is, skryf die regterkantste syfer onder die vermenigvuldigingslyn en tel die volgende linkersyfer by die getal links daarvan.

6. Beweeg na die middelste kolom om die hoeklyne in die regterkolom te vermenigvuldig. Vermenigvuldig eers die boonste getal van die middelste kolom met die onderste getal van die regterkolom. Vermenigvuldig dan die boonste getal van die regterkolom met die onderste getal van die middelste kolom. Tel hierdie getalle bymekaar en skryf die oplossing regs van die drie getalle wat jy reeds neergeskryf het neer.

7. Vermenigvuldig die getalle in die regterkolom om die oplossing te vind. Vermenigvuldig die boonste getal in die regterkolom met die onderste getal in die regterkolom. Skryf die oplossing onder die vermenigvuldigingslyn regs van die vier getalle wat jy reeds neergeskryf het, neer. As jy dan van links na regs lees, het jy die oplossing van die oorspronklike vergelyking.
Artikels oor die onderwerp "Vediese vermenigvuldiging"
Оцените, пожалуйста статью
Gewilde