Proporsieberekening: 7 stappe (met prente)

Inhoud

Trappe
- Deel 1 van 2: Skryf `n verhouding
- Deel 2 van 2: Gebruik verhoudings in wiskundeprobleme
Voorbeeld oefeninge
Wenke
Benodigdhede

Proporsies of verhoudings is wiskundige uitdrukkings wat twee of meer getalle vergelyk. Proporsies kan vaste hoeveelhede en getalle vergelyk of kan gebruik word om dele van die geheel te vergelyk. Proporsies kan op verskillende maniere bereken en aangeteken word, maar die beginsels is dieselfde vir alle verhoudings. Sien Stap 1 hieronder om met proporsies te begin.

Trappe

Deel 1 van 2: Skryf `n verhouding

Prent getiteld Bereken verhoudings Stap 1

1. Verstaan hoe proporsies gebruik word. Verhoudings word oral gevind, in die wetenskaplike wêreld of by die huis. Die eenvoudigste verhoudings vergelyk net twee waardes, maar meer is natuurlik ook moontlik.

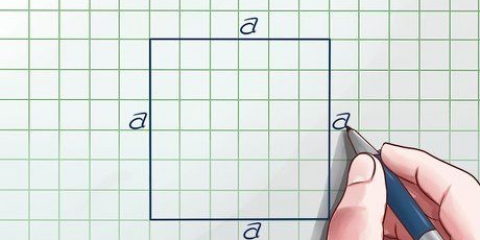
`n Voorbeeld: in `n klas met 20 studente waarvan 5 meisies en 15 seuns, kan ons die aantal meisies en seuns as `n verhouding uitdruk.

Prent getiteld Bereken verhoudings Stap 2

2. Skryf `n verhouding met `n dubbelpunt. `n Algemene manier om `n verhouding aan te dui is met `n dubbelpunt tussen die getalle. As jy twee getalle vergelyk, skryf jy dit byvoorbeeld neer as 7 : 13 en as daar 3 of meer getalle is, dan byvoorbeeld soos volg 10 : 2 : 23.

Dus, in ons klaskamer kan ons die verhouding van meisies tot seuns soos volg skryf:5 meisies: 15 seuns. Jy kan opsioneel die benaming weglaat, solank jy onthou waarvoor die verhouding staan.

Prent getiteld Bereken verhoudings Stap 3

3. `n Verhouding is dieselfde as `n breuk en kan dus vereenvoudig word. Jy doen dit deur alle terme van die verhouding deur die gemene delers te deel totdat daar nie meer gemene delers oor is nie. Maar wanneer jy dit doen, is dit belangrik om nie te vergeet wat die oorspronklike getalle van die verhouding was nie. Sien onder.

In die klaskamervoorbeeld was daar 5 meisies en 15 seuns. Albei kante van die verhouding is deelbaar deur 5. Dit laat jou toe om die verhouding te vereenvoudig1 meisie: 3 seuns.

Maar ons moet nie die oorspronklike getalle uit die oog verloor nie. Daar is nie 4 nie maar 20 studente in totaal in die klas. Die vereenvoudigde verhouding vergelyk slegs die verhouding tussen die aantal seuns en meisies. Daar is 3 seuns tot 1 meisie in die verhouding of breuk, nie 3 seuns en 1 meisie in die klas nie.

Sommige verhoudings kan nie vereenvoudig word nie. Byvoorbeeld, 3 : 56 kan nie vereenvoudig word nie omdat die 2 getalle geen gelyke faktore het nie - 3 is priem en 56 is nie deelbaar deur 3.

4. Daar is ook alternatiewe metodes om proporsies te skryf. Alhoewel die dubbelpunt miskien die maklikste is om verhoudings te skryf, is daar ander maniere wat nie die verhouding beïnvloed nie. Sien onder:

Proporsies kan ook vertoon word as "3 staan tot 6" of "11 op 4 op 20".

Jy kan ook proporsies as `n breuk skryf. Dikwels lei die gebruik van beide terme tot `n mate van verwarring, maar breuke is proporsies en omgekeerd. Jy kan dus ook `n verhouding met `n deellyn skryf. Byvoorbeeld, die verhouding 3/5 en die breuk 3/5 nie van mekaar verskil nie. Soos in die voorbeeld van die klas: daar was 3 seuns vir elke meisie, `n verhouding van 1 : 3, maar as `n breuk dieselfde ding uitdruk, naamlik 1/3 van die totale aantal studente is `n meisie.

Deel 2 van 2: Gebruik verhoudings in wiskundeprobleme

1. Gebruik vermenigvuldiging of deling om verhoudings te verander sonder om die verhouding te verander. Vermenigvuldiging of deling van beide terme van `n verhouding deur `n gegewe getal produseer dieselfde verhouding, maar met groter of kleiner getalle.

Gestel byvoorbeeld jy is `n onderwyser en jy word gevra om die grootte van die klas 5 keer te vergroot, maar met dieselfde verhouding van seuns en meisies. As daar nou 8 meisies en 11 seuns in die klas is, hoeveel is in die nuwe klas?Lees verder vir die oplossing:

8 meisies en 11 seuns, dus `n verhouding van 8:11. Hierdie verhouding dui dus aan dat, ongeag die grootte van die klas, daar 8 meisies tot 11 seuns is.
(8 : 11) × 5
(8×5: 11×5)
(40:55). Die nuwe klas bestaan uit 40 meisies en 55 ouens - 95 studente in totaal!

Prent getiteld Bereken verhoudings Stap 4

2. Gebruik kruisvermenigvuldiging om die onbekende veranderlike te vind wanneer jy met twee ekwivalente verhoudings werk. Nog `n bekende probleem is dat waar jy gevra word om die onbekende van `n verhouding te bereken. Kruisvermenigvuldiging maak dit baie maklik om dit uit te werk. Skryf elke verhouding as `n breuk, maak hulle gelyk en vermenigvuldig kruisgewys om op te los.

As `n voorbeeld, kom ons sê ons het `n groep studente van 2 seuns en 5 meisies. As ons die verhouding ongeskonde wil hou, hoeveel seuns is daar in `n groep van 20 meisies?Om dit op te los maak ons twee verhoudings, een met die onbekende veranderlike: 2 seuns : 5 meisies = x seuns : 20 meisies. In breukvorm lyk dit so: 2/5 = x/20. Gebruik kruisvermenigvuldiging om dit op te los. Sien onder:

2/5 = x/20

5 × x = 2 × 20

5x = 40

x = 40/5 = 8. So daar is 20 meisies en 8 ouens.

3. Gebruik verhoudings om onbekende hoeveelhede te vind, waar `n ander gegee word. As jy te doen het met `n veranderlike wat die verband tussen verskeie hoeveelhede bepaal, waarvan 1 of meer onbekend is, kan jy die waarde van elke onbekende vind deur slegs een bekende grootheid te gebruik. Dikwels behels hierdie tipe stellings die berekening van die hoeveelhede bestanddele in `n resep. Om die onbekende hoeveelhede te vind, deel die bekende term van die verhouding deur die gegewe hoeveelheid; deel daarna elke term in die verhouding deur die antwoord wat jy kry. `n Voorbeeld sal dit alles `n bietjie duideliker maak:

Gestel ons klas bak koekies as `n opdrag. As die deegresep uit meel, water en botter in die verhouding 20 : 8 : 4 bestaan, en elke student kry 5 koppies meel; hoeveel water en botter het elke student nodig? Om dit op te los, deel eers die term van die verhouding wat ooreenstem met die bekende verhouding (20) deur die bekende hoeveelheid (5 koppies). Deel dan elke term in die verhouding deur die antwoord wat jy kry om die presiese bedrag vir elkeen te vind. Sien onder:

20/5 = 4

20/4 : 8/4 : 4/4

5 : 2 : 1. Dus, 5 koppies meel, 2 koppies water en 1 koppie botter.

Voorbeeld oefeninge

Koekies word gemaak van botter en suiker in `n verhouding van 5:3. As 7 dele botter gebruik word, hoeveel suiker is nodig?

Om dit te doen, gebruik die verhouding in die vorm van `n breuk. In hierdie geval maak ons dit `n desimale - ongeveer 1,67.
Die formule is nou gereed om te gebruik. Ons wil die hoeveelheid suiker vind, so kom ons laat dit vir wat dit is en bereken die breuk botter/1.67, dus 7/1.67 = 4.192

Die deel wat oor proporsies handel, is proporsionele verdeling. Wanneer `n totale hoeveelheid in dele verdeel word, word `n verhouding geskep. Byvoorbeeld: Annemiek, Anna en Anton werk almal in hul ma se winkel. Annemiek het een uur gewerk, Anna 3 en Anton 6 uur (dus `n verhouding 1:3:6). Ma gee vir hulle `n totale bedrag en vra hulle om dit self in die regte verhouding te verdeel. Die totale bedrag was €100. Jy doen dit deur die dele van die verhouding bymekaar te tel, sodat jy weet hoeveel elke deel werd is. 1:3:6 word dan 1+3+6=10 so $100/10=$10 so ons weet nou dat elke deel van die verhouding $10 werd is... en daarom kry almal `n loon van €10 per uur. Nou kan ons dit gebruik om te bereken wat elkeen verdien het. Annemiek kry €10, Anna kry €30 en Anton kry €60. Kontroleer dit deur al die lone by te tel, wat op €100 behoort uit te kom. 10+30+60= 100. Korrek!

Wenke

Vereenvoudig verhoudings deur die ab/c-knoppie op jou sakrekenaar te gebruik (dit is vir die skryf van gemengde breuke en vereenvoudiging). Byvoorbeeld, as jy 8:12 het, toets jy "8 ab/c 12" = in en jy kry 2/3, en dus die verhouding 2:3.