Hoe om 'n logaritmiese skaal te lees: 10 stappe (met prente)

Inhoud

Trappe
- Metode 1 van 2: Lees die asse van die grafiek
- Metode 2 van 2: Teken punte op `n logaritmiese skaal
Waarskuwings

Die meeste mense is vertroud met die lees van getalle op `n getallelyn of die lees van data vanaf `n grafiek. Onder sekere omstandighede is `n standaardskaal egter nie bruikbaar nie. As die data eksponensieel groei of afneem, dan moet jy `n sogenaamde logaritmiese skaal gebruik. Byvoorbeeld, `n grafiek van die aantal McDonald`s-hamburgers wat oor tyd verkoop is, sou in 1955 by 1 miljoen begin; as 5 miljoen net `n jaar later, dan 400 miljoen, 1 miljard (in minder as 10 jaar) en tot 80 miljard in 1990. Hierdie data sal te veel wees vir `n standaardgrafiek, maar kan maklik op `n logaritmiese skaal voorgestel word. Weet dat `n logaritmiese skaal `n ander stelsel het om die getalle voor te stel, wat nie eweredig versprei is soos op `n standaardskaal nie. Om te weet hoe om `n logaritmiese skaal te lees, sal jou help om die data meer effektief te lees en dit grafies te vertoon.

Trappe

Metode 1 van 2: Lees die asse van die grafiek

Prent getiteld Lees `n logaritmiese skaal Stap 1

1. Bepaal of een of albei asse `n logskaal gebruik. Grafieke wat vinnig groeiende data vertoon, kan asse met een of twee logskale gebruik. Die verskil lê daarin of beide die x-as en y-as logaritmiese skale gebruik, of net een. Die keuse hang af van hoeveel detail jy met die grafiek wil wys. As getalle op die een of die ander as eksponensieel groei of afneem, wil jy dalk `n logaritmiese skaal vir daardie as gebruik.

`n Logaritmiese (of net `log`) skaal het ongelyke roosterlyne. `n Standaardskaal het eweredig gespasieerde roosterlyne. Sommige data moet slegs op standaardpapier geteken word, ander op semi-log-grafieke, en nog ander op log-log-grafieke.
Byvoorbeeld: Die grafiek van $y = \sqrt{X}$ ${displaystyle y={sqrt {x}}}$ (of `n soortgelyke funksie met `n vierkantswortelterm) kan op `n standaardgrafiek, `n semi-log-grafiek of `n log-log-grafiek geplot word. In `n standaardgrafiek is die funksie `n sywaartse parabool, maar die detail vir baie klein getalle is moeilik om te sien. As `n log-log grafiek is dieselfde funksie `n reguit lyn en die waardes is meer versprei, vir meer besonderhede.
As beide veranderlikes in `n studie groot hoeveelhede data bevat, sal jy waarskynlik `n log-log grafiek gebruik. Studies oor evolusionêre effekte, byvoorbeeld, kan oor duisende of miljoene jare gemeet word waar `n logaritmiese skaal vir die x-as gepas kan wees. Afhangende van die item wat gemeet moet word, kan `n log-log skaal vereis word.

Prent getiteld Lees `n logaritmiese skaal Stap 2

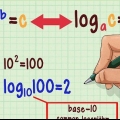
2. Lees die hoofafdelingskaal. Op `n logaritmiese skaalgrafiek verteenwoordig die eweredig gespasieerde merkers die magte van die basis waarmee jy werk. Die standaard logaritmes gebruik óf die basis 10 óf die natuurlike logaritme met

e

$e$ as basis.

e

$e$ is `n wiskundige konstante wat nuttig is wanneer met saamgestelde rente en ander gevorderde berekeninge gewerk word. Dit is ongeveer gelyk aan 2,718. Hierdie artikel sal fokus op basis 10 logaritmes, maar die natuurlike logaritme skaallesing werk op dieselfde manier.

Standaardlogaritmes het basis 10 as basis. In plaas van 1, 2, 3, 4... of 10, 20, 30, 40... of enige ander eweredige skaal, tel `n logaritmeskaal met magte van 10. Die hoofaspunte is dus,

101, 10^{2}, 10^{3}, 10^{4}

${displaystyle 10^{1},10^{2},10^{3},10^{4}}$ ens.

Elkeen van die hoofafdelings, gewoonlik met `n donkerder lyn op houtpapier gemerk, word `n `siklus` genoem. As jy spesifiek die basis 10 gebruik, kan jy die term "dekade" gebruik, want dit verwys na `n nuwe krag van 10.

Prent getiteld Lees `n logaritmiese skaal Stap 3

3. Let daarop dat klein intervalle nie eweredig versprei is nie. As jy logaritmiese grafiekpapier gebruik, sal jy agterkom dat die intervalle tussen die hooftoestelle nie eweredig versprei is nie. Dit wil sê, byvoorbeeld, die merker vir 20 sal eintlik ongeveer 1/3 van die afstand tussen 10 en 100 geplaas word.

Die klein intervalle is gebaseer op die logaritme van elke getal. As 10 dus as die eerste hoofpunt op die skaal voorgestel word en 100 as die tweede, val die ander getalle soos volg tussenin:

l O g (10) = 1

${displaystyle log(10)=1}$

l O g (20) = 1, 3

${displaystyle log(20)=1.3}$

l O g (30) = 1, 48

${displaystyle log(30)=1.48}$

l O g (40) = 1, 60

${displaystyle log(40)=1.60}$

l O g (50) = 1, 70

${displaystyle log(50)=1.70}$

l O g (60) = 1, 78

${displaystyle log(60)=1.78}$

l O g (70) = 1, 85

${displaystyle log(70)=1.85}$

l O g (80) = 1, 90

${displaystyle log(80)=1.90}$

l O g (90) = 1, 95

${displaystyle log(90)=1.95}$

l O g (100) = 2, 00

${displaystyle log(100)=2.00}$

By hoër magte van 10 word die klein intervalle in dieselfde verhoudings versprei. Byvoorbeeld, die afstand tussen 10, 20, 30... op die afstand tussen 100, 200, 300... of 1000, 2000, 3000...

Metode 2 van 2: Teken punte op `n logaritmiese skaal

Prent getiteld Lees `n logaritmiese skaal Stap 4

1. Bepaal die tipe skaal wat jy wil gebruik. Vir die verduideliking hieronder sal die fokus op `n semi-log-grafiek wees, met `n standaardskaal vir die x-as en `n log-skaal vir die y-as. U kan dit egter omkeer, afhangende van hoe u die data wil vertoon. Om die asse om te keer het die effek dat die grafiek negentig grade verskuif en kan die data makliker maak om in die een of die ander rigting te interpreteer. Boonop wil u dalk `n logskaal gebruik om sekere datawaardes uit te versprei en hul besonderhede meer sigbaar te maak.

Prent getiteld Lees `n logaritmiese skaal Stap 5

2. Merk die skaal van die x-as. Die x-as is die onafhanklike veranderlike. Die onafhanklike veranderlike is die veranderlike wat jy gewoonlik in `n meting of eksperiment beheer. Die onafhanklike veranderlike word nie deur die ander veranderlike in die studie beïnvloed nie. Enkele voorbeelde van onafhanklike veranderlikes is:

Datum

Tyd

Ouderdom

Medikasie gegee

Prent getiteld Lees `n logaritmiese skaal Stap 6

3. Bepaal dat jy `n logaritmiese skaal vir die y-as benodig. Jy sal `n logaritmiese skaal gebruik om data wat uiters vinnig verander te karteer. `n Standaardgrafiek is nuttig vir data wat lineêr groei of daal. `n Logaritmiese grafiek is vir data wat eksponensieel verander. Voorbeelde van sulke data is:

Bevolkingsgroei

Verbruik

Saamgestelde rente

Prent getiteld Lees `n logaritmiese skaal Stap 7

4. Benoem die logaritmiese skaal. Hersien jou data en besluit hoe om die y-as te merk. As jou data slegs getalle meet binne byvoorbeeld die miljoene en biljoene, dan hoef jy waarskynlik nie die grafiek by nul te begin nie. Jy kan die laagste siklus op die grafiek benoem as

106

${displaystyle 10^{6}}$ . Volgende siklusse sal dan wees

107, 10^{8}, 10^{9}

${displaystyle 10^{7},10^{8},10^{9}}$ ens.

Prent getiteld Lees `n logaritmiese skaal Stap 8

5. Vind die posisie op die x-as vir `n datapunt. Om die eerste (of enige) datapunt te teken, begin deur sy posisie langs die x-as te bepaal. Dit kan `n stygende skaal wees, soos `n gereelde getallelyn 1, 2, 3, ens. Dit kan `n skaal van etikette wees wat jy toeken, soos datums of maande van die jaar waarin jy sekere metings neem.

Prent getiteld Lees `n logaritmiese skaal Stap 9

6. Bepaal die posisie langs die logaritmiese y-as. Jy moet die ooreenstemmende posisie langs die y-as vind vir die data wat jy wil plot. Onthou, aangesien jy met `n logaritmiese skaal werk, is die hoofpunte magte van 10 en die klein punte tussenin is die onderafdelings. Byvoorbeeld: tussen

106

${displaystyle 10^{6}}$ (een miljoen) en

107

$10^{7}$ (tien miljoen), verteenwoordig die merke stappe van een miljoen.

Byvoorbeeld: Die getal 4.000.000 sal by die vierde klein punt hierbo geplot word

106

${displaystyle 10^{6}}$ . Alhoewel 4.000.000 op `n standaard lineêre skaal minder as halfpad tussen 1.000.000 en 10.000.000, as gevolg van die logaritmiese skaal lyk dit eintlik na `n bietjie meer as halfpad.

Jy moet in gedagte hou dat die hoër intervalle, nader aan die boonste limiet, gedruk word. Dit is as gevolg van die wiskundige aard van die logaritmiese skaal.

Prent getiteld Lees `n logaritmiese skaal Stap 10

7. Gaan voort met alle data. Gaan voort om die vorige stappe te herhaal vir al die data wat jy nodig het om `n grafiek te skep. Vir elke datapunt, vind eers sy posisie langs die x-as en dan sy ooreenstemmende posisie langs die logaritmiese skaal van die y-as.

Waarskuwings

As jy data vanaf `n logaritmiese skaal lees, maak seker jy weet watter basis vir die logaritme gebruik word. Data gemeet in basis 10 sal baie verskil van data gemeet op `n natuurlike logaritmiese skaal met basis e.