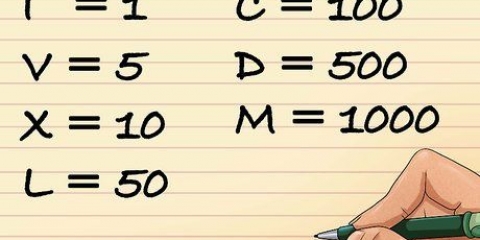Help jou kind om byvoeging te leer

Inhoud

Trappe

Om jou kind te help om toevoeging te leer, sal hom of haar goed voorberei vir skoollesse. Die meeste skole het standaarde so dat alle graadeerstes tot 20 moet kan optel en aftrek. Voordat kinders egter optel en aftrek kan bemeester, sal hulle `n goeie begrip moet hê van wat "optelling" beteken. Daar is `n verskeidenheid leerbronne om jou kind of jou klas te help om byvoeging effektief te leer, so dit is ook pret.

Trappe

Metode 1 van 4: Gebruik van voorwerpe

Prent getiteld Teach a Child Addition Stap 1

1. Gebruik voorwerpe om te wys hoe optel werk. Kinders reageer goed op visuele hulpmiddels om basiese telkonsepte te verstaan. Jy kan enige voorwerp gebruik wat maklik is om te hanteer, van krale en blokke tot munte. Begin met `n klein aantal voorwerpe en gebruik verskeie taktieke om verwantskappe tussen getalle te wys:

Gee die kind twee groepe voorwerpe – soos `n groep van twee blokke en `n groep van drie blokke. Laat die kind die aantal blokkies in elke groep tel.
Vra die kind om hierdie twee groepe voorwerpe bymekaar te sit en die totale aantal blokkies te tel. Verduidelik dat hy of sy hierdie groepe `optel` het.
Gee `n sekere aantal items – byvoorbeeld ses munte – en vra jou kind hoeveel maniere hulle die munte in ses groepe kan verdeel. Die kind kan byvoorbeeld `n groep van vyf munte maak, en `n groep van een.
Demonstreer hoe om `n groep voorwerpe te `byvoeg` deur te stapel. Begin byvoorbeeld met `n stapel van drie munte en sit nog twee op die stapel. Vra jou kind om te tel hoeveel munte nou op die stapel is.

Prent getiteld Leer `n kind byvoeging Stap 2

2. Maak groepe kinders sodat hulle self kan `tel`. In `n klaskamer-omgewing, ontgin jong kinders se behoefte om te beweeg deur hulle mekaar te laat tel. Gebruik taktieke soortgelyk aan dié wat jy sou met items, en sluit aan by groepe studente en laat hulle hulself in verskillende samestellings tel. (Dit word nie aanbeveel om studente op te stapel nie!)

Prent getiteld Teach a Child Addition Stap 3

3. Oorweeg dit om kinders hul eie voorwerpe te laat maak. Gebruik modelleerklei om voorwerpe te maak, of kombineer jou byvoegles met `n kunsles deur verskeie papiervorms te maak.

Prent getiteld Leer `n kind byvoeging Stap 4

4. Gebruik speletjies op nuwe maniere om telspeletjies te maak. Dobbelsteen leen hulself maklik tot eerste tel speletjies. Laat die studente twee dobbelstene gooi en oefen om die getalle wat gegooi word by te tel. Jy kan ook met speelkaarte of domino`s werk.

Wanneer jy met studente werk wat verskillende grade van telvaardighede het, kan jy hierdie speletjie aanpas om `n ekstra uitdaging vir vinnige leerders te skep. Gee hulle opdrag om die resultate van drie of meer dobbelstene of speelkaarte bymekaar te tel.

Prent getiteld Leer `n kind byvoeging Stap 5

5. Tel met munte. Gebruik geld om te oefen om eenhede, vyfte, tiene en selfs 25 intervalle by te voeg. Hierdie taktiek leer geldvaardighede bykomend tot telvaardighede, en het die bykomende voordeel dat dit die praktiese voordele van tel demonstreer.

Metode 2 van 4: Wiskundetaal en `somverhoudings`

Prent getiteld Leer `n kind byvoeging Stap 6

1. Stel kinders bekend aan optelsimbole. Leer hulle die betekenis van die simbole `+` en `=`. Help hulle dan om eenvoudige `berekeningsinne` te skryf, soos `3 + 2=5`.

Begin met horisontale somme. Jong kinders leer reeds dat daar van hulle verwag word om woorde en sinne `op` die papier te skryf. Om met rekenkundige sinne volgens `n soortgelyke praktyk te werk, sal dan minder verwarrend wees. Sodra kinders hierdie konsep bemeester het, kan jy begin om die konsep van vertikale somme bekend te stel.

Prent getiteld Teach a Child Addition Stap 7

2. Leer kinders die woorde soos `toevoeging`. Stel terme soos "saam", "optel", "totaal" en "som" bekend wat dikwels aandui dat `n kind twee of meer getalle bymekaar moet tel.

Prent getiteld Leer `n kind byvoeging Stap 8

3. Gebruik `somverhoudings` om kinders te help om somverhoudings te verstaan. Somrelasies wys hoe die verskillende getalle in `n optelsom met mekaar verband hou. Somverhoudings behels dikwels beide optelling en aftrekking om studente te help om die omgekeerde verband tussen hierdie twee vaardighede te verstaan. Byvoorbeeld, die heelgetalle van 4, 5 en 9 is `n `somrelasie`, want 4 + 5=9; 5 + 4=9; 9 - 4=5; en 9-5=4.

Gebruik melkkartonne om `somverhoudings` te illustreer. Draai melkkartonne toe in papier of `n maklik-om-skoonmaakbare oppervlak as jy die kartonne wil hergebruik. Laat studente die heelgetalle van `n somverhouding bo-op die karton lys – byvoorbeeld 4, 5 en 9. Laat hulle dan elke getal van so `n somverhouding op elk van die vier kante van die boks skryf.

Metode 3 van 4: Leer basiese feite

Prent getiteld Leer `n kind byvoeging Stap 9

1. Leer kinders om in `groter stappe` te tel. Leer hulle om in pare, vyfte en tiene tot 100 te tel om jou kind se begrip van getalverwantskappe te verbeter en maklike verwysingspunte te verskaf.

Prent getiteld Teach a Child Addition Stap 10

2. Moedig kinders aan om `dubbels` te onthou. `Dubbel` is somverhoudings soos `3 + 3=6` of `8 + 8=16`. Weereens, hierdie feite bied `n maklike verwysing wanneer studente leer om by te voeg. Byvoorbeeld, `n kind wat outomaties weet dat `8 + 8=16` die som van `8 + 9` kan uitvind bloot deur 1 by die totaal te tel.

Prent getiteld Leer `n kind byvoeging Stap 11

3. Gebruik flitskaarte om memorisering aan te moedig. Groepeer kaarte volgens somverhouding om die verband tussen hierdie getalle te beklemtoon. Terwyl studente in staat moet wees om te herken hoe getalle interaksie het, sal die memorisering van basiese wiskundefeite `n bykomende grondslag bied om na meer komplekse somme aan te beweeg.

Metode 4 van 4: Gebruik probleme

Prent getiteld Leer `n kind byvoeging Stap 12

1. Oefen verskillende tipes probleme. Terwyl sommige studente kwessies meer kompleks vind, sal ander floreer namate hulle `n beter begrip kry van hoe om toevoeging in die werklike wêreld toe te pas. Help jou kind om drie verskillende situasies te identifiseer wat byvoeging vereis:

Soms met `n `onbekende resultaat` – Byvoorbeeld: as Merel twee motors het en nog drie op haar verjaardag kry, hoeveel motors het sy altesaam??
Somme met `n `onbekende verandering` – Byvoorbeeld: as "Merel het twee karre en ná haar verjaardag vyf karre, hoeveel karre het sy vir haar verjaardag gekry?
Soms met `n `onbekende beginpunt` – Byvoorbeeld, as Merel drie karre vir haar verjaardag kry en nou vyf het, hoeveel motors moes sy mee begin?

Prent getiteld Leer `n kind byvoeging Stap 13

2. Leer kinders om `samesmelt`, `deel-deel-geheel` en `vergelyk` probleme te herken. Werklike situasies behels verskillende parameters. Om te verstaan hoe hierdie werk jou kind sal help om probleemoplossingsinstrumente te ontwikkel.

`Saamvoeg`-probleme verwys na die groei van `n gegewe hoeveelheid. Byvoorbeeld, as Elizabeth drie koeke bak en Sara bak nog ses, hoeveel koeke is daar altesaam?? Samevoegprobleme kan studente ook vra om vir `n onbekende verandering of beginnommer op te los -- byvoorbeeld, as Elizabeth drie koeke bak en Elizabeth en Sara maak nege koeke saam, hoeveel koeke het Sara gebak??

`Deel-deel-geheel`-probleme gaan oor die byvoeging van twee vaste getalle. Byvoorbeeld, as daar 12 meisies in die klas en 10 seuns is, hoeveel studente is daar in totaal in die klas?

`Vergelyk` probleme hou verband met `n onbekende in `n stel vergelykende waardes. Byvoorbeeld, as Geert sewe koekies het en hy het drie koekies meer as Laura, hoeveel koekies het Laura?

Prent getiteld Leer `n kind byvoeging Stap 14

3. Gebruik boeke wat optelkonsepte leer. Kinders wat dit geniet om te lees en skryf, kan veral baat by boeke wat oor byvoegingstemas handel. Doen navorsing oor `leer om met stories te tel` aanlyn vir `n oorsig van nuttige literatuur, saamgestel deur onderwysers.