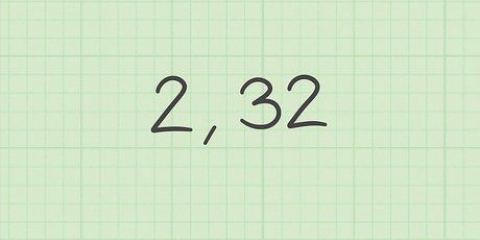Let daarop dat elke uitkoms $10 laer is as hierbo beskryf, aangesien jy eers $10 per wedstryd moet betaal, ongeag die uitslag. 
Jou 1/6 sakrekenaar maak dalk iets soos 0,166667. Ons sal dit afrond tot 0,167 om dit makliker te maak om mee te bereken, sonder om akkuraatheid in te boet. As jy `n baie akkurate resultaat wil hê, moet dit nie na desimale omskakel nie, voer net 1/6 in die formule in en bereken dit so op jou sakrekenaar. 
Dit is nie nodig om hierdie resultate nou te bereken as jy `n sakrekenaar het wat verskeie bewerkings gelyktydig kan uitvoer nie. Jy sal `n meer akkurate resultaat kry as jy die hele vergelyking invoer. 

Hoe meer dikwels `n situasie herhaal word, hoe meer akkuraat is die verwagtingswaarde `n voorstelling van die werklike, gemiddelde uitkoms. Byvoorbeeld, jy kan die speletjie 5 keer in `n ry speel en elke keer verloor, wat `n gemiddelde verlies van € 10 tot gevolg het. As jy egter die speletjie nog 1000 keer speel, sal die gemiddelde resultaat nader en nader aan die verwagte waarde van -€1,67 per wedstryd kom. Hierdie beginsel word genoem "die wet van groot getalle." 

x = ____ 
x = (0.5)(x+1) + ___ Ons gaan die leë spasie vul terwyl ons aanhou dink oor ander situasies. Jy kan breuke in plaas van desimale gebruik as dit makliker of nodig is. 
As die tweede gooi munt is, dan is ons terug by die begin. As die tweede keer ook `n koppie is, dan is ons klaar! 

x = (0.5)(x+1) + (0.25)(x+2) + ___ 
x = (0.5)(x+1) + (0.25)(x+2) + (0.25)(2) As jy nie seker is dat jy deur elke moontlike situasie gedink het nie, is daar `n maklike manier om te kyk of die vergelyking volledig is. Die eerste getal in elke deel van die vergelyking verteenwoordig die waarskynlikheid dat `n gebeurtenis sal plaasvind. Dit sal altyd 1 optel. Hier is 0.5 + 0.25 + 0.25 = 1, so ons weet dat ons elke situasie ingesluit het. 
x = 0.5x + (0.5)(1) + 0.25x + (0.25)(2) + (0.25)(2) x = 0,5x + 0,5 + 0,25x + 0,5 + 0,5 x = 0,75x + 1,5 
x = 0,75x + 1,5 x - 0,75x = 0,75x + 1,5 - 0,75x 0,25x = 1,5 (0.25x)/(0.25) = (1.5)/(0.25) x = 6 Jy sal gemiddeld 6 keer `n muntstuk moet gooi voordat jy twee keer koppe gooi. 

Die oortuiging dat jy gelukkig of ongelukkig kan wees wanneer jy munte gooi (of enige ander kansspeletjie), of dat al jou slegte geluk nou verby is en geluk aan jou kant sal wees, word ook dobbelaars-droging (of die dobbelaar se drogredenis) genoem. Dit het te doen met mense se neiging om riskante of dom besluite te neem wanneer hulle voel dat geluk aan hulle kant is, of dat hulle "gelukkige streep" of as hulle hul voel "geluk is op die punt om te draai." 
Berekening van die verwagte waarde
Inhoud
Verwagting is `n statistiese term, en `n konsep wat gebruik word om te besluit hoe nuttig of skadelik `n aksie sal wees. Om die verwagtingswaarde te bereken, is dit nodig om `n goeie begrip te verkry van elke uitkoms in `n gegewe situasie en die gepaardgaande waarskynlikheid daarvan, dit wil sê die waarskynlikheid dat `n bepaalde uitkoms sal plaasvind. Die stappe hieronder verskaf `n paar voorbeeldoefeninge om jou te help om die konsep van die verwagtingswaarde te verstaan.
Trappe
Metode 1 van 3: `n Eerste eenvoudige probleem

1. Lees die opdrag. Voordat jy aan alle moontlike uitkomste en waarskynlikhede begin dink, is dit belangrik dat jy die probleem goed verstaan. Byvoorbeeld, `n dobbelsteenspeletjie wat €10 per wedstryd kos. `n 6-kant dobbelsteen word een keer gerol en jou winste hang af van die nommer wat jy gooi. As `n 6 gerol word, wen jy €30; `n 5 gee jou $20; enige ander getal lewer niks op nie.

2. Lys alle moontlike uitkomste. Dit help om alle moontlike uitkomste in `n gegewe situasie te lys. In die voorbeeld hierbo is daar 6 moontlike uitkomste. Dit is: (1) rol `n 1 en jy verloor $10, (2) rol `n 2 en jy verloor $10, (3) rol `n 3 en jy verloor $10, (4) rol `n 4 en jy verloor $10, (5) rol `n 5 en wen €10, (6) rol `n 6 en wen €20.

3. Bepaal die waarskynlikheid van elke uitkoms. In hierdie geval is die waarskynlikheid van enige 6 uitkomste dieselfde. Die waarskynlikheid om `n ewekansige getal te laat rol is 1 uit 6. Om dit makliker te maak om neer te skryf, skryf ons die breuk (1/6) as `n desimale met `n sakrekenaar: 0.167. Skryf hierdie waarskynlikheid langs elke uitkoms neer, veral as jy `n probleem met verskillende waarskynlikhede vir elke uitkoms wil oplos.

4. Teken die waarde van elke uitkoms aan. Vermenigvuldig die aantal € van `n resultaat met die waarskynlikheid dat daardie resultaat sal plaasvind om te bereken hoeveel geld daardie resultaat tot die verwagte waarde bydra. Byvoorbeeld, die resultaat om `n 1 te rol is -$10 en die waarskynlikheid om `n 1 te rol is 0,167. Die waarde om `n 1 te rol is dus (-10) * (0.167).

5. Tel die waarde van elke uitkoms bymekaar om die verwagte waarde van `n gebeurtenis te kry. Om voort te gaan met die voorbeeld hierbo, is die verwagtingswaarde van die dobbelsteenspel: (-10 *0.167) + (-10 *0.167) + (-10 *0.167) + (-10 *0.167) + (10 *0.167) + (20 *0,167), of - €1,67. So jy kan verwag om elke keer $1,67 te verloor op hierdie speletjie (per wedstryd).

6. Wat is die implikasies van die berekening van die verwagtingswaarde. In die voorbeeld hierbo het ons vasgestel dat die verwagte wins (verlies) - $1,67 per rol sou wees. Dit is `n onmoontlike uitkoms vir 1 wedstryd; jy kan €10 verloor, €10 wen of €20 wen. Maar op die lang termyn is die verwagtingswaarde `n nuttige, gemiddelde waarskynlikheid. As jy aanhou om hierdie speletjie te speel, sal jy gemiddeld sowat $1,67 per wedstryd verloor. Nog `n manier om oor verwagtingswaarde te dink, is deur sekere koste (of voordele) aan die spel toe te ken; jy moet hierdie speletjie net speel as jy dink dit is die moeite werd, hou daarvan genoeg om elke keer $1,67 te spandeer.
Metode 2 van 3: Bereken die verwagte waarde vir `n spesifieke resultaat

1. Gebruik hierdie metode om die gemiddelde aantal munte te bereken wat jy moet omdraai voordat `n sekere patroon voorkom. Byvoorbeeld, jy kan die metode gebruik om die verwagte aantal munte uit te vind om te draai totdat jy koppe twee keer in `n ry slaan. Hierdie probleem is `n bietjie moeiliker as `n standaard verwagting waarde probleem, so as jy nie vertroud is met die verwagting waarde, lees eers die bogenoemde deel van hierdie artikel.

2. Gestel ons soek `n waarde x. Jy probeer vasstel hoeveel munte jy gemiddeld moet omslaan om koppe twee keer in `n ry te kry. Ons maak nou `n vergelyking om die antwoord te vind. Ons noem die antwoord waarna ons soek x. Ons maak die nodige vergelyking stap vir stap. Ons het tans die volgende:

3. Dink aan wat gebeur wanneer die eerste flip betaal.In die helfte van die gevalle sal dit die geval wees. As dit die geval is, dan moet jy omdraai "vermors", terwyl die waarskynlikheid om twee koppe in `n ry te slaan nie verander het nie. Soos met die muntgooi, word daar verwag dat jy `n gemiddelde aantal kere sal moet gooi om twee koppe in `n ry te kry. Met ander woorde, jy moet verwag om `n x aantal kere te rol, plus die wat jy reeds gedraai het. In die vorm van `n vergelyking:

4. Dink aan wat gebeur as jy jou kop gooi. Daar is `n 0,5 (of 1/2) kans dat jy die eerste keer `n koppie sal rol. Dit lyk asof dit nader aan die doelwit kom om twee keer in `n ry `n kop te gooi, maar hoeveel? Die maklikste manier om uit te vind is om te dink oor jou opsies op die tweede rol:

5. Leer hoe om die waarskynlikheid te bereken dat twee gebeurtenisse albei sal plaasvind. Ons weet nou dat jy `n 50% kans het om `n kop te slaan, maar wat is die waarskynlikheid om `n kop twee keer in `n ry te rol?? Om hierdie waarskynlikheid te bereken, vermenigvuldig die waarskynlikheid van albei saam. In hierdie geval is dit 0,5 x 0,5 = 0,25. Dit is natuurlik ook die waarskynlikheid dat jy eers koppe en dan sterte gooi, want albei het `n waarskynlikheid van 0.5 om voor te kom: 0.5 x 0.5 = 0.25.

6. Tel die resultaat by vir "koppe, dan sterte" by die vergelyking. Noudat ons die waarskynlikheid bereken het dat hierdie gebeurtenis sal plaasvind, kan ons voortgaan met die uitbreiding van die vergelyking. Daar is `n 0.25 (of 1/4) kans dat ons twee gooie sal mors sonder om `n stap verder te kom. Maar nou het ons gemiddeld nog x getal meer gooie nodig om die resultaat te kry wat ons wil hê, plus die 2 wat ons reeds gerol het. In die vorm van `n vergelyking word dit (0.25)(x+2), wat ons nou by die vergelyking kan voeg:

7. Voorvoegsel die resultaat "kop kop" voeg by die vergelyking. As jy koppe gooi met die eerste twee gooie van die munte, is jy klaar. Jy het die resultaat in presies 2 gooie gekry. Soos ons vroeër vasgestel het, is daar `n 0.25 kans dat dit sal gebeur, so die vergelyking hiervoor is (0.25)(2). Ons vergelyking is nou voltooi:

8. Vereenvoudig die vergelyking. Kom ons vereenvoudig die vergelyking deur te vermenigvuldig. Onthou, as jy iets tussen hakies soos hierdie sien: (0.5)(x+1), dan vermenigvuldig jy 0.5 met elke term binne die tweede stel hakies. Dit gee jou die volgende: 0.5x + (0.5)(1), of 0,5x + 0,5. Kom ons doen dit vir elke term in die vergelyking, en kombineer dan daardie terme om dinge `n bietjie eenvoudiger te laat lyk:

9. Los op vir x. Soos in enige vergelyking sal jy die x aan die een kant van die vergelyking moet isoleer om dit te bereken. Onthou dat x dieselfde beteken as "die gemiddelde aantal munte wat jy moet gooi om koppe twee keer in `n ry te kry." Wanneer ons x bereken het, het ons ook ons antwoord gevind.
Metode 3 van 3: Verstaan die konsep

1. Wat presies is `n verwagtingswaarde?. Die verwagtingswaarde is nie noodwendig die resultaat wat die ooglopendste of logiesste is nie. Soms kan `n verwagtingswaarde selfs `n onmoontlike waarde in `n gegewe situasie wees. Byvoorbeeld, die verwagte waarde kan +$5 wees vir `n speletjie met `n prys van nie meer as $10 nie. Wat die verwagtingswaarde aandui, is hoeveel waarde `n bepaalde gebeurtenis het. As `n speletjie `n verwagte waarde van +$5 het, kan jy dit speel as jy voel dit is die tyd en geld werd wat jy per wedstryd kan kry. As `n ander speletjie `n verwagte waarde van -$20 het, sal jy dit net speel as jy dink elke speletjie is die $20 werd.

2. Verstaan die konsep van onafhanklike gebeurtenisse. In die alledaagse lewe dink baie van ons ons het `n gelukkige dag wanneer `n paar goeie dinge gebeur, en ons verwag dat die res van die dag dieselfde sal wees. Net so kan ons dink dat ons al genoeg ongelukke gehad het voor dan en dat iets regtig lekker nou moet gebeur. Wiskundig werk dinge nie so uit nie. As jy `n gewone muntstuk gooi, is daar presies dieselfde kans dat jy `n kop of `n muntstuk sal gooi. Dit maak nie saak hoeveel keer jy gegooi het nie; volgende keer as jy gooi werk dit nog steeds op dieselfde manier. Om die muntstuk te gooi is "onafhanklik" van die ander rolverdelings word dit nie daardeur geraak nie.

3. Verstaan die wet van groot getalle. Jy mag dalk dink dat die verwagtingswaarde nie regtig nuttig is nie, want dit vertel jou net selde wat die werklike uitkoms van `n situasie is. As jy bereken het dat die verwagte waarde van `n roulette-speletjie -€1 is, en jy speel 3 keer die speletjie, sal jy gewoonlik eindig met -€10, of +€60, of `n ander resultaat. Die "wet van groot getalle" help om te verduidelik hoekom die verwagtingswaarde nuttiger is as wat jy dalk dink: hoe meer gereeld jy speel, hoe nader aan die verwagtingswaarde sal die gemiddelde resultaat wees. As jy na die groot getalle gebeurtenisse kyk, is die kans groot dat die finale resultaat naby die verwagte waarde is.
Wenke
- Vir daardie situasies waar veelvuldige uitkomste moontlik is, kan jy `n sigblad in die rekenaar skep om die verwagtingswaarde uit die uitkomste en hul waarskynlikhede te bereken.
- Die €-berekeninge hierbo werk ook in ander geldeenhede.
Benodigdhede
- Potlood
- Papier
- Sakrekenaar
Artikels oor die onderwerp "Berekening van die verwagte waarde"
Оцените, пожалуйста статью
Soortgelyk
Gewilde