Memoriseer die eenheidsirkel: 14 stappe (met prente)

Inhoud

Trappe
- Deel 1 van 2: Onthou die radiale
- Deel 2 van 2: Onthou die x- en y-koördinate (kosinus, sinus)
Wenke

Om die eenheidsirkel te leer, sal jou nie net help met trigonometrie en meetkunde nie, maar ook met differensiaal- en integraalrekening. Dit lyk dalk na baie memorisering, maar sodra jy verstaan hoe dit werk, kan jy met `n paar nommers uit die eenheidsirkel begin en vinnig die res uitvind.

Trappe

Deel 1 van 2: Onthou die radiale

Prent getiteld Memoriseer die eenheidsirkel Stap 1

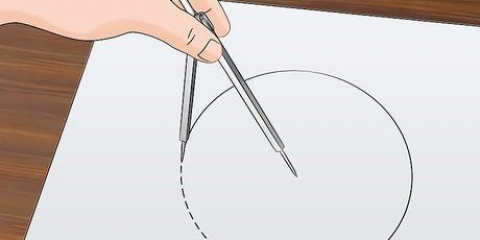
1. Trek twee loodregte lyne. Plaas `n kompas op `n groot vel papier. Trek `n vertikale en `n horisontale lyn. Hulle moet naby die middel van die bladsy sny. Dit is die x-as en y-as van die grafiek.

Prent getiteld Memoriseer die eenheidsirkel Stap 2

2. Trek `n sirkel. Gebruik `n kompas en teken `n groot sirkel wat gesentreer is by die kruising van die twee lyne.

Prent getiteld Memoriseer die eenheidsirkel Stap 3

3. Verstaan Radiale. `n Radiaal is `n hoekmaat. Dit word hoofsaaklik so gedefinieer dat `n persoon wat om `n sirkel loop met `n Ray van 1 eenheid beweeg deur `n hoek van `n radiaal nadat 1 eenheid om die omtrek geloop het. In die volgende stap sal ons die vier koördinaatpunte met die radiaalwaarde aandui. As jy die formule vir die verband tussen `n sirkel se omtrek en sy radius onthou, kan jy dit vinnig uitwerk, maar selfs al onthou jy dit nie.

Die radiaalmetings van die eenheidsirkel neem altyd aan dat jy by die punt (0, 1) begin. Om dit duidelik te maak na watter punt ons verwys, beskryf ons die sirkel as `n kompasroos:

Prent getiteld Memoriseer die eenheidsirkel Stap 4

4. Onthou dat die omtrek van die sirkel 2π is. Die omtrek van `n sirkel is gelyk aan 2πr, waardeur r staan vir die radius (die radius). Aangesien die eenheidsirkel `n radius van 1 het, kan ons die omtrek tot 2π vereenvoudig. Die radiaalwaarde van enige punt op die omtrek kan gevind word deur eenvoudig 2π te deel deur daardie deel van die sirkel wat jy gehad het. Dit is baie makliker as om elke enkele waarde op die sirkel te memoriseer.

Prent getiteld Memoriseer die eenheidsirkel Stap 5

5. Dui die vier punte op die x- en y-asse aan. Al wat jy hoef te doen is om 2π in kwarte te verdeel:

`Oos` is die beginpunt, so jy het 0 radiale gehad.

`Noord` = `n kwart van die omtrek van die sirkel = /₄ = /₂ radiale.

`Wes` = halfpad deur die sirkel = /₂ = π radiale.

`Suid` = driekwart van die sirkel = 2π * ¾ = /₂ radiale.

As jy oor die hele omtrek stap, keer jy terug na die beginpunt. Jy kan dit aandui as 2π of 0.

Prent getiteld Memoriseer die eenheidsirkel Stap 6

6. Verdeel die sirkel in agt stukke. Trek nou `n diagonale lyn deur elke kwadrant, perfek deur die middel. Weereens, gebruik deling om die waarde in radiale te vind:

/₄

(π/2, π, 3π/2 en 2π is reeds aangedui.)

Prent getiteld Memoriseer die eenheidsirkel Stap 7

7. Verdeel die sirkel in ses segmente. Trek nou bykomende lyne wat die sirkel in ses segmente verdeel. (Jy kan `n gradeboog hiervoor gebruik, begin by die positiewe x-as, waar elke segment 60 grade meet). Jy kan dieselfde benadering as hierbo gebruik om seker te maak een-sesde van `n sirkel is gelyk aan /₆ = /₃ radiale. Gebruik hierdie etiket vir die volgende punte op die omtrek (een in elke kwadrant):

/₃

(π en 2π is reeds aangedui)

Prent getiteld Memoriseer die eenheidsirkel Stap 8

8. Teken die twaalfdes daarin. Die laaste punte wat op die meeste eenheidsirkels gemerk is, dui inkremente van een twaalfde van die omtrek aan. Slegs vier hiervan is nog nie verklaar nie:

/₆

Deel 2 van 2: Onthou die x- en y-koördinate (kosinus, sinus)

Prent getiteld Memoriseer die eenheidsirkel Stap 9

1. Verstaan cosinus en sinus. Die eenheidsirkel is veral nuttig vir trigonometriese berekeninge met regte hoeke. Elke x-koördinaat van `n punt op die sirkel is gelyk aan cos(θ) en elke y-koördinaat is gelyk aan sin(θ), waar θ die waarde van die hoek is.

As jy dit moeilik vind om te onthou, dink aan (cos, sin) `omdat sinus laaste kom`.
Jy kan dit aflei deur reghoekige driehoeke en die definisie van hierdie funksies te gebruik — onthou `soscastoa`?

Prent getiteld Memoriseer die eenheidsirkel Stap 10

2. Skryf die koördinate by vier punte van die sirkel neer. `n `Eenheidsirkel` is bloot `n sirkel met `n radius van presies een eenheid. Gebruik dit om die x- en y-koördinate van die vier punte op die sirkel te vind waar dit `n as sny. (Ons noem dit `Oos`, `Noord`, ens. vir maklike lees, maar dit is nie amptelike name nie).

Die koördinate van `Oos` is (1, 0).

Die koördinate van `Noord` is (0, 1).

Die koördinate van `Wes` is (-1, 0).

Die koördinate van `Suid` is (0, -1).

Dit werk net soos `n normale grafiek. Jy behoort hierdie koördinate self te kan vind, sonder om dit te hoef te memoriseer.

Prent getiteld Memoriseer die eenheidsirkel Stap 11

3. Memoriseer die koördinate van die eerste kwadrant. Die eerste kwadrant is die boonste regterkantste kwart van die sirkel, waar beide die x-waardes as die y-waardes is positief. Dit is die enigste koördinate wat jy moet onthou:

Op /₆, is die koördinate ( $\frac{\sqrt{3}}{2}, \frac{1}{2}$ ${frac{{sqrt{3}}}{2}},{frac{1}{2}}$ ).

Op /₄, is die koördinate ( $\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}$ ${frac{{sqrt{2}}}{2}},{frac{{sqrt{2}}}{2}}$ ).

Op /₃, is die koördinate ( $\frac{1}{2}, \frac{\sqrt{3}}{2}$ ${frac{1}{2}},{frac{{sqrt{3}}}{2}}$ ).

Let daarop dat daar slegs drie tellers is. Beweeg jy in `n positiewe rigting (links na regs vir die x-waardes, van onder na bo vir die y-waardes), dan is die volgorde soos volg: 1 → √2 → √3.

Prent getiteld Memoriseer die eenheidsirkel Stap 12

4. Trek reguit lyne om die ander koördinate in te vul. As jy `n perfek vertikale of `n perfek horisontale lyn tussen twee punte kan trek, dan het hulle dieselfde absolute waarde as x- en y-koördinate. Met ander woorde, jy kan `n lyn van `n punt in die eerste kwadrante trek, dieselfde koördinate neerskryf waar jy land, en spasie regs daarvan laat vir die teken (+ of -).

Byvoorbeeld, jy kan `n horisontale lyn trek tussen /₃ en /₃. Aangesien die koördinate by die eerste punt (

\frac{1}{2}, \frac{\sqrt{3}}{2}

${frac{1}{2}},{frac{{sqrt{3}}}{2}}$ ), die koördinate van die tweede punt (?

\frac{1}{2}, ? \frac{\sqrt{3}}{2}

${frac{1}{2}},?{frac{{sqrt{3}}}{2}}$ ), waardeur `?` verteenwoordig `n plus- of minusteken (+ of -).

Hier is `n vinniger manier: Kontroleer die noemer van die radiale. Alle punte wat eindig op /3 het dieselfde absolute koördinate, net soos alle punte wat eindig op /4 en alle punte wat eindig op /6.

Prent getiteld Memoriseer die eenheidsirkel Stap 13

5. Gebruik simmetrie om uit te vind of die teken positief of negatief is. Daar is verskeie maniere om te onthou waar om die minustekens op die eenheidsirkel te plaas:

Dink aan fundamentele reëls vir kaarte. Bo die X-as die punte is positief, onder dit negatief. Links van die y is negatief, reg is positief.

Begin vanaf kwadrant 1 en trek lyne na ander punte. As die lyn de y-as kruis die y-waarde sal teken verander. As die lyn de X-as kruis, dan verander die x-waarde van teken.

Leer `All Students Test Calculus` (ASTC), antikloksgewys. Kwadrant 1 het aslegs positiewe waardes, Kwadrant 2 het slegs positiewe waardes sinus waardes, Kwadrant 3 het slegs positiewe tangens waardes, en Kwadrant 4 het slegs positiewe Cosine waardes.

Ongeag die metode wat jy kies, is die tekens (+, +) vir kwadrant 1, (-, +) vir kwadrant 2, (-, -) vir kwadrant 3 en (+,-) vir kwadrant 4.

Prent getiteld Memoriseer die eenheidsirkel Stap 14

6. Gaan jou werk na. Hier is die volledige lys koördinaatwaardes vir elke benoemde punt op die sirkel (nie die vier punte op die asse getel nie), kloksgewys. Onthou, jy behoort al hierdie waardes te kan vind deur net die punte van kwadrant 1 te memoriseer:

Kwadrant 1: (

\frac{\sqrt{3}}{2}, \frac{1}{2}

${frac{{sqrt{3}}}{2}},{frac{1}{2}}$ ); (

\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}

${frac{{sqrt{2}}}{2}},{frac{{sqrt{2}}}{2}}$ ); (

\frac{1}{2}, \frac{\sqrt{3}}{2}

${frac{1}{2}},{frac{{sqrt{3}}}{2}}$ ).

Kwadrant 2: (

- \frac{1}{2}, \frac{\sqrt{3}}{2}

$-{frac{1}{2}},{frac{{sqrt{3}}}{2}}$ ); (

- \frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}

$-{frac{{sqrt{2}}}{2}},{frac{{sqrt{2}}}{2}}$ ); (

- \frac{\sqrt{3}}{2}, \frac{1}{2}

$-{frac{{sqrt{3}}}{2}},{frac{1}{2}}$ )

Kwadrant 3: (

- \frac{\sqrt{3}}{2}, - \frac{1}{2}

$-{frac{{sqrt{3}}}{2}},-{frac{1}{2}}$ ); (

- \frac{\sqrt{2}}{2}, - \frac{\sqrt{2}}{2}

$-{frac{{sqrt{2}}}{2}},-{frac{{sqrt{2}}}{2}}$ ); (

- \frac{1}{2}, - \frac{\sqrt{3}}{2}

$-{frac{1}{2}},-{frac{{sqrt{3}}}{2}}$ )

Kwadrant 4: (

\frac{1}{2}, - \frac{\sqrt{3}}{2}

${frac{1}{2}},-{frac{{sqrt{3}}}{2}}$ ); (

\frac{\sqrt{2}}{2}, - \frac{\sqrt{2}}{2}

${frac{{sqrt{2}}}{2}},-{frac{{sqrt{2}}}{2}}$ ); (

\frac{\sqrt{3}}{2}, - \frac{1}{2}

${frac{{sqrt{3}}}{2}},-{frac{1}{2}}$ )

Wenke

As jy `n toets of repetisie oor die eenheidsirkel het, teken eers die sirkel op afvalpapier sodat jy dit as verwysing vir elke probleem kan gebruik.
Die proses sal aansienlik vinniger wees as jy baie oefen. In die toekoms sal jy dalk net die x- en y-asse hoef te sien om alles te onthou, of jy het dalk nie eers meer `n grafiek nodig nie.